Tema: VECTORES
Un segmento de recta queda determinado por sus puntos extremos. Si estos puntos están
dados en un cierto orden se dice que el segmento está orientado.
Definición: un vector es un segmento orientado.
En la recta r tomamos los puntos A y B. Consideremos a A como el origen y a B como
el estremo, entonces hemos definido el vector
AB
. El punto A se llama punto inicial y
el punto B punto final. La punta de la flecha se dibuja en el punto final.
Los vectores tienen tres elementos:
módulo: está dado por la longitud del segmento orientado,
dirección: está definida por la orientación de la recta que contiene el segmento,
esta orientación se define por medio del ángulo que la recta forma con el semieje
positivo de las x ,
sentido: indica cual es el origen y cual es el extremo final del segmento (punta de
la flecha)
Notación: un vector se define
por medio de sus puntos extremos, ambos escritos en mayúsculas, con una barra
en la parte superior, por ejemplo:
AB
(se lee vector AB)
por medio de una letra en minúscula con una barra en la parte superior, por
ejemplo:
v
(se lee vector v)
Es indistinta la notación que utilicemos:
Componentes de un vector
Las componentes de un vector son los segmentos que representan sus proyecciones
sobre los ejes coordenados cartesianos.
En el plano
2
R
:
Supongamos que tenemos el vector ABv , definido por sus puntos final e inicial cuyas
coordenadas son conocidas:
),(
yx
AAA
;
),(
yx
BBB
Las componentes del vector ABv son:
sobre el eje x
xxx
ABv
A
B
r
A
B
v
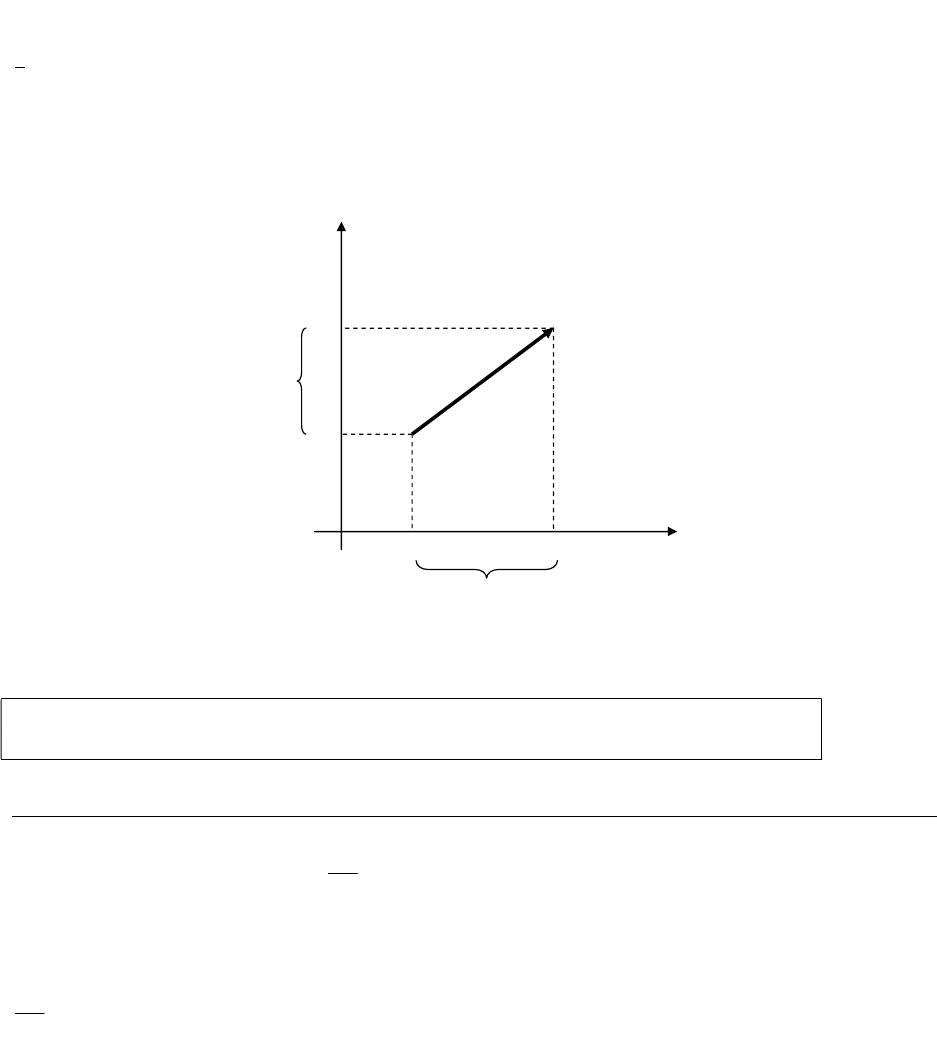
sobre el eje y
yyy
ABv
El vector en función de sus componentes, se puede escribir:
yyxxyx
ABABvvv ,),(
Resumiendo, las componentes de un vector se obtienen restando a las coordenadas de
su punto final, las coordenadas de su punto inicial.
Componentes del vector= coordenadas del punto final – coordenadas del
punto inicial
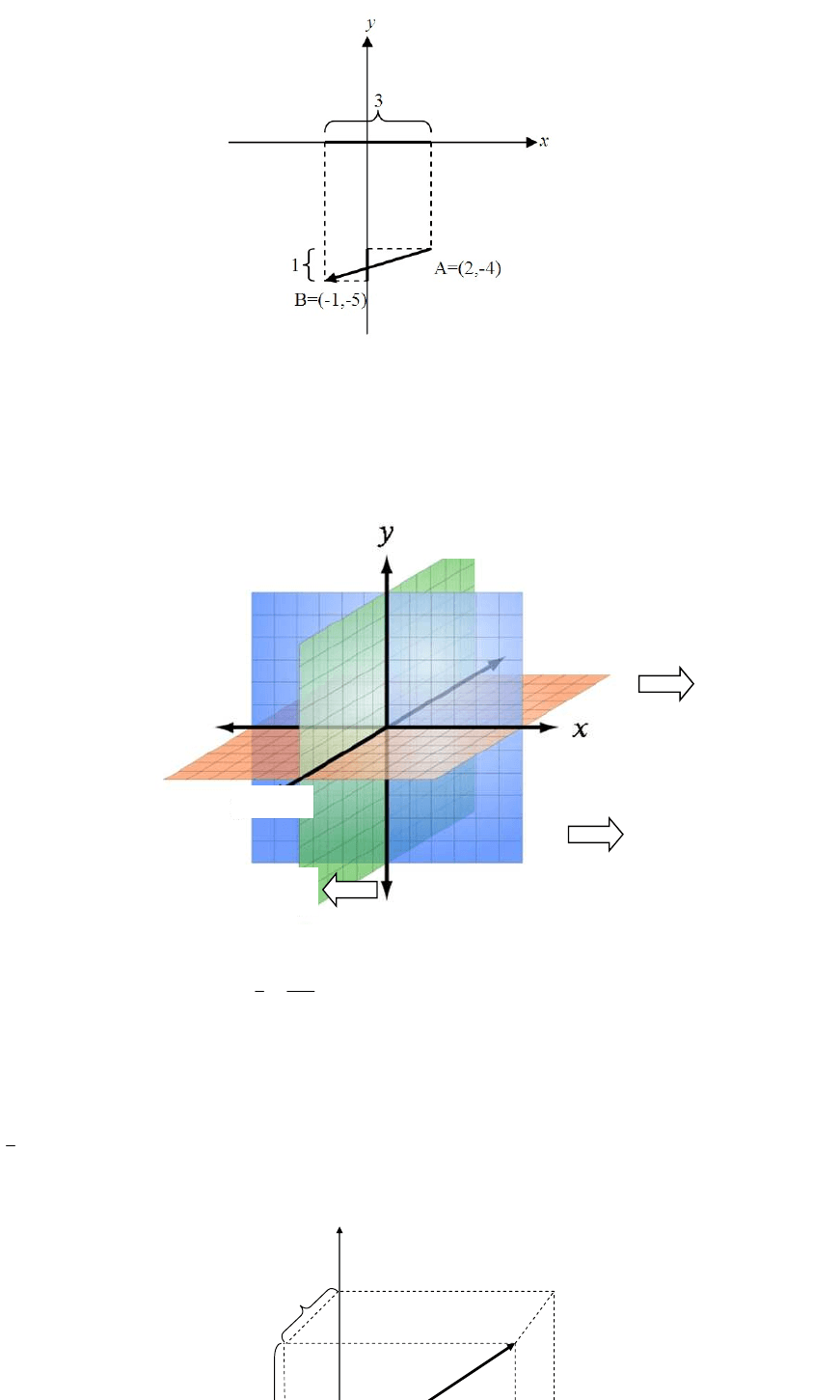
Ejemplo
Hallar las componentes del vector
AB
siendo
)5,1()4,2(
BA
.Graficar.
Para hallar las componentes del vector pedido haremos: coordenadas del punto final
menos coordenadas del punto inicial.
)1,3()4,2()5,1( ABAB
x
y
A
B
B
y
A
y
A
x
B
x
v
v
y
=
B
y
-
A
y
v
x
=
B
x
-
A
x
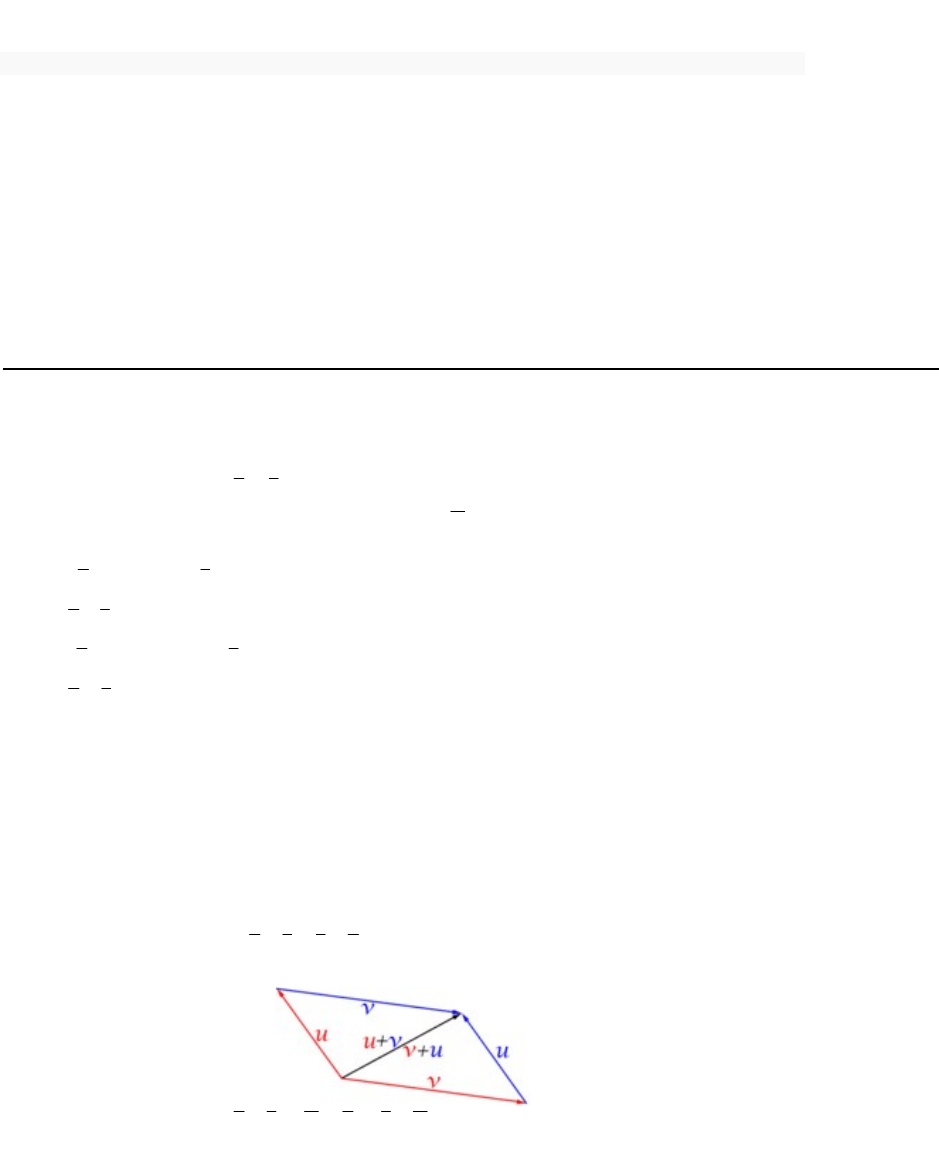
En el espacio
3
R :
Las componentes del vector
ABv
son:
sobre el eje x
xxx
ABv
sobre el eje y
yyy
ABv
sobre el eje z
zzz
ABv
El vector en función de sus componentes, se puede escribir:
zzyyxxzyx
ABABABvvvv ,,),,(
eje z
eje y
eje x
plano xz
plano yz
plano xy
el espacio
3
R
z
z
v
v
x
Operaciones entre vectores
Suma de vectores
La suma de dos vectores u y v es ley de composición interna, esto significa que si sumo
dos vectores obtengo como resultado otro vector w . Como los vectores se pueden
escribir en función de sus componentes, la suma puede definirse de esta manera:
En
2
R
, ),(
yx
uuu , ),(
yx
vvv
),(),(),(
yyxxyxyx
vuvuvvuuvu
En
3
R
, ),,(
zyx
uuuu , ),,(
zyx
vvvv
),,(),,(),,(
zzyyxxzyxzyx
vuvuvuvvvuuuvu
Las notaciones de arriba se leen: la suma de dos vectores es otro vector, cuyas
componentes son las sumas de las componentes homólogas de los vectores sumandos.
Componentes homólogas son las componentes que pertenecen a un mismo eje
coordenado.
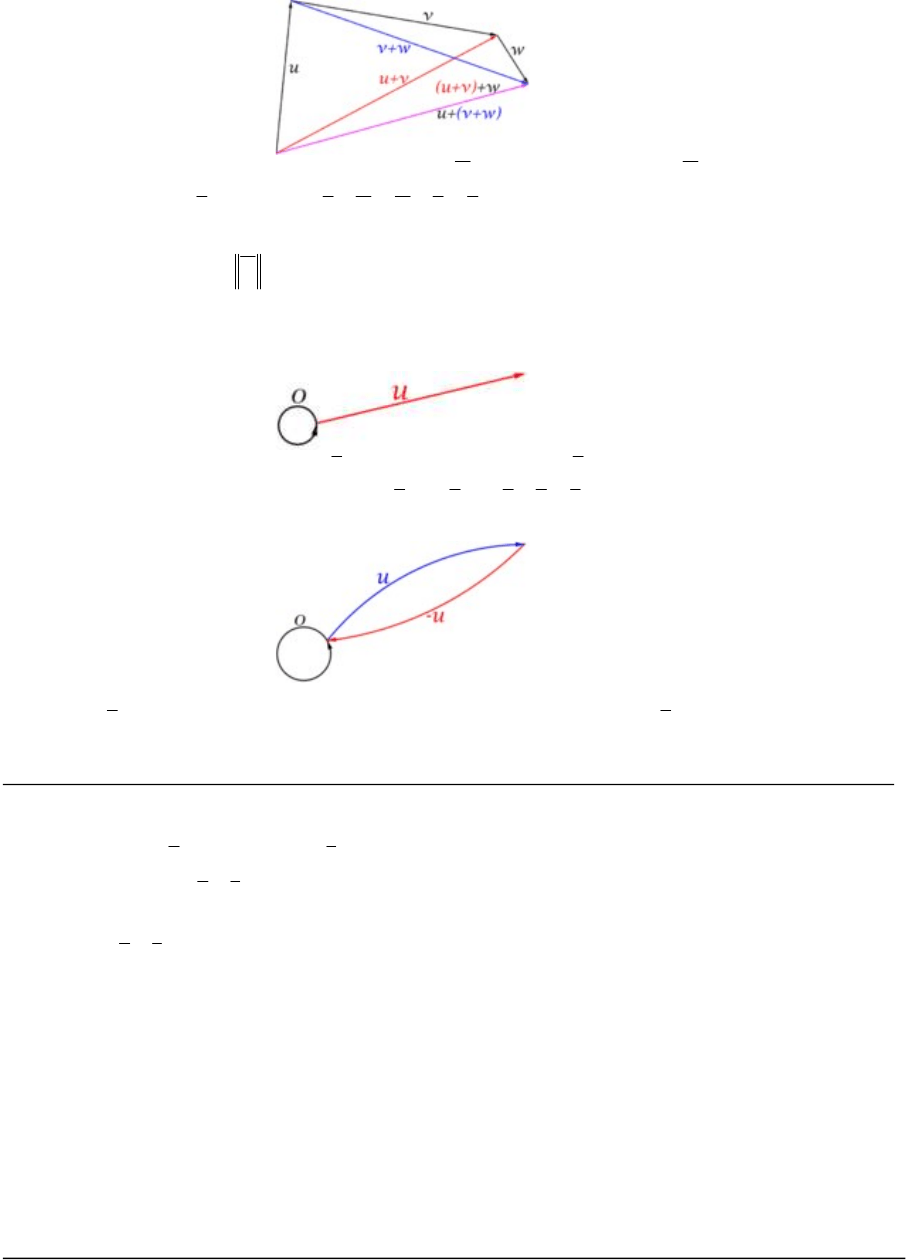
Gráficamente, la suma de dos vectores, se resuelve usando la regla del paralelogramo.
Propiedades de la suma de vectores
1. Propiedad conmutativa:
uvvu
2. Propiedad asociativa:
wvuwvu
3. Elemento neutro: es el vector nulo, en el plano
)0,0(O
y en el espacio
)0,0,0(O
,
para cualquier vector u , se cumple uuOOu .
El vector nulo se representa como un vector cuyo punto inicial coincide con el punto
final, su módulo es cero:
0O
.
Es un vector incapaz de efectuar, mediante la suma, modificación alguna a todos los
vectores.
4. Elemento opuesto: para el vector u su opuesto es el vector - u . La suma de ambos
vectores da como resultado el vector nulo:
0 uuuu
.
El vector - u tiene el mismo módulo y la misma dirección que el vector u , pero sentido
contrario.
Ejemplo
Sean los vectores
jkiu
ˆˆ
7
y
jiv
ˆ
3
ˆ
4
, hallar el valor de la componente k
para que se cumpla:
jivu
ˆ
5
ˆ
3
.
Partimos de
jivu
ˆ
5
ˆ
3
, es decir, del dato que es el vector suma de los dos vectores
dados, si reemplazamos queda:
jki
ˆˆ
7
+
ji
ˆ
3
ˆ
4
=
ji
ˆ
5
ˆ
3
si sumamos estos dos vectores, aplicando la definición
de suma queda:
jijki
ˆ
5
ˆ
3
ˆ
3
ˆ
47
Como dos vectores son iguales si lo son sus componentes homólogas, podemos afirmar
que:
853
33
kk
Producto de un vector por un escalar
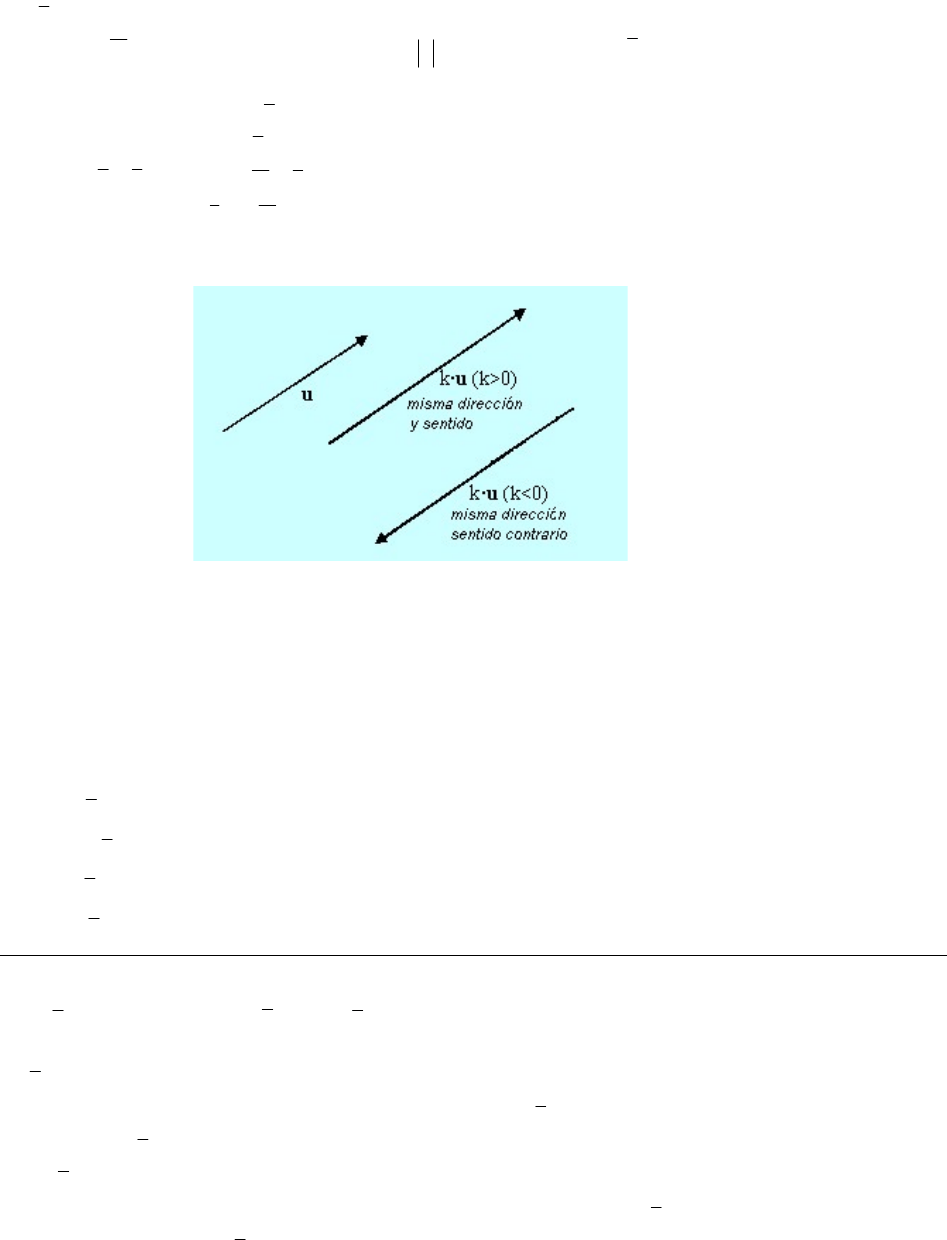
Si u es un vector no nulo y k es un número real (escalar) diferente de cero, entonces el
producto
uk.
es otro vector, cuyo módulo es
k
veces la longitud de
u y cuya dirección
es:
la misma que la de u , si 0
k y
es opuesta a la de u si 0
k .
Si k=0 o 0u se define
0. uk
El módulo del vector
ukv .
, es el producto del escalar por el módulo del vector, su
dirección es igual a la del vector, y su sentido es contrario a este, si el escalar es
negativo.
El producto de un vector por un escalar es ley de composición externa, esto significa
que necesito dos conjuntos, uno que contiene los escalares (cuerpo de los números
reales) y otro que contiene los vectores. El cuerpo real presta sus escalares al conjunto
de los vectores, para poder hacer esta operación, el resultado final cae dentro del
conjunto de los vectores.
Como los vectores se pueden escribir en función de sus componentes, el producto de un
vector por un escalar puede definirse de esta manera:
En
2
R
, ),(
yx
uuu
).,.(.
yx
ukukuk
En
3
R
, ),,(
zyx
uuuu ,
).,.,.(
zyx
ukukukuk
Ejemplo
Sea
1,2,3u
calcular
u.3 y
u).2(
analítica y gráficamente
)3,6,9()1,2,3.(3.3 u
obtuvimos un vector de la misma dirección y sentido que
u y cuyo módulo es 3 veces
el módulo de
u
)2,4,6()1,2,3).(2().2( u
obtuvimos un vector de la misma dirección pero sentido opuesto al de
u
y cuyo módulo
es 2 veces el módulo de
u
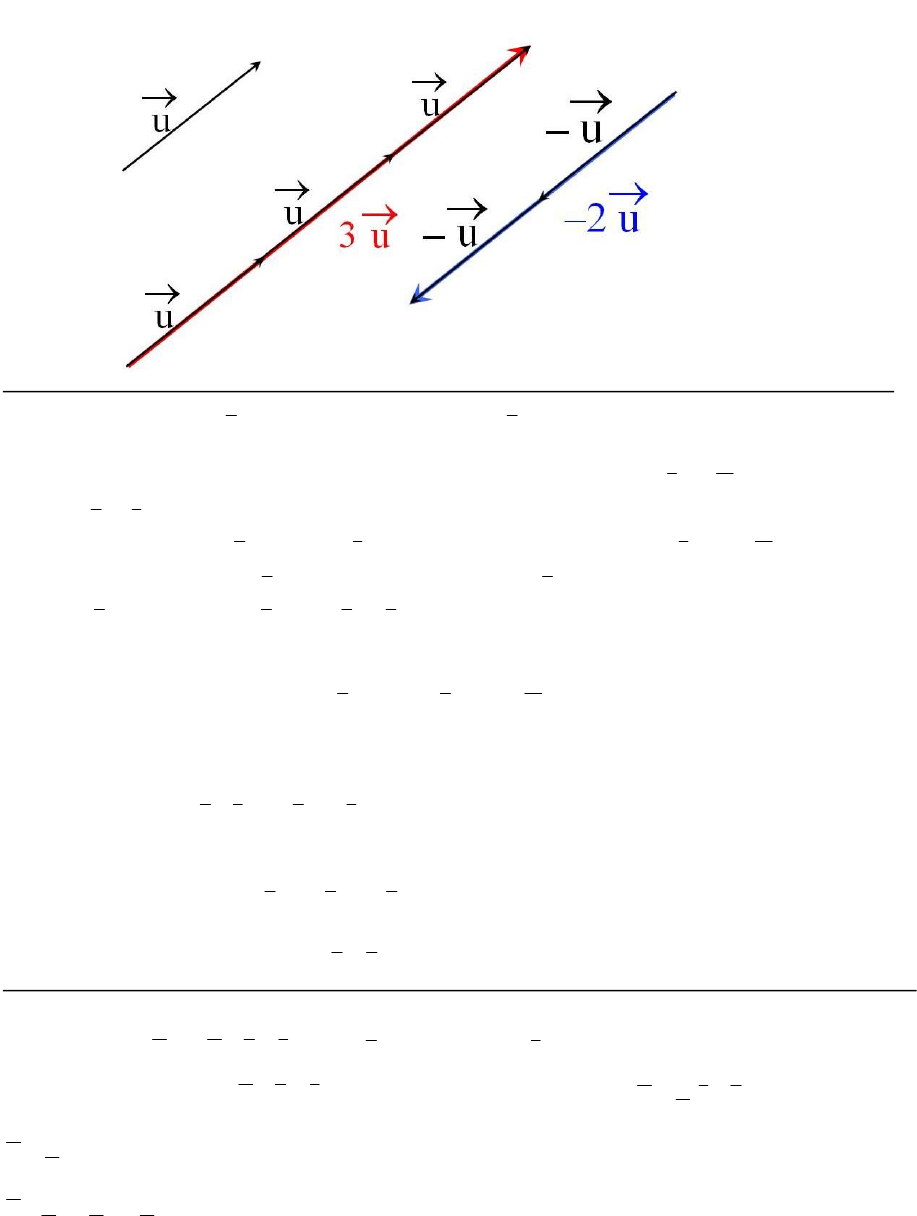
Un vector de la forma uk. se llama múltiplo escalar de u . En la figura superior se
observa que los vectores que son múltiplos escalares entre sí son paralelos.
Esta operación nos da la condición de paralelismo entre dos vectores: si
ukv .
entonces u y v son vectores paralelos.
Por ejemplo los vectores
)3,2,1(u
y
)9,6,3( v
son paralelos ya que
uv ).3(
Observar que el vector (-1). u tiene la misma longitud que u , pero sentido contrario.
Así (-1). u es el opuesto de u , (-1). u = - u .
Propiedades del producto de un vector por un escalar
1. Propiedad asociativa mixta:
vector
vector
vector
escalar
vector
vector
ukkukkukk ......
122121
2. Propiedad distributiva del producto de un vector por un escalar con respecto a la
suma de vectores:
vkukvuk ...
3. Propiedad distributiva del producto de un vector por un escalar con respecto a la
suma de escalares:
ukukukk ...
2121
4. Elemento neutro: es el número 1 , cualquier vector multiplicado por el número 1 da
como resultado el mismo vector
uu .1
Ejemplo
Hallar el vector w si vuw 2 siendo
kjiu
ˆ
5
ˆ
3
ˆ
y
kjv
ˆ
4
ˆ
2
Partimos de la ecuación
vuw 2 reemplazando y operando queda:
uvw
2
1
2
1
w
kjikj
ˆ
5
ˆ
3
ˆ
ˆ
4
ˆ
2
w =
kji
ˆ
2
9
ˆ
2
1
ˆ
2
1
Versores
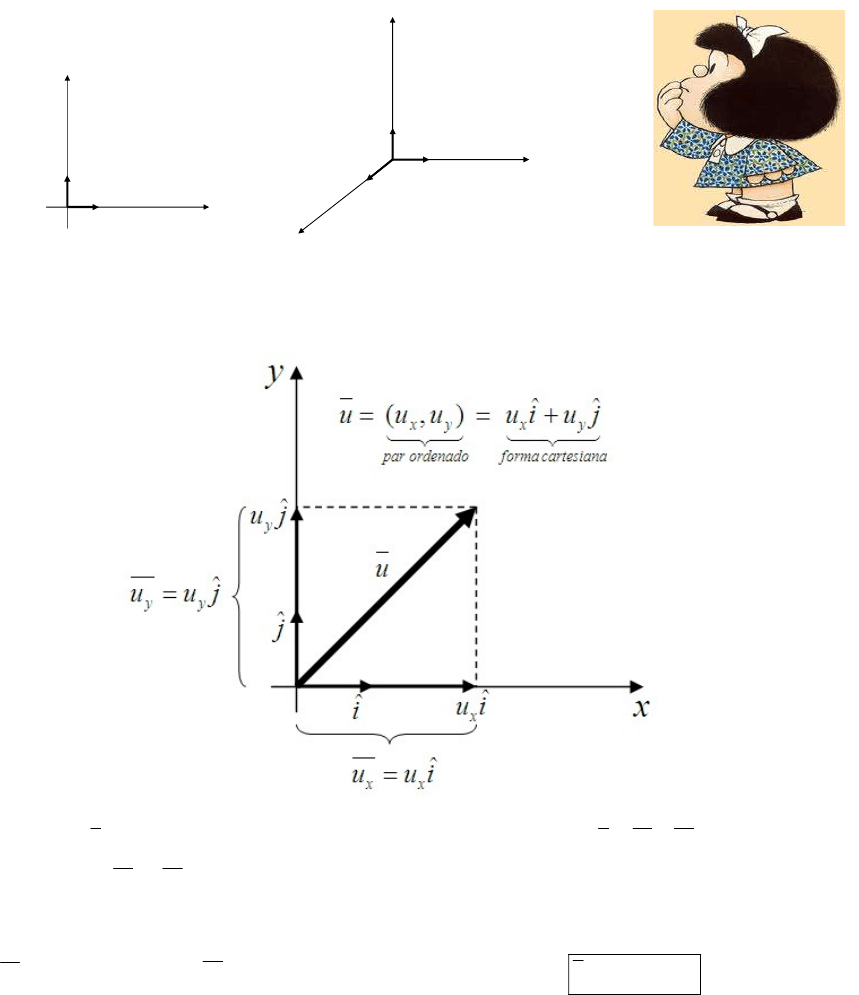
Los versores son vectores que tienen las siguientes características:
módulo unitario, esto significa que la longitud del segmento mide 1,
dirección y sentido coinciden con las direcciones y sentidos de los semiejes
coordenados cartesianos positivos
En el plano se designan por
ji
ˆ
,
ˆ
, cuyas componentes son
)1,0(
ˆ
,)0,1(
ˆ
ji
, y en el
espacio
kji
ˆ
,
ˆ
,
ˆ
, cuyas componentes son
)1,0,0(
ˆ
,)0,1,0(
ˆ
,)0,0,1(
ˆ
kji
.
Todo vector del plano o del espacio puede expresarse en función de los versores.
Al vector
u lo puedo pensar como el vector resultante de la suma
yx
uuu . A su vez
los vectores
x
u y
y
u
los puedo escribir como el producto entre un escalar (componente)
y un vector (versor) :
vector
escalar
xx
iuu
ˆ
.
;
vector
escalar
yy
juu
ˆ
. reemplazando nos queda:
juiuu
yx
ˆ
.
ˆ
.
esta es la
expresión cartesiana de un vector en el plano.
j
ˆ
i
ˆ
x
y
x
y
i
ˆ
j
ˆ
k
ˆ
k
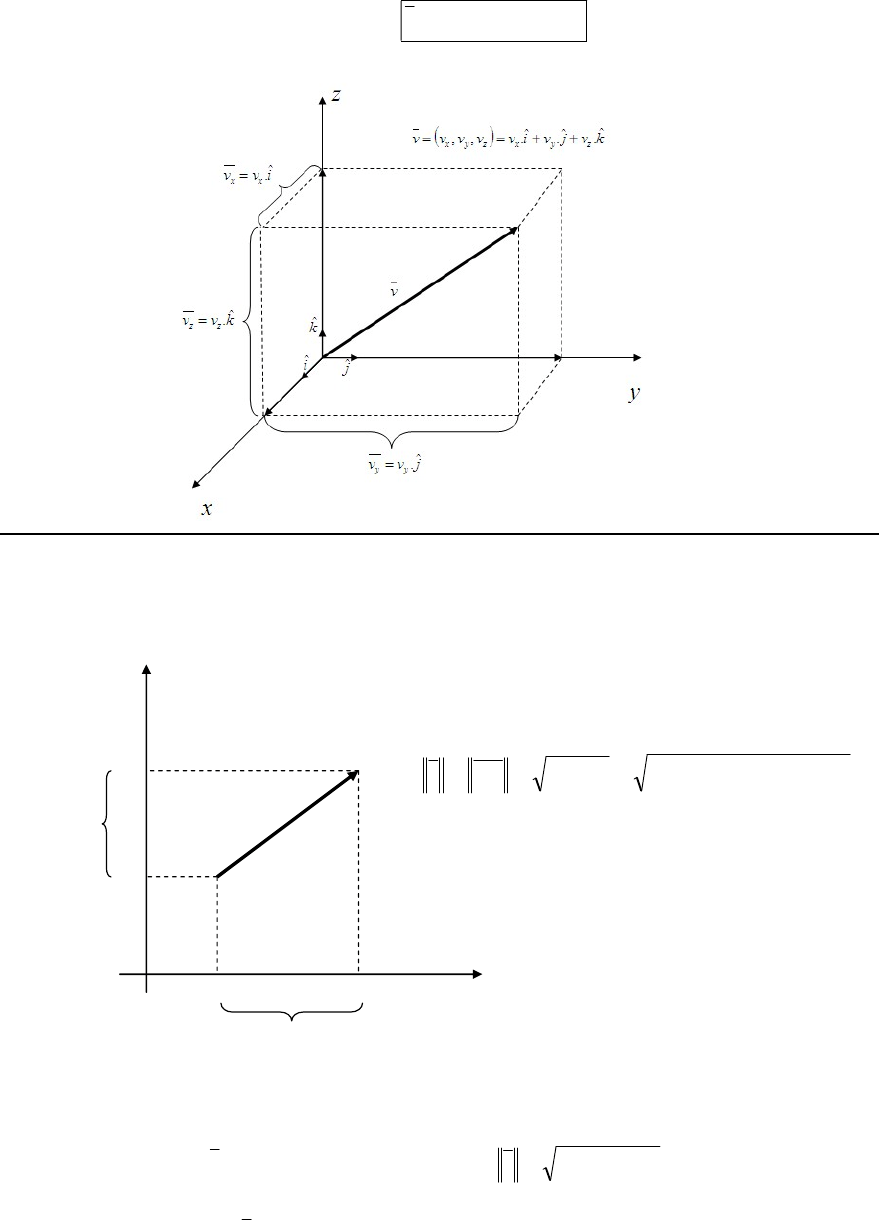
En el espacio el razonamiento es análogo:
kvjvivv
zyx
ˆ
.
ˆ
.
ˆ
.
Módulo de un vector
El módulo de un vector es la longitud del segmento que lo representa. Si el vector está
en el plano su módulo se calcula aplicando el teorema de Pitágoras:
En el espacio se calcula con el siguiente teorema:
Teorema
El módulo del vector
),,(
zyx
vvvv
del espacio
3
R
es
222
zyx
vvvv
.
Demostración:
Representemos al vector
),,(
zyx
vvvv del espacio
3
R
con punto inicial en O y punto
final en P. Vemos en la figura que se forman dos triángulos rectángulos
BAO
y
PBO
.
x
y
A
B
B
y
A
y
A
x
B
x
v
v
y
=
B
y
-
A
y
v
x
=
B
x
-
A
x
22
22
yyxxyx
ABABvvABv
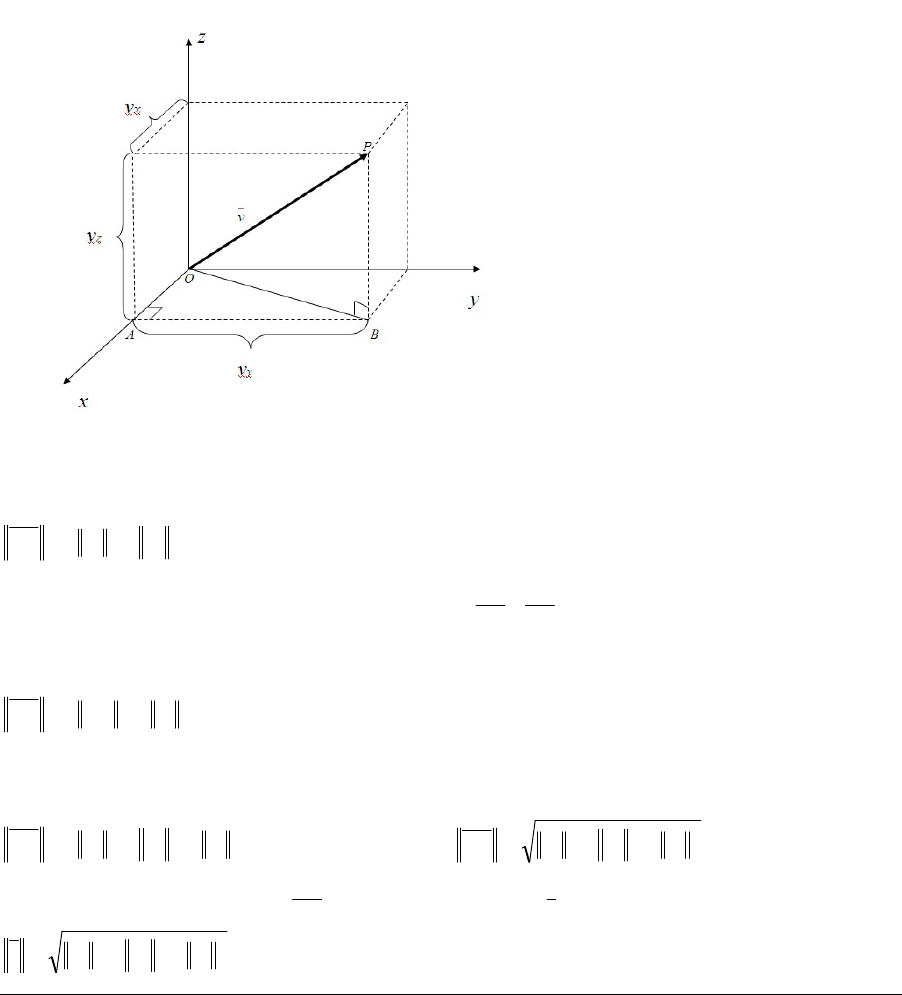
En el triángulo
BAO
, la hipotenusa es el segmento
OB ,
x
v y
y
v
son los catetos,
podemos aplicar el teorema de Pitágoras:
2
2
2
yx
vvOB (1)
En el triángulo
PBO
, la hipotenusa es el segmento
OP , OB y
z
v son los catetos,
podemos aplicar otra vez el teorema de Pitágoras:
22
2
z
vOBOP (2)
Si reemplazamos la expresión (1) en la (2) queda:
2
2
2
2
zyx
vvvOP
o lo que es lo mismo:
2
2
2
zyx
vvvOP
Como la longitud del segmento
OP es el módulo del vector v , se cumple:
2
2
2
zyx
vvvv
Una de las aplicaciones que tiene este tema y que utilizaremos mas adelante, cuando
veamos recta y plano, es que permite hallar la distancia entre dos puntos.
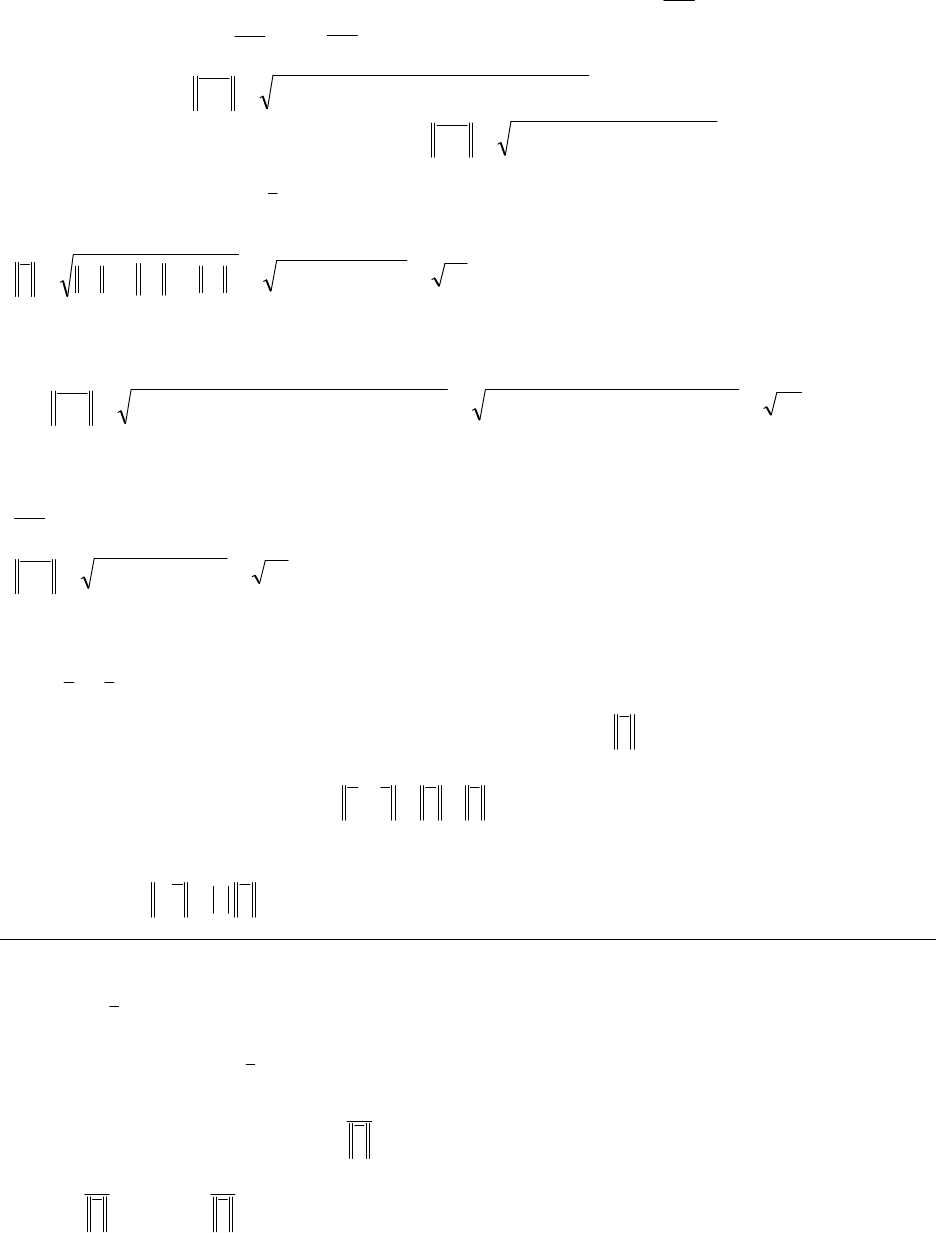
Supongamos que
),,(
zyx
PPPP
y
),,(
zyx
QQQQ
son dos puntos en el espacio
tridimensional, entonces la distancia entre ellos es el módulo del vector
PQ
. Las
componentes del vector
PQ
son:
),,(
zzyyxx
PQPQPQPQ , aplicando el teorema
ya visto queda:
222
)()()(
zzyyxx
PQPQPQPQd
.
Si los puntos estuvieran en el plano seria:
22
)()(
yyxx
PQPQPQd
Ejemplo
Hallar el módulo del vector
)1,2,3(v
1412)3(
222
2
2
2
zyx
vvvv
Hallar la distancia entre los puntos
)5,1,2(
P
y
)1,3,4(
Q
44)51()13()24()()()(
222222
zzyyxx
PQPQPQPQd
Hallar el módulo del vector con punto inicial
)2,1,1(
P
y extremo en
)4,5,0(
Q
)2,6,1()24,15,10(),,(
zzyyxx
PQPQPQPQ
4126)1(
222
PQ
Propiedades del módulo de un vector
Sean
u y v dos vectores y k un escalar, entonces:
1. El módulo de un vector es un número real positivo o nulo:
0v
.
2. El módulo de la suma de dos vectores es menor o igual a la suma de los módulos
de cada uno de los vectores:
vuvu
(Desigualdad del triángulo).
3. El módulo del vector que se obtiene mediante el producto de un escalar por un
vector, es igual al valor absoluto del escalar multiplicado por el módulo del
vector:
ukuk ..
Ángulos directores
Un vector
v del plano o del espacio, forma con los semiejes coordenados cartesianos
positivos ángulos, que se llaman ángulos directores. En la figura vemos que proyectar
ortogonalmente al vector
v sobre el eje z queda determinado el triángulo rectángulo
MPO
, donde se cumple que
v
v
z
cos
. De manera análoga, se deduce que:
v
v
x
cos
y
v
v
y
cos .
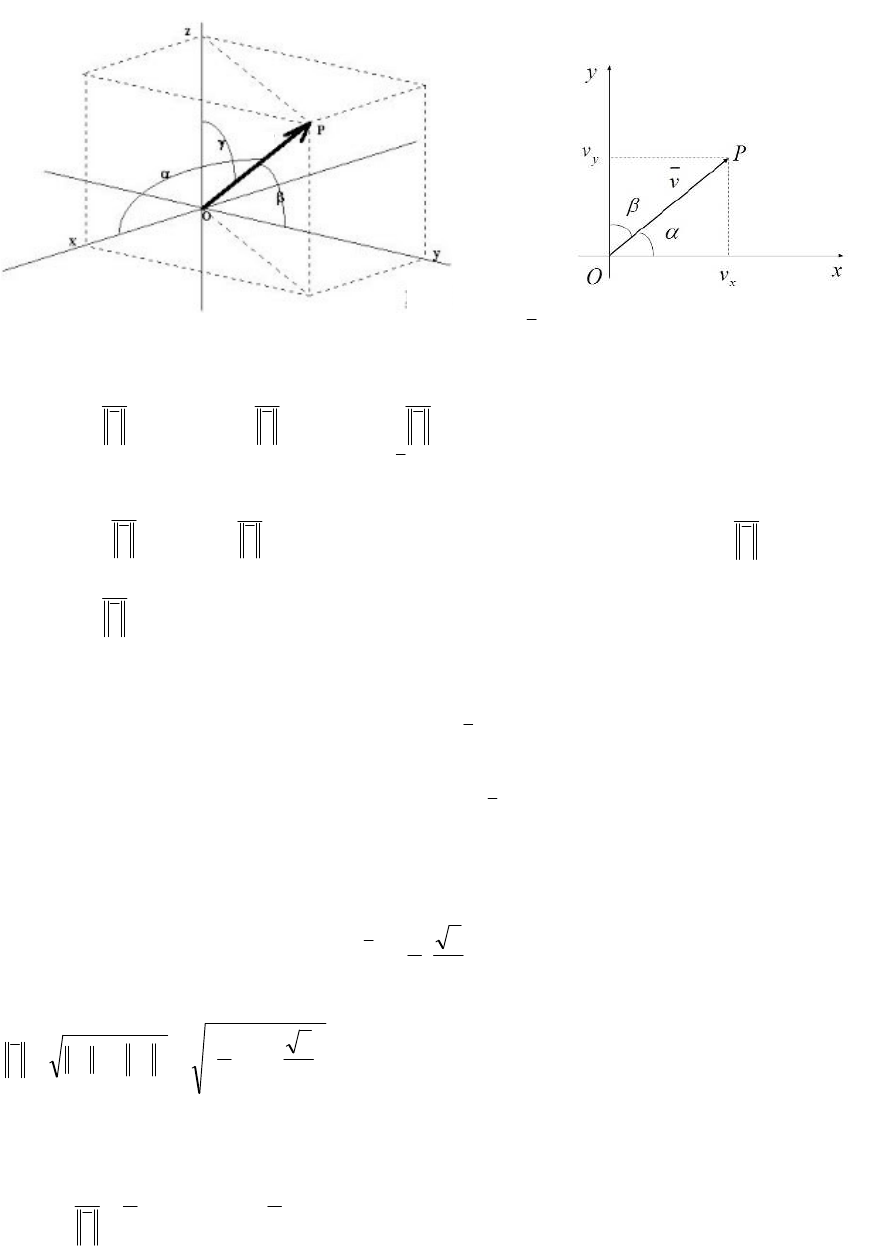
Estos valores se denominan cosenos directores del vector
v , y a partir de ellos se
deduce que los ángulos directores del vector son:
v
v
x
arccos
v
v
y
arccos
v
v
z
arccos
En el plano el razonamiento es similar, sea
),(
yx
vvv entonces los cosenos directores
son
v
v
x
cos
y
v
v
y
cos , por lo tanto los ángulos directores son:
v
v
x
arccos
y
v
v
y
arccos
.
Relación pitagórica
1. Sean
ˆ
y
ˆ
los ángulos directores de un vector ),(
yx
vvv del plano, entonces:
1coscos
22
.
2. Sean
ˆ
,
ˆ
y
ˆ
los ángulos directores de un vector
),,(
zyx
vvvv del espacio,
entonces:
1coscoscos
222
.
Ejemplo
Hallar los ángulos directores del vector
2
3
,
2
1
v
Primero calculamos el módulo del vector dato:
1
2
3
2
1
2
2
2
yx
vvv
El módulo de este vector vale 1, en este caso se le llama vector unitario.
º60
2
1
arccos
2
1
cos
v
v
x
M
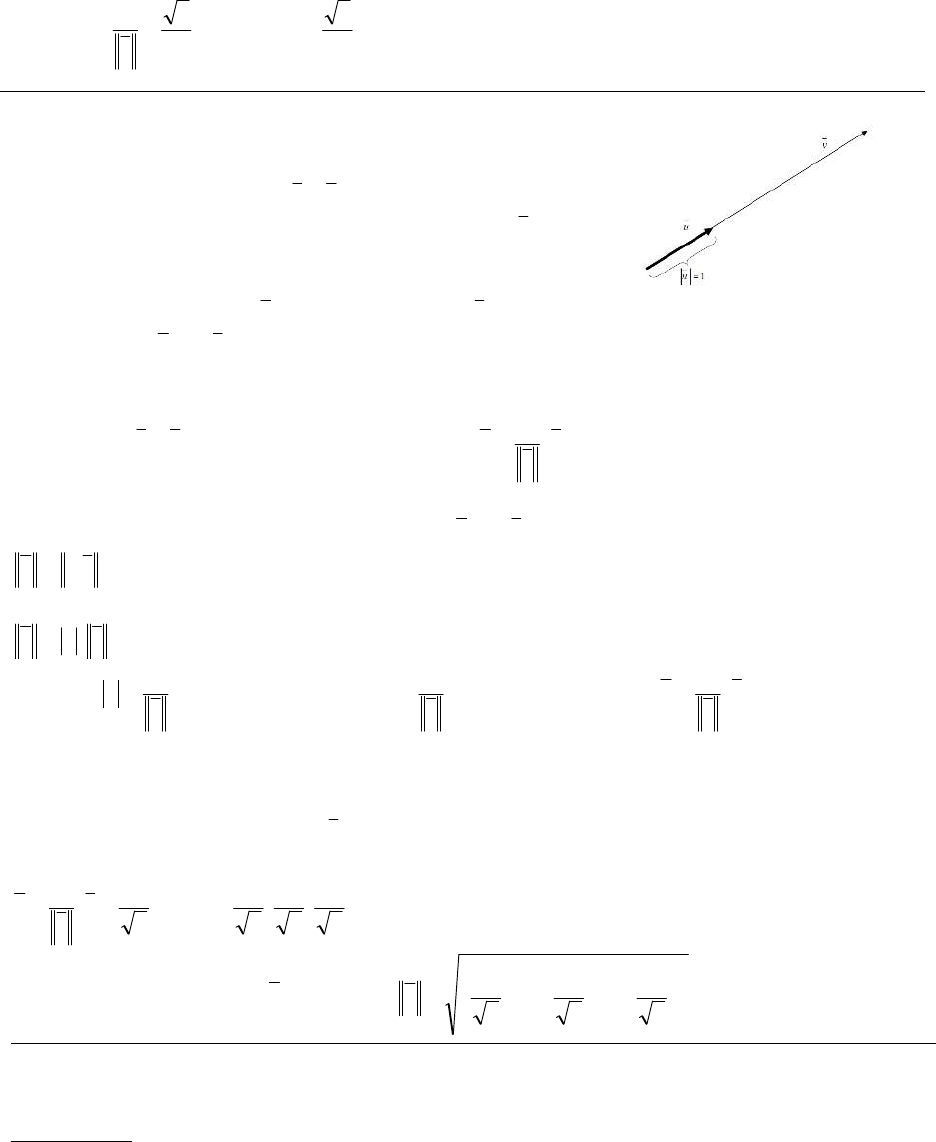
º30
2
3
arccos
2
3
arccos
v
v
y
Versor o vector unitario asociado a un vector
El versor asociado a un vector
0v cumple con:
1. tiene la misma dirección y sentido que el vector v
2. su módulo es igual a 1.
En consecuencia, el versor
u asociado a un vector v es un múltiplo escalar de este
vector; es decir
vku .
, siendo
0
k
.
Teorema
Sea el vector
0v
, entonces su versor asociado es
v
v
u .
1
.
Demostración
Por la definición de versor asociado se tiene que
vku .
, siendo 0
k , de modo que
1. vku
Que por propiedad del módulo del múltiplo escalar de un vector se `puede escribir
1. vku
.
Entonces
v
k
1
y, como 0
k , resulta
v
k
1
, reemplazando queda:
v
v
u .
1
.
Ejemplo
Hallar el versor asociado al vector
)1,1,1(v
3
1
,
3
1
,
3
1
)1,1,1(
3
1
.
1
v
v
u
Si calculamos el módulo de
u
se verifica :
1
3
1
3
1
3
1
2
22
u
EJERCITACION
Ejercicio Nº1
Hallar las componentes y el módulo de un vector, con punto inicial P:(3,2,0) y punto
final F:(1,0,0).
Este ejercicio da como datos dos puntos: P:(3,2,0) y F:(1,0,0) y pide las componentes
y el módulo del vector cuyos puntos inicial y final son los puntos P y F.
Recordemos que las componentes de un vector son sus proyecciones sobre los ejes
coordenados, como este vector está en el espacio, tendrá tres componentes, una sobre
cada eje.
Para hallar las componentes del vector pedido haremos: coordenadas del punto final
menos coordenadas del punto inicial.
Componentes del vector:
coordenadas del punto final – coordenadas del punto inicial
Consideremos el vector
PF
, el punto inicial es P y el punto final es F.
)0,2,2()0,2,3()0,0,1(),,(),,(
zyxzyx
PPPFFFPFPF
Las componentes del vector se pueden escribir en forma de terna ordenada de esta
manera:
)0,2,2( PF
o en forma cartesiana utilizando los versores
kji
ˆ
,
ˆ
,
ˆ
. Por lo que
el vector también se puede expresar así:
kjiPF
ˆ
0
ˆ
2
ˆ
2
.
El vector se puede nombrar usando el punto inicial seguido por el punto final, con un
segmento en la parte superior, de esta forma:
PF
, aquí el punto inicial es P y el final es
F. Otra forma de nombrar al mismo vector, es usando una letra minúscula con un
segmento en la parte superior, de esta forma: v .
kjiv
ˆ
0
ˆ
2
ˆ
2
F punto final
PFv
P punto inicial
Para hallar el módulo del vector
PFv , es decir la longitud del segmento que lo
representa, aplicamos el teorema de Pitágoras en el espacio:
80)2()2()()()(
222222
zzyyxx
PFPFPFPFv
Rta:
kjiv
ˆ
0
ˆ
2
ˆ
2
8v
Componentes
Punto inicial
Punto final
Ejercicio Nº2
Hallar las componentes y el módulo de un vector, con punto inicial P=(0,0,0) y punto
final
F= (-1,-1,3).
Idem ejercicio Nº 1;
Conclusión: el vector encontrado es el vector posición del punto F. El vector nulo es el
vector posición del origen de coordenadas
)0,0,0(O
Ejercicio Nº3
Dadas las componentes
zyx
vvv ,,
de un vector
v y su punto inicial P, encontrar el punto
final F.
Datos:
0,1,2
zyx
vvv
, P:(2,1,-3)
Recordando:
Componentes del vector: coordenadas del punto final – coordenadas del punto inicial
Podemos deducir despejando que:
Coordenadas del punto final: Componentes del vector+ coordenadas del punto inicial
Reemplazando en la ecuación obtenida por los datos queda:
)3,2,4()3,1,2()0,1,2(),,(),,(),,(
zyxzyxzyx
PPPvvvFFF
Rta: F= (4,2,-3)
Ejercicio Nº4
Dado el vector
)1,2,1( v
; a) Hallar el punto final F del mismo si su punto inicial es
)1,1,1(
P
b) Utilizando el mismo vector
v , encontrar las coordenadas del punto
inicial P si su punto final es
)2,2,3(
F
.
Similar al ejercicio Nº3
Ejercicio Nº5
Hallar un vector con sentido opuesto al de
)1,4,2( v
y que tenga el punto final F =
(2,0,-7)
Para hallar un vector con sentido opuesto al del vector
v , debemos multiplicar el vector
dado por el número (-1). Gráficamente:
Este documento contiene más páginas...
Descargar Completo
Vectores-Teórico.pdf
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.