Ejercicios Resueltos Unidad 2 (Parte 1) Prof. Ing. Natalia Montalván
1
Unidad 2 (Parte1): Ejercicios resueltos de la guía de trabajos prácticos
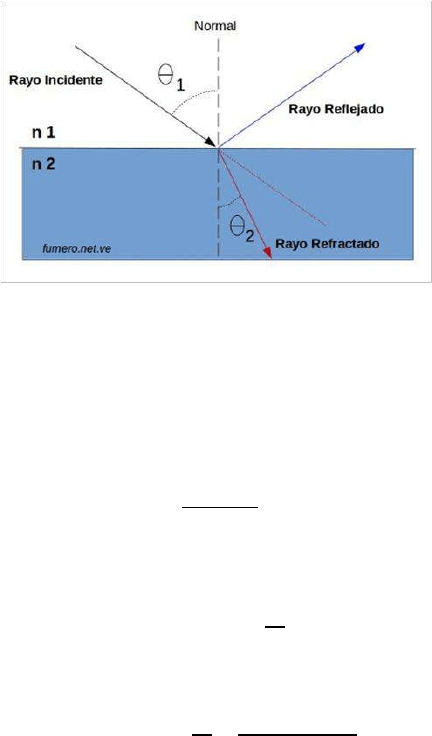
Ejercicio 7. Un rayo de luz incide sobre la superficie de un vidrio rodeada de aire, de índice de refracción n
vidrio
= 1,50,
con un ángulo de 50° con respecto a la normal. (a) Determinar las direcciones de los rayos reflejado y retractado y (b)
calcular la velocidad de ese rayo de luz en el vidrio, considerando que en el aire la velocidad de la luz es de 300000
km/s.
Solución: Primero debemos identificar la interface, en este caso el rayo pasa del aire al vidrio, por lo tanto n
1
=n
aire
=1 y
n
2
=n
vidrio
=1,50. Sabemos además que el ángulo de incidencia es de 50° medido siempre con respecto a la normal.
a) Dirección del rayo reflejado: es la misma que la dirección del rayo incidente, por lo tanto θ
R
= θ
1
= 50°.
Dirección del rayo refractado: planteamos la ley de Snell para la interface, reemplazamos los valores que son
datos y despejamos el ángulo de refracción θ
2
:
1
sin
1
=
2
sin
2
1 sin 50 = 1,50 sin
2
arcsin
1 sin 50
1,50
=
2
2
= 30,7°
b) Velocidad del rayo refractado en el vidrio (v
2
), la calculamos usando el índice de refracción:
2
=
2
2
:
2
=
2
=
300000 /
1,50
2
= 200000 /
Ejercicio 8. Un rayo de luz que viaja inicialmente por el agua (n = 1,33) ingresa a una sustancia transparente incidiendo
sobre ella con un ángulo de 37° respecto a la normal. El rayo se refracta en la primera superficie de separación agua-
sustancia, con un ángulo de 25°. Calcule la velocidad de la luz en la sustancia.
Solución: Identificamos la interface, el rayo pasa desde el agua hacia una sustancia desconocida, por lo tanto
n
1
=n
agua
=1,33 y n
2
=n
sustancia
=?
Sabemos que el ángulo de incidencia es de 37° y que el ángulo de refracción es de 25°. Planteamos la ley de Snell para
la interface y despejamos el índice de refracción de la sustancia desconocida:
Ejercicios Resueltos Unidad 2 (Parte 1) Prof. Ing. Natalia Montalván
2
1
sin
1
=
2
sin
2
1,33 sin 37 =
2
sin 25
1,33 sin 37
sin 25
=
2
1,89 =
2
A partir del índice de refracción calculamos la velocidad de la luz en la sustancia:
2
=
2
2
:
2
=
2
=
300000 /
1,89
2
= 158399,88 /
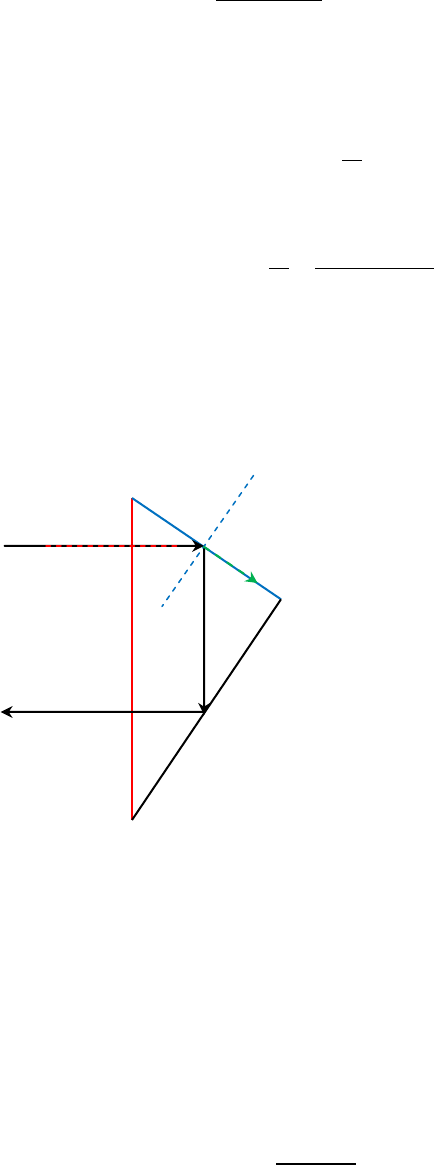
Ejercicio 9. Un rayo de luz incide perpendicularmente sobre la cara larga (la hipotenusa) de un prisma de 45° - 45° - 90°
rodeado por aire, como se muestra en la figura. Calcule el valor mínimo del índice de refracción del prisma, para el cual
el rayo seguirá la trayectoria mostrada en la figura.
Solución: El rayo incide perpendicularmente a la interface 1, por lo tanto el ángulo de incidencia es θ
1
=0° con respecto
a la normal N
1
y por lo tanto pasa por la interface 1 sin desviarse, siendo el ángulo del rayo refractado en la primer
interface θ
2
= 0. Al llegar a la interface 2 observamos que todo el haz de luz se refleja en la interface 2 y no la atraviesa,
este fenómeno se conoce como reflexión total interna. Llamaremos θ
1’
al ángulo crítico de incidencia sobre la interface
2 (por geometría podemos determinar que θ
1’
=45°) y θ
2’
=90° es el ángulo del rayo refractado. Planteamos la ley se Snell
en la interface 2 prisma-aire, llamamos n
2
=n
prisma
=? Y n
1
=n
aire
=1:
2
sin
1
=
1
sin
2
2
sin 45 = 1 sin 90
2
=
1 sin 90
sin 45
1,41 =
2
N
1
Rayo incidente 1
Interface 1:
aire-prisma
N
2
Interface 2: prisma-aire
Rayo refractado
θ
1’
Ejercicios Resueltos Unidad 2 (Parte 1) Prof. Ing. Natalia Montalván
3
Ejercicio 10. Determine la desviación d que experimenta un rayo de luz que incide con un ángulo de 30° sobre una
sustancia transparente de índice de refracción n = 1,52, de 1,00 cm de espesor y rodeada de aire.
Solución:
De la interface 1 calculamos el ángulo θ
2
aplicando la ley de Snell, considerando n
1
=aire y n
2
=sustancia:
1
sin
1
=
2
sin
2
1 sin 30 = 1,52 sin
2
arcsin
1 sin 30
1,52
=
2
2
= 19,2°
Ahora aplicamos la ley de Snell en la interface 2, considerando n
2
=sustancia y n
1
=aire. Observe que en este caso el
ángulo θ
1’
=θ
2
(son ángulos alternos internos).
2
sin
1
=
1
sin
2
1,52 sin 19,2 = 1 sin
2
arcsin
1,52 sin 19,2
1
=
3
2
= 30°
El ejercicio pide determinar la desviación d, del gráfico podemos observar que =
1
= 19,2° (son ángulos opuestos
por el vértice)
Finalmente: =
2
= 10,8°
Ejercicio 11. Determine el ángulo de desviación con que emerge un rayo de luz de un prisma de 30° rodeado de aire y
de índice de refracción n = 1,55.
Interface 2: sustancia-aire
Interface 1: aire-sustancia
θ
1
θ
2
θ
2’
d
N
1
N
2
θ
1’
β
30°
N
1
N
2
θ
1’
θ
2’
δ
60°
90
Interface 1: aire-prisma
Interface 2: prisma-aire
β
Ejercicios Resueltos Unidad 2 (Parte 1) Prof. Ing. Natalia Montalván
4
El ángulo de incidencia en la interface 1 aire-prisma es igual a cero, por lo cual el rayo atraviesa dicha interface sin
desviarse. Al llegar a la interface 2 prisma-aire debemos medir el ángulo de incidencia θ
1’
con respecto a la normal N
2
.
Del gráfico observamos en la normal N
2
que
1
= 90° 60° = 30°
Planteamos la ley de Snell en la segunda interface, siendo n
2
=n
prisma
y n
1
=n
aire
:
2
sin
1
=
1
sin
2
1,55 sin 30 = 1 sin
2
arcsin
1,55 sin 30
1
=
2
2
= 50,8°
El ejercicio pide la desviación δ, del gráfico podemos ver que =
1
= 30° (son ángulos opuestos por el vértice)
A su vez + =
2
Por lo tanto = 50,8° 30° = 20,8°
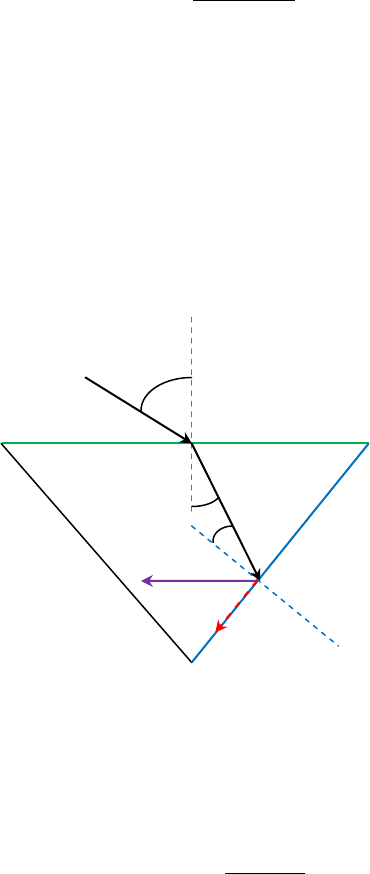
Ejercicio 12. El haz luminoso mostrado en la figura incide sobre la superficie 2 con el ángulo crítico. Determine el ángulo
de incidencia θ
1
. El prisma está rodeado de aire.
Comenzamos planteando la ley de Snell para la interface 2 (n
2
=n
prisma
y n
1
=n
aire
en esta interface el haz de luz va desde el
prisma hacia el aire), en la misma se produce el fenómeno de reflexión total interna, por lo que θ
1’
=θ
crítico
=42° (dicho
ángulo es dato, véase la guía de trabajos prácticos) y θ
2’
=90°.
2
sin
1
=
1
sin
2
2
sin 42 = 1 sin 90
2
=
1 sin 90
sin 42
1,49 =
2
Por geometría se puede determinar que el ángulo entre la normal N
1
y el haz refractado de la primera interface es
2
= 90° 72° = 18°
Habiendo calculado el índice de refracción del prisma y determinado el ángulo θ
2
, aplicamos la ley de Snell a la interface
1, siendo n
1
=n
aire
=1 y
n
2
=n
prisma
=1,49 (en este caso el haz de luz va desde el aire hacia el prisma)
N
1
Interface 1: aire-prisma
Interface 2: prisma- aire
N
2
θ
1
θ
2
θ
1’
Haz
reflejado
60°
48°
72°
42°
Ejercicios Resueltos Unidad 2 (Parte 1) Prof. Ing. Natalia Montalván
5
1
sin
1
=
2
sin
2
1 sin
1
= 1,49 sin
2
1
= arcsin
1,49 sin 18
1
1
= 27,4°
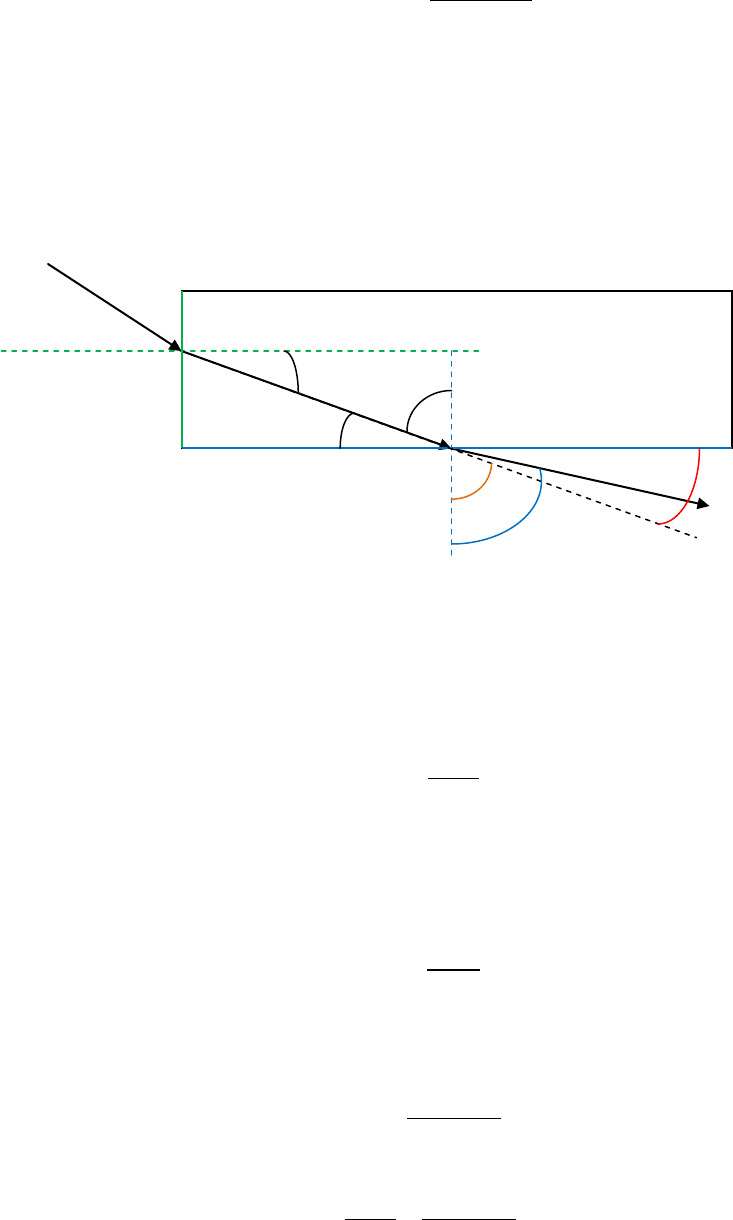
Ejercicio 13. Un rayo luminoso entra a un bloque rectangular de plástico con un ángulo de θ1 = 45,0° y emerge a un
ángulo de θ2’ =76,0°, como en la figura. a) Determine el índice de refracción del plástico. b) Si el rayo luminoso entra al
plástico en un punto L = 50,0 cm desde el borde del fondo, ¿Cuánto tarda el rayo luminoso en viajar a través del
plástico?
Ley de Snell para la interface 1:
1
sin
1
=
2
sin
2
1 sin 45 =
2
sin
2
2
=
sin 45
sin
2
Ley de Snell para la interface 2:
2
sin
1
=
1
sin
2
2
sin
1
= 1 sin 76
2
=
sin 76
sin
1
Del gráfico podemos observar que
2
+
1
= 90° por lo cual
1
= 90
2
Ecuación (3)
Reemplazamos θ
1’
en la ecuación (2)
2
=
sin 76
sin 90
2
Igualamos con la ecuación (1)
sin 45
sin
2
=
sin 76
sin 90
2
N
1
N
2
Interface 1: aire-bloque
Interface 2: bloque-aire
θ
1
θ
2’
θ
2
θ
1’
θ
2
θ
2
θ
1’
Ecuación (1)
Ecuación (2)
Ecuación (4)
Ejercicios Resueltos Unidad 2 (Parte 1) Prof. Ing. Natalia Montalván
6
Resolvemos la identidad trigonométrica para el seno de una resta:
sin 90
2
= sin 90 cos
2
cos 90 sin
2
= cos
2
Reemplazamos en la ecuación (4)
sin 45
sin
2
=
sin 76
cos
2
Reacomodamos la ecuación:
cos
2
sin
2
=
sin 76
sin 45
tan
2
=
sin 76
sin 45
2
= tan
1
sin 76
sin 45
2
= 36,1°
Reemplazamos el valor de θ
2
obtenido y calculamos el índice de refracción del bloque:
2
=
sin 45
sin 36,1
2
= 1.2
UNIDAD 3 Tiro oblicuo.pdf
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.