Volver a Estadística I
lOMoARcPSD|212725 42
Objetivo de aprendizaje:
Investigar la teoría y definición de conjuntos para conocer las características poder
identificarlos para tener conocimientos previos a la clase.
Teoría de Conjuntos
Antecedentes:
Georg Cantor (1845-1918) fue quien prácticamente formuló de manera individual la
teoría de conjuntos a finales del siglo XIX y principios del XX. Su objetivo era el de
formalizar las matemáticas como ya se había hecho con el cálculo cien años antes.
Cantor comenzó esta tarea por medio del análisis de las bases de las matemáticas y
explicó todo basándose en los conjuntos (por ejemplo, la definición de función se hace
estrictamente por medio de conjuntos).
El problema apareció cuando se comenzaron a encontrar paradojas en esta teoría,
siendo la más célebre la paradoja de Russell, y más tarde varios matemáticos
encontraron más paradojas, incluyendo al mismo cantor.
Russell descubrió su paradoja en 1901, y la publicó en un apéndice de su libro
"principios de las matemáticas". La primera propuesta para solucionar el problema de
las paradojas provino de un matemático holandés llamado Brouwer, quien propuso una
redefinición radical de todas las matemáticas y prometió una solución al conflicto.
En 1904 propuso la teoría de la prueba, la cuál era una teoría de la lógica independiente
del contexto y podría ser aplicada a las matemáticas sin encontrar paradojas. Russell a
su vez desarrolló su teoría de los tipos para evitar las paradojas. El proponía que los
enunciados se acomodaran jerárquicamente. Russell publicó sus resultados en1908
con la colaboración de Alfred North Whitehead. La cuarta respuesta a la paradoja fue
de Ernst Zermelo en 1908 con la axiomatización de la teoría de conjuntos
Definición:
Los conjuntos son un agregado o colección de objetos de cualquier naturaleza con
características bien definidas de manera que se puedan distinguir todos sus elementos.
A los objetos que lo componen se les llama elementos del conjunto.
lOMoARcPSD|212725 42
Un conjunto se denota con una letra mayúscula A, B, C y el elemento por una
letra minúscula a, b.
A los elementos se les encierra entre llaves ( {} ) y se separan por comas ( , ).
Según la cantidad de elementos que tenga un conjunto, éstos se pueden clasificar de
la siguiente manera:
Conjuntos Finitos
Son los que tienen un número conocido de elementos.
Ejemplos:
El conjunto de números que aparecen al lanzar un dado.
El conjunto de días de la semana.
Conjuntos Infinitos
Son lo que tienen un número ilimitado de elementos.
El conjunto de los números reales
El conjunto de los números reales entre 2 y 5
Conjunto universal
Es el conjunto de todos los elementos considerados en un problema o situación dada.
Ejemplos:
Si solo se desea trabajar con los números reales positivos, el conjunto universal
será U = R+ = (0, +∞)
Conjunto vacío
Un conjunto que no tiene elementos y se denota por ∅ ó { }
Ejemplos:
El conjunto A = {x ∈ ! / !!+ 1 = 0} es un conjunto vacío porque no hay ningún
número real que satisfaga !!+ 1 = 0.
El conjunto de los meses del año con 27 días.
Representación
Hay tres formas de representar los conjuntos, por medio del diagrama de Venn, por
extensión y por comprensión
lOMoARcPSD|212725 42
Extensión:
Es una representación escrita de los conjuntos cuando el conjunto y se utilizan las llaves
para hacerlo. Por ejemplo:
A= {Manzana, Mora, Fresa, Sandia, Banano, Naranja}
Básicamente, dice de forma escrita que: A es la representación de todas las frutas. Las
llaves cumplirían el papel bolsa donde están las frutas. Y la Manzana, Banano, Naranja
serían cada uno de los elementos que están conformando el conjunto.
Comprensión:
Es otra forma de representar los conjuntos de manera escrita y vas a encontrar algo
como esto:
A= {X / X frutas dentro de la bolsa}
Es una forma de abreviar la representación escrita de los conjuntos cuando están
conformados por demasiados elementos y se complica mencionar cada uno de ellos.
La expresión mencionada anteriormente se lee de la siguiente forma: "A es el conjunto
de los x tales que x es una fruta". Es decir, la x representa a cualquier elemento que
haga parte de conjunto, en este caso, serían muchas frutas. Cuando se hace alusión a
este tipo de representación de los conjuntos, solo se menciona la característica que
tienen en común y no a cada uno de los elementos que lo componen.
Diagramas de Venn
Cualquier figura geométrica cerrada (círculos, rectángulos, triángulos, óvalos, etc) sirve
para representar gráficamente las operaciones entre conjuntos, estos gráficos son
llamados Diagramas de Venn.
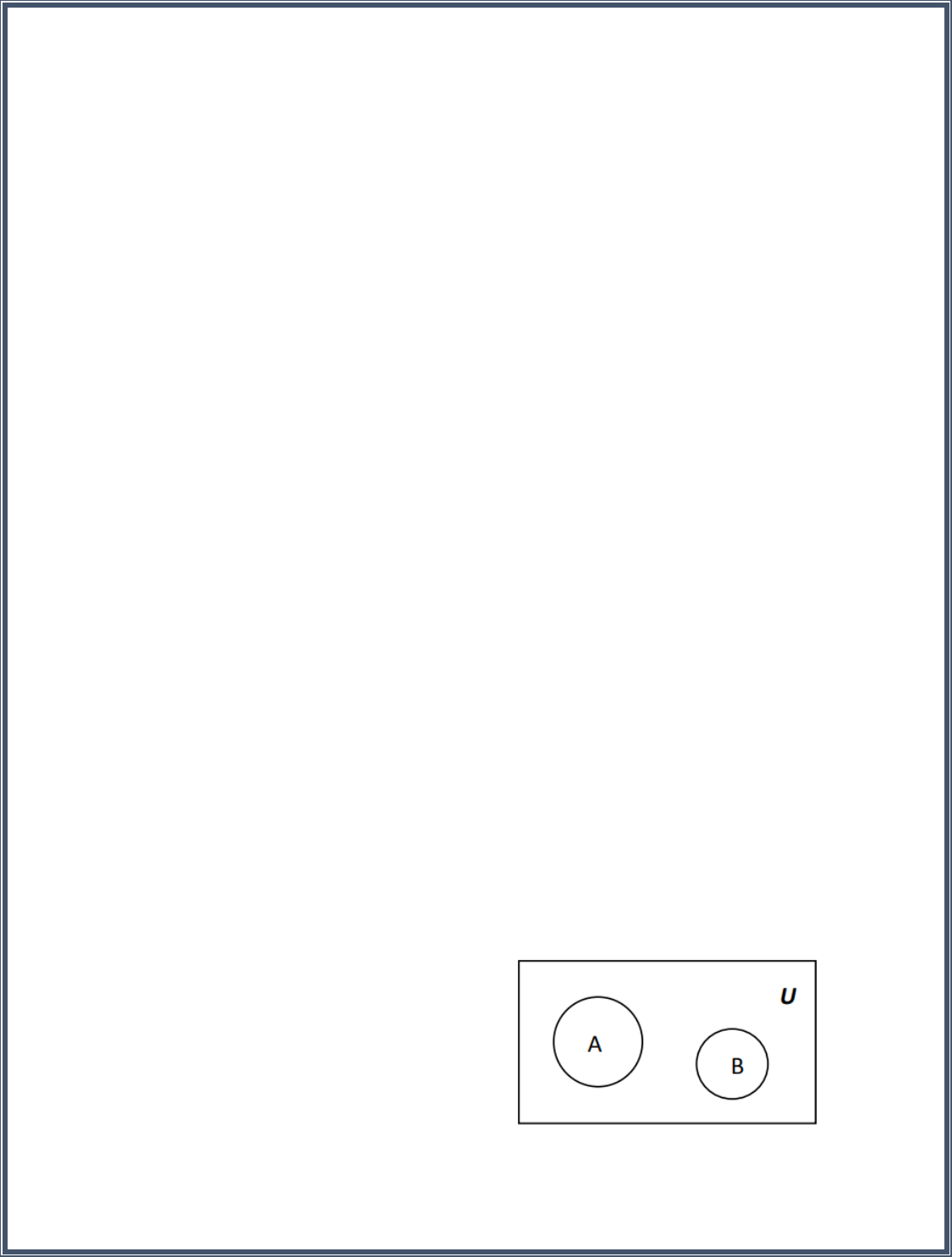
Normalmente, al conjunto universal se le
representa con un rectángulo y los conjuntos
con un círculo o elipse, tal y como se muestra
en la siguiente figura:
lOMoARcPSD|212725 42
Los diagramas de Venn en ningún momento constituyen una prueba matemática; sin
embargo, permiten tener una visión intuitiva de la relación que puede existir entre los
conjuntos.
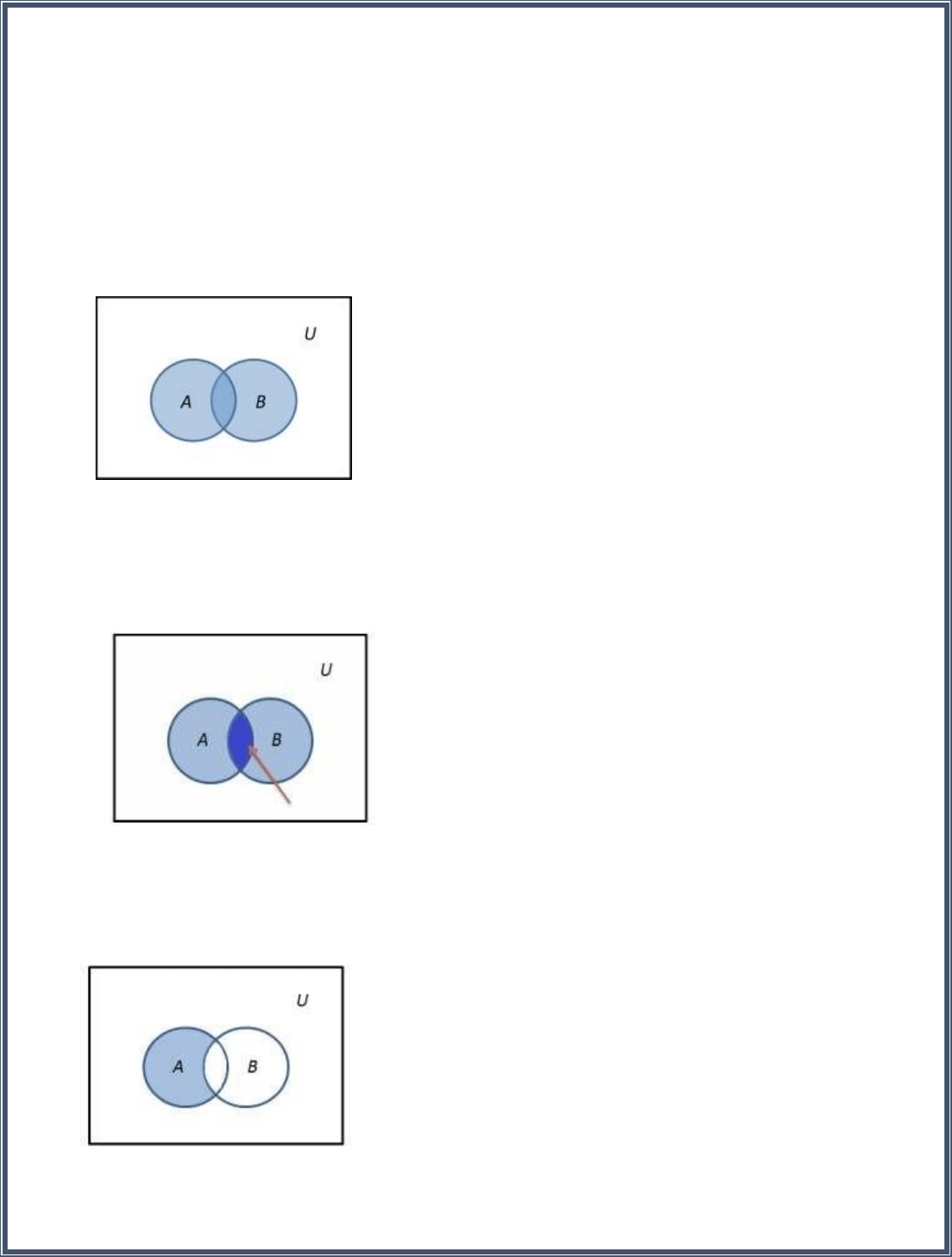
Unión
El conjunto de todos los elementos que pertenecen a A o a B, o tanto a A como a B, se
llama la unión de A y B y se escribe A 𝖴 B. (Área sombreada).
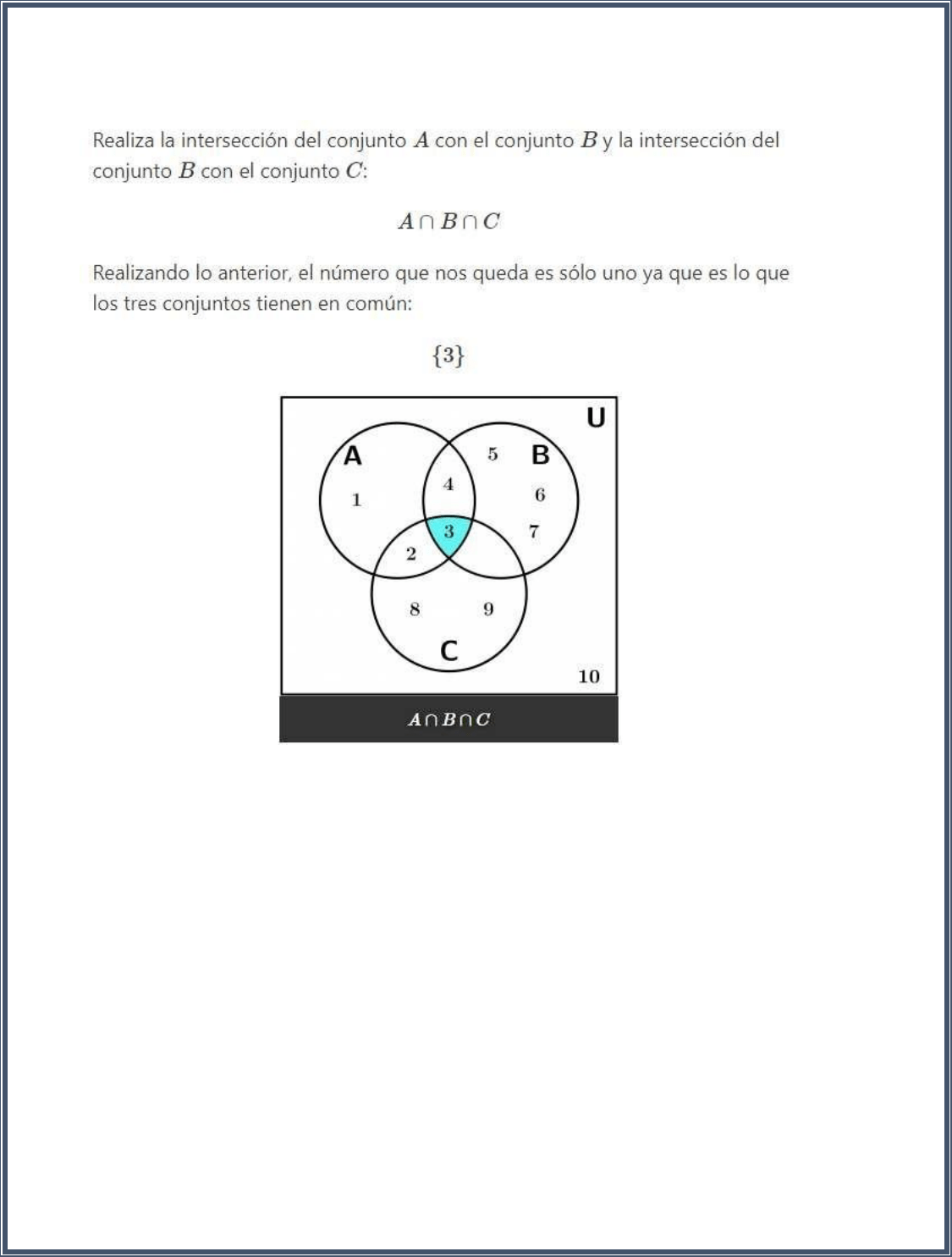
Intersección
El conjunto de todos los elementos que pertenecen simultáneamente a A y B se llama
la intersección de A y B y se escribe A ∩ B. (Área sombreada).
Diferencia
El conjunto que consiste en todos los elementos de A que no pertenecen a B se llama
la diferencia de A y B y se escribe A – B. (Área sombreada).
lOMoARcPSD|212725 42
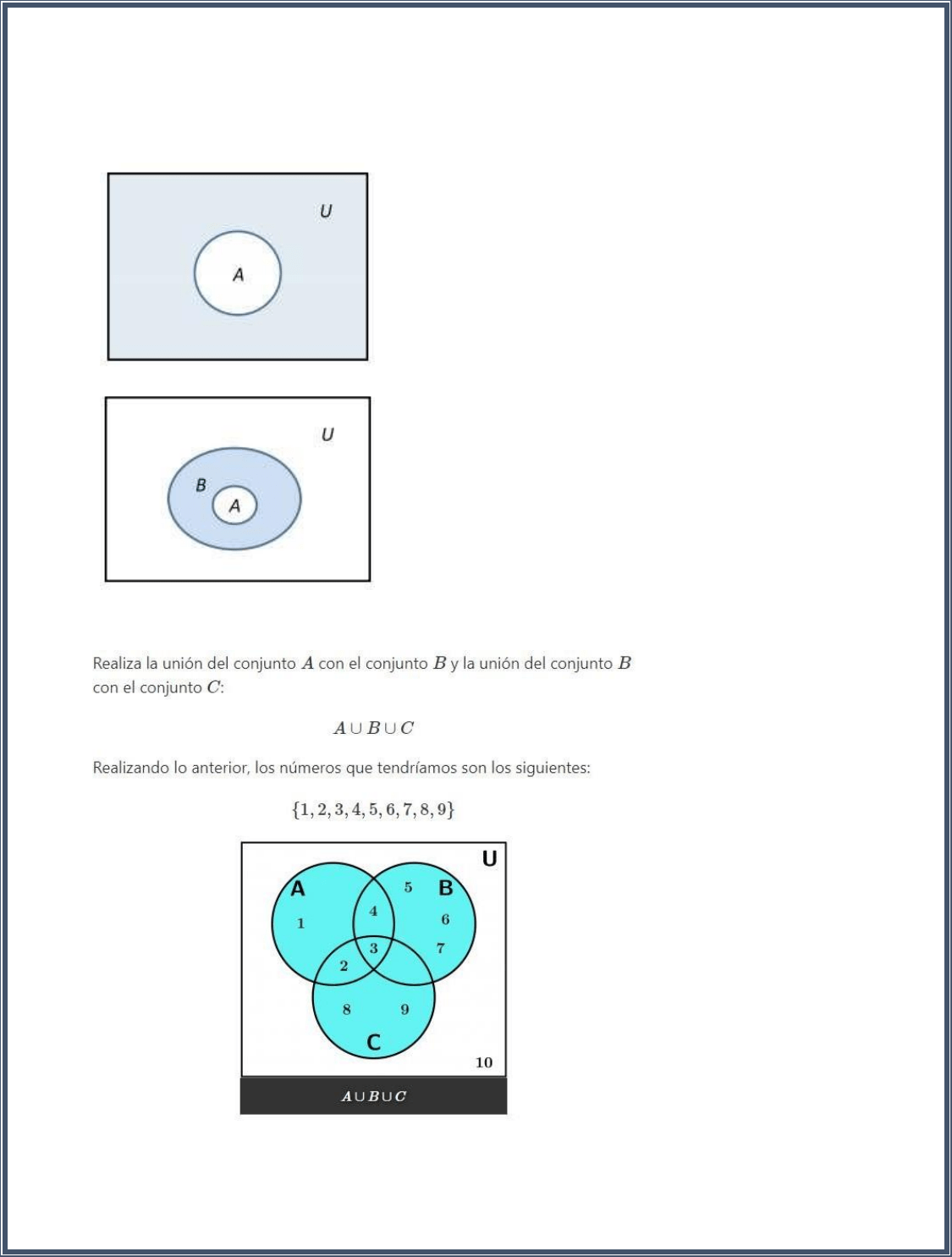
Complemento
Son todos los conjuntos no en A y se escribe A’. (Área sombreada).
Ejemplos:
lOMoARcPSD|212725 42
Conclusión
Este tema me pareció muy interesante y fácil de entender para mí ya que los conjuntos
sirven para agrupar objetos de la misma naturaleza para clasificarlos en “colecciones” o
“conjuntos” lo cual es parte de la vida diaria de todos los seres humanos
teoria-de-conjuntos (1)_organized.pdf
browser_emoji Estamos procesando este archivo...
browser_emoji Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
. . . . .