Departamento de Artes Plásticas
y Dibujo
DIBUJO TÉCNICO
BACHILLERATO
TEMA 4. TANGENCIAS
TEMA 4. TANGENCIAS.
Los OBJETIVOS generales que se pretende logren los alumnos al acabar el tema son:
Conocer las propiedades en las que se fundan los trazados de las tangencias, así como resolver y
construir adecuadamente los problemas básicos de tangencias, valorando el método de
razonamiento y su acabado y presentación. Cuestiones básicas son: saber poner y señalar
correctamente los puntos de tangencias y los centros de las circunferencias tangentes, así como
realizar correctamente los enlaces y las uniones.
CONCEPTOS Y PROCEDIMIENTOS.
1º BACHILLERATO
Tangencias
Metodología
Propiedades
Tangencia entre rectas y circunferencias
Tangencia entre circunferencias
Nociones y aplicación de la potencia y eje radical.
Casos especiales y aplicaciones en el dibujo técnico.
Enlaces
Propiedades
Construcción de enlaces.
2º BACHILLERATO
sPropiedades de las tangencias.
sEnlaces, planteamiento y aplicación.
sTrazado de circunferencias sin conocer el radio.
sEstudio sistemático de tangencias: circunferencias que pasan o son tangentes a...
sTres puntos.
sDos puntos y una recta.
sDos rectas y un punto.
sTres rectas.
sDos puntos y una circunferencia.
sUn punto, una recta y una circunferencia.
sDos rectas y una circunferencia.
sUna recta y dos circunferencias.
sUn punto y dos circunferencias.
sTres circunferencias.
TANGENCIAS
Nombre alumno Fecha
Nombre láminaN. lámina Nota:
Curso:
PROPIEDADES DE LAS TANGENCIAS:
1. Si dos circunferencias son tangentes entre sí, el punto de tangencia
se encuentra en la recta que une los centros. (figura 1)
T
O1
O2
CIRCUNFERENCIAS
TANGENTES EXTERIORES
Cuando queramos dibujar una circunferencia que sea tangente a otra
circunferencia y que además pase por un punto de tangencia de esta última,
lo que tenemos que hacer es unir el centro de la circunferencia con el punto
de tangencia y prolongar.
En esta recta estarán todos los centros de las circunferencias (infinitas) que
son tangentes a la primera.
T
O1
2. Si una recta es tangente a una circunferencia, el radio en el punto de
tangencia es perpendicular a la tangente.
Cuando queramos hallar una circunferencia que sea tangente a una recta por
un punto de tangencia de ésta lo primero que tenemos que hacer es levantar
una perpendicular por este punto a la recta.
T
O1
r
90º
T
t
t
3. Recordemos que una mediatriz es la recta de todos los puntos que equidistan
de otros dos (extremos de un segmento). Por lo tanto el centro de cualquier
circunferencia que pase por dos punto está en la mediatriz del segmento que lo
forman.
figura 1
figura 5
figura 2
figura 3
figura 3
figura 4
figura 4
T
O1
O2
CIRCUNFERENCIAS
TANGENTES INTERIORES
Se pueden hacer exteriores o interiores.
T
P
Mediatriz PT
figura 5
figura 2
4. El centro de cualquier circunferencia tangente
a dos rectas se encuentra en la bisectriz del ángulo
que lo forman.
T
O1
r
t
figura 6
figura 6
T
P
O1
Aplicación de los principios anteriores en un caso de tangencias:
T
P
O1
Primer paso
Segundo paso
Mediatriz PT
- Circunferencia tangente a una circunferencia que pase por un punto T de
tangencia de ésta y pon un punto P exterior.
figura 7
figura 7
1. Se aplica la propiedad 1: se une el centro O1 con el punto de tangencia T
2. Se une P con T y se halla la mediatriz de PT. Donde corte la mediatriz
con la primera recta estará el centro de la circunferencia buscada.
ENLACES: Es la unión de varias curvas tangentes entre sí o bien curvas con
rectas, creando un enlace continuo o curva continua.
O1
O2
O3
O1
r
T
T
O1O2 = r1+r2
O1O2 = r1-r2
Posiciones relativas de recta y circunferencia.
O1
r
t
Exteriores
T
O1
r
t
Tangentes
O1
r
t
Secantes
A
B
figura 7
Posiciones relativas de dos circunferencias.
O1
O2
Exteriores
r
1
r2
O1
r
1
O2
r2
Secantes
O1
r
1
O2
r2
Interiores
r
1
O
r2
Interiores
Posición relativa rectas y circunferencias.
Nombre alumno
TANGENCIAS
Fecha
Nombre láminaN. lámina
Curso:
Nota:
TANGENCIAS: Dos o más figuras geométricas son tangentes cuando únicamente tienen UN PUNTO EN COMÚN.
Los casos que nosotros vamos a estudiar son entre circunferencias o entre circunferencias y rectas.
La construcción de tangencias sirve, básicamente, para diseñar objetos, figuras o planos donde intervengan curvas
realizadas con compás.
joyas
instrumental
arquitectura
muebles
Poleas
juguetes
juegos
grifos
encadenados
objetos industriales
ganchos
1.- Dibujar 2 circunferencias radio 10 mm. que sean
TANGENTES EXTERIORES a la dada y entre ellas.
3.- Dibujar las circunferencias de r = 12 mm.,
TANGENTES a la dada y que pase por el PUNTO P.
P
O1
4.- Circunferencias tangentes a otra de r = 18 mm. dada,
que pase por un punto P exterior y por un punto de
tangencia T.
T
5.- Hallar las circunferencias tangentes
COMUNES EXTERIORES de r= 12 mm., a las
circunferencias dadas O1 y O2.
O1
P
O1
O1
6.- Hallar las circunferencias tangentes
COMUNES INTERIORES de r= 35 mm.,
a las circunferencias dadas O1 y O2.
Nombre alumno
TANGENCIAS ENTRE CIRCUNFERENCIAS
Fecha
Nombre láminaN. lámina
Curso:
Nota:
O1
O1
R = 23 mm
2.- Dibujar 2 circunferencias radio 10 mm. que sean
TANGENTES INTERIORES a la dada y entre ellas.
R = 32 mm
R = 18 mm
El radio de la circunferencia que se busca se sabrá cuando se acabe
el ejercicio.
O1= 10 mm
O2 = 15 mm
O1-O2 = 40 mm
O2
O1= 10 mm
O1-O2 = 30 mm
O2 = 15 mm
O2
1.- Dibujar 2 circunferencias radio 10 mm. que sean
TANGENTES EXTERIORES a la dada y entre ellas.
3.- Dibujar las circunferencias de r = 12 mm.,
TANGENTES a la dada y que pase por el PUNTO P.
P
O1
4.- Circunferencias tangentes a otra de r = 18 mm. dada,
que pase por un punto P exterior y por un punto de
tangencia T.
T
5.- Hallar las circunferencias tangentes
COMUNES EXTERIORES de r= 12 mm., a las
circunferencias dadas O1 y O2.
O1
P
O1
O1
6.- Hallar las circunferencias tangentes
COMUNES INTERIORES de r= 35 mm.,
a las circunferencias dadas O1 y O2.
Nombre alumno
TANGENCIAS ENTRE CIRCUNFERENCIAS
Fecha
Nombre láminaN. lámina
Curso:
Nota:
T1
T2
O1
O2
O3
T1
T2
O1
O2
O3
R = 23 mm
R = 10 mm
2.- Dibujar 2 circunferencias radio 10 mm. que sean
TANGENTES INTERIORES a la dada y entre ellas.
R = 32 mm
R = 10 mm
R = 18 mm
T1
T2
O2
O3
El radio de la circunferencia que se busca se sabrá cuando se acabe
el ejercicio.
O1= 10 mm
O2 = 15 mm
O1-O2 = 40 mm
O3
O2
O4
O1= 10 mm
O1-O2 = 30 mm
O2 = 15 mm
O2
O3
O4
1.-Dibuja la recta r tangente a la circunferencia O1
por el punto dado de tangencia (T).
2.- Dibuja la circunferencia de radio 13 mm. que
sea tangente a la recta dada y que pase por el
punto T dado.
3.- Dibuja las rectas tangentes a la circunferencia 01
dada y que pasen por P
P
O1
4.- Dibuja la circunferencia de radio 15 mm. que
sea tangente a las rectas que se cortan dadas.
5.- Hallar las RECTAS tangentes COMUNES
EXTERIORES a las dos circunferencias dadas..
O1
O1
O2
TANGENCIAS ENTRE RECTAS Y CIRCUNFERENCIAS
Nombre alumno
T
O1
T
6.- Hallar las RECTAS tangentes COMUNES
INTERIORES a las dos circunferencias dadas..
Fecha
Nombre láminaN. lámina Nota:
Curso:
O2
O1= 14 mm
O2 = 23 mm
O1= 10 mm
O2 = 22 mm
1.-Dibuja la recta r tangente a la circunferencia O1
por el punto dado de tangencia (T).
2.- Dibuja la circunferencia de radio 13 mm. que
sea tangente a la recta dada y que pase por el
punto T dado.
3.- Dibuja las rectas tangentes a la circunferencia 01
dada y que pasen por P
P
O1
4.- Dibuja la circunferencia de radio 15 mm. que
sea tangente a las rectas que se cortan dadas.
5.- Hallar las RECTAS tangentes COMUNES
EXTERIORES a las dos circunferencias dadas..
O1
O1
O2
TANGENCIAS ENTRE RECTAS Y CIRCUNFERENCIAS
Nombre alumno
T
O1
T
6.- Hallar las RECTAS tangentes COMUNES
INTERIORES a las dos circunferencias dadas..
Fecha
Nombre láminaN. lámina Nota:
Curso:
O1
O1
15 mm
15 mm
O2
T1
T2
T3
T4
T1
T2
T3
T4
O1= 14 mm
O2 = 23 mm
O1= 10 mm
O2 = 22 mm
1.-Dibujar una circunferencia tangente a la recta r y que
pase por el punto P. (Circunferencia que pasa por 2
puntos)
TANGENCIAS III
Nombre alumno
T
Fecha
Nombre láminaN. lámina Nota:
Curso:
P
2.- Circunferencias tangentes a una recta r dada, que
pasan por un punto P y que tiene de radio 20 mm.
P
4.- Dibujar las circunferencias tangentes a dos rectas
r y s dado el punto de tangencia T en una de ellas.
T
3.- Hallar las circunferencias tangentes a una recta r
y que pasan por dos puntos dados A y B. (aplicación de
eje radical)
A
B
r
5.- Dibujar las circunferencias tangentes a O1 por el
punto de tangencia dado T y a la recta r.
6.- Representar las circunferencias de radio 20 mm.
tangentes comunes a la circunferencia y a la recta dadas.
r
r
r
t
T
r
o
r
o
1.-Dibujar una circunferencia tangente a la recta r y que
pase por el punto P. (Circunferencia que pasa por 2
puntos)
Nombre alumno
T
Fecha
Nombre láminaN. lámina Nota:
Curso:
P
2.- Circunferencias tangentes a una recta r dada, que
pasan por un punto P y que tiene de radio 20 mm.
P
4.- Dibujar las circunferencias tangentes a dos rectas
r y s dado el punto de tangencia T en una de ellas.
T
T2
T1
3.- Hallar las circunferencias tangentes a una recta r
y que pasan por dos puntos dados A y B. (aplicación de
eje radical)
A
B
T
T
r
5.- Dibujar las circunferencias tangentes a O1 por el
punto de tangencia dado T y a la recta r.
r
r
r
t
T
r
6.- Representar las circunferencias de radio 20 mm.
tangentes comunes a la circunferencia y a la recta dadas.
r= 20
h=20
o1
o2
o1
o1
o2
o1
o2
o1
o2
o
o
o1
o2
Habrían dos resultados más al otro extremo de la
circunferencia O
r
TANGENCIAS III
1.- Trazar tres circunferencias tangentes entre sí, dados
sus respectivos radios.
Nombre alumno Fecha
Nombre láminaN. lámina Nota:
Curso:
TANGENCIAS IV
r1
r2
r3
2.- Trazar tres circunferencias tangentes entre sí,
conocidos sus centros respectivos.
o1
o2
o3
3.- Dibujar las circunferencias de igual radio y tangentes
interiores a los lados de los ángulos de los vértices del
pentágono.
3.- Dibujar las circunferencias de igual radio y tangentes
interiores a los lados de los ángulos de los vértices del
pentágono.
5.- Dadas las tres rectas r, s y t que se cortan entre sí,
trazar una circunferencia tangente común a las tres.
6.- Dibuja la circunferencia que es tangente a la recta r,
pasa por el punto P que está en la recta t y además
tiene el centro en t.
P
r
t
o3
r
t
s
1.- Trazar tres circunferencias tangentes entre sí, dados
sus respectivos radios.
Nombre alumno Fecha
Nombre láminaN. lámina Nota:
Curso:
o1
TANGENCIAS IV
o2
o3
r1
r2
r3
r2
r1
r1
r3
r3
r2
T
T
T
2.- Trazar tres circunferencias tangentes entre sí,
conocidos sus centros respectivos.
o1
o2
o3
T
T
T
3.- Dibujar las circunferencias de igual radio y tangentes
interiores a los lados de los ángulos de los vértices del
pentágono.
o´
o
3.- Dibujar las circunferencias de igual radio y tangentes
interiores a los lados de los ángulos de los vértices del
pentágono.
o´
5.- Dadas las tres rectas r, s y t que se cortan entre sí,
trazar una circunferencia tangente común a las tres.
o
T
T
T
6.- Dibuja la circunferencia que es tangente a la recta r,
pasa por el punto P que está en la recta t y además
tiene el centro en t.
P
o
T
r
t
o3
r
t
s
1.- Dibujar la circunferencia tangente a dos circunferencias O1 y O2, dado el punto de tangencia de una de ellas.
Nombre alumno Fecha
Nombre láminaN. lámina Nota:
Curso:
O1
O2
T
TANGENCIAS V
2.- Dadas las rectas r y t y el punto P, dibujar las circunferencias tangentes a las rectas r y t y que pasen por P.
P
r
s
1.- Dibujar la circunferencia tangente a dos circunferencias O1 y O2, dado el punto de tangencia de una de ellas.
Nombre alumno Fecha
Nombre láminaN. lámina Nota:
Curso:
TANGENCIAS V
O1
O2
O3
O4
O5
O6
T
T
T
2.- Dadas las rectas r y t y el punto P, dibujar las circunferencias tangentes a las rectas r y t y que pasen por P.
P
r
s
P
O1
T1
T2
O2
O3
T3
T4
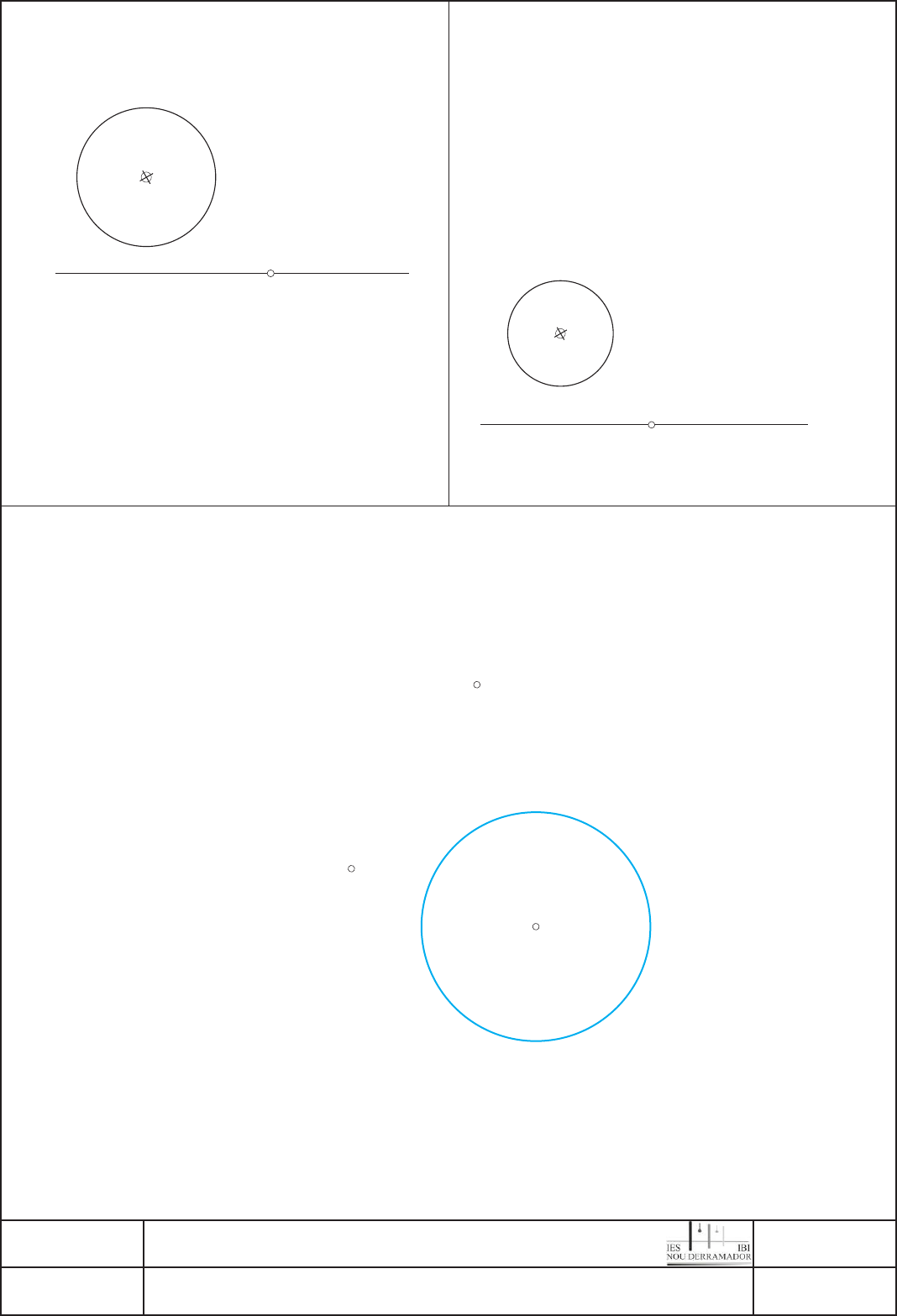
1.- Dibuja la circunferencia tangente exterior a O1 y a
la recta r por el punto de tangencia T.
Nombre alumno Fecha
Nombre láminaN. lámina Nota:
Curso:
TANGENCIAS VI
O1
T
1.- Dibuja la circunferencia tangente interior a O1 y a la
recta r por el punto de tangencia T.
O1
T
r
r
N
M
O
1.- Dibuja las circunferencias tangentes a la circunferencia dada O y que pase por los puntos M y N
Este documento contiene más páginas...
Descargar Completo
TEMA 4 TANGENCIAS.pdf
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.