
FINAL MATEMATICA BLUMENFARB 2015 EQUIPO MENSAJERO PARA
TEMA 1 GEOMETRIA
1) Dar ecuación de una hipérbola con eje de simetría en y; cuál es la
relación entre a, b y c; definir como conjunto de puntos y como intersección
de superficies, graficar y nombrar un ejemplo aplicado a la arquitectura.
La hipérbola es el lugar geométrico de los puntos en donde la diferencia de
sus distancias a dos puntos fijos, los focos, es siempre constante. Si se corta
con un plano a una superficie cónica en ángulo paralelo al eje se obtiene una
hipérbola. Estructuras de soporte como columnas y torres. Columnas
Oscar Niemayer. Catedral de Brasilia.
2) Elipse, dar su ecuación que tenga su vértice en el origen de coordenadas
y cuando se apoye sobre el eje y (es vertical), nombrar la relación de sus
paramitos a, b y c y dar algún ejemplo en diseño.
La elipse es el lugar geométrico de todos los puntos de un plano tales que la
suma de las distancias a otros dos puntos fijos, los focos, es constante. La
elipse se da cuando se intersecta con un plano en ángulo distinta a la
generatriz en una superficie cónica de revolución. Entre a, b y c existe la
relación pitagórica ya que se puede armar un triángulo rectángulo entre ellas.

El a es el semi eje mayor, b es el semi eje menor y c la distancia entre el
centro y el foco. La excentricidad caracteriza la forma del elipse.
Cuanto más próximo a cero sea el valor de la excentricidad más redondeada.
Se define Teatro Nacional De Beijing y Torre García de Almería.
3) Defina parábola como conjunto de puntos y como intersección entre
planos. Ecuación cuando no está en el eje de coordenadas. Ej. numérico de
éste. Ej. puntual de una obra de arquitectura que use parábolas.
Se denomina parábola al lugar geométrico de los puntos de un plano que
equidistan de una recta dada, la directriz, y de un punto exterior a ella, el

foco. La parábola se obtiene como intersección de planos al cortar una
superficie cónica en ángulo igual al de la generatriz.
El Colegio de Santa Teresa, el Palacio Güell, la Casa Batlló y la casa Milà.
4) Superficies cónicas, cono circular recto, ecuación, qué curvas se generan
con la superposición de planos.
Una superficie cónica es una superficie reglada, puede ser de revolución o
de no revolución. Se trata de una recta, la generatriz, la cual se apoya en una
curva, la directriz, y pasa por un punto, el vértice, el cual está no está en el
mismo plano que la directriz. Una superficie cónica de revolución es
engendrada cuando la generatriz rota alrededor de una recta fija, el eje. La
generatriz corta al eje en un punto, el vértice. Es un cono circular recto si la
directriz es una circunferencia. Las curvas que salen de un cono circular recto
son: Al cortar el cono en un ángulo paralelo al eje se obtiene una hipérbola,
en un ángulo paralelo a la generatriz, una parábola. Si corta en ángulo
diferente a la generatriz se da un elipse, y si se corta en el plano con ángulo
igual a 0° se da una circunferencia.

5) Superficies cilíndricas. 3 ejemplos distintos, fórmulas y dibujos.
Una superficie cilíndrica es generada por una recta que se desplaza
paralelamente a si misma apoyada en una curva directriz. Una ecuación que
contenga dos variables, si representa una curva en el plano de dichas
variables, será la ecuación de una superficie cilíndrica recta cuyas
generatrices son paralelas a la variable faltante.

6) Indicar qué paraboloides conoce. Trazas. Ejemplo numérico. Ejemplos de
diseño. Son superficies regladas? Pueden ser engendradas por revolución?
El paraboloide hiperbólico es una superficie doblemente reglada ya que
admite dos familias uniparamétricas de rectas. Ópera de Sídney

7) Qué tipos de hiperboloides conoce? Dar formula, decir por que son
superficies regladas y cuando son de revolución. Dar ejemplos en
arquitectura.
Se llama superficies regladas a las engendradas por rectas paralelas a una
dirección dada variable, que se desplazan por una curva llamada directriz.
Hay distintos tipos de superficies regladas. Las superficies cilíndricas son
generadas por rectas paralelas a si misma apoyadas en una curva, directriz,
las rectas que generan las superficies se llaman generatrices. Es una
superficie cilíndrica si las generatrices son perpendiculares al plano que
contiene la directriz. Una ecuación que contenga dos variables si representa
una curva en el plano de dichas variables, será la ecuación de una superficie
cilíndrica recta, cuyas generatrices son paralelas al eje de la variable faltante
o ausente. Además están las superficies cónicas, las cuales son generadas
cuando la generatriz se desplaza por la curva directriz pero atraviesa un
vértice no perteneciente al plano de la curva.
Se dice que una superficie es de revolución si está engendrada por la
rotación de una curva, la generatriz, alrededor de una recta fija, el eje,
contenida en el plano de la curva.
Ej. 1. Cono Circular recto. Puede ser una superficie reglada, como directriz se
utilizaría una circunferencia y las reglas deberían pasar por un vértice. El
cono es una cuádrica degenerada. Ej. 2. Paraboloide elíptico
Si además es a = b, el paraboloide elíptico será un paraboloide de
revolución, que es la superficie resultante de girar una parábola en torno a
su eje de simetría. Las antenas parabólicas son paraboloides de revolución, y
tienen la propiedad de reflejar los rayos paralelos entrantes hacia su foco,
punto donde se ubica el receptor. (No puede ser superficie reglada ya que no
podría proyectarse un paraboloide elíptico a través de una directriz y
generatriz). Catedral de Brasília. Oceanogràfic de Valencia

El hiperboloide de una hoja es una superficie doblemente reglada
en el sentido de que admite dos familias uniparamétricas de rectas.
8) Definir superficies regladas, cuáles son y dar dos ejemplos numéricos y
graficar. Ej. de arquitectura de ellos.
Se llama superficies regladas a las engendradas por rectas, generatrices,
paralelas a una dirección dada variable, que se desplazan por una curva
llamada directriz. Hay dos tipos de superficies regladas, las cilíndricas y las
cónicas. En las superficies cilíndricas las generatrices son paralelas entre sí,
y en las cónicas las generatrices se apoyan en la directriz y pasan todas por
un punto fijo, el vértice. Si las generatrices son perpendiculares al plano de la
directriz, son superficies cilíndricas rectas. Una ecuación que contenga dos
variables, si representa a una curva en el plano de dichas variables, esta será
la ecuación para una superficie cilíndrica recta cuyas generatrices son
paralelas al eje de la variable faltante o ausente.
Ej. Cilíndrico elíptico y cilindro hiperbólico. Oceanogràfic de Valencia

TEMA 2 GRAFOS
9) Definir mosaico, explicar matemáticamente, realizar un mosaico por
adición y sustracción y colorearlo explicando la teoría de coloración de
grafos.
Mosaico es todo recubrimiento del plano generado mediante polígonos que
no permiten agujeros ni solapamientos. Si los polígonos son regulares el
mosaico es regular. Para ello se deben usar triángulos equiláteros, cuadrados
o hexágonos. El problema de coloración nace cuando se intenta resolver la
duda de cuantos colores son requeridos para colorear un mapa sin que haya
países aledaños de un mismo color. Se requieren cuatro colores para
colorear cualquier mapa poligonal. (si es plano y conexo) Si los vértices son
de grado par con dos colores alcanza, si son de grado impar es
imprescindible usar al menos tres colores.
10) Qué es un grafo regular? Recorrido euleriano, clasificación según sus
vértices (explique cuándo es restringido y cuándo no), dar un ejemplo de
cada uno.
Un grafo es regular cuando posee al
menos tres caras y los grados de sus
vértices son iguales entre si. Y es
completamente regular cuando,
además, todas sus caras tienen igual
número de aristas que las rodean.
El recorrido euleriano se da cuando
se puede recorrer un grafo conexo
pasando una sola vez por cada
arista. Si el ciclo comienza y termina
en el mismo vértice es general, si no
es restringido.
11) Cuáles son los polígonos que permiten el recubrimiento total del plano?
Cómo se verifica esto?
Podría recubrirse el plano con los siguientes polígonos regulares:
Triángulo equilátero, cuadrados, y hexágonos.

Partiendo de la premisa de:
Siendo n el número de aristas y
suponiendo que el polígono en
cuestión es regular planteamos:
En el triangulo n=3. Entonces sus
ángulos interiores serán de 60º.
En el cuadrado n=4, sus ángulos
interiores son de 90º. En el hexágono
n=6, sus ángulos interiores de 120º.
Entonces: Se precisaran como mínimo tres polígonos regulares ya que la
suma de sus ángulos interiores debe ser igual a 360º porque de no ser así no
estarían en un plano. Como podemos apreciar eso se logra en los triángulos,
cuadrados y hexágonos solamente ya que la amplitud de cada ángulo interior
es divisor de 360º.
12) Sección áurea. Crear el rectángulo áureo. Ej. de la arquitectura.
El numero de oro y la proporción aurea surge de la sucesión de Fibonacci, la
división entre dos términos consecutivos, el mayor sobre el menor, obtiene un
número que mientras más grandes sean los términos más se acerca a φ,
(1,6803).
El alzado del Partenón griego de Atenas, la pirámide de Keops (el consciente
entre la altura de uno de los triángulos que forma la pirámide y el lado es dos
φ).

13) Definir grafo plano, Cuándo es regular y cuándo completamente regular?
Recorrido euleriano, formula de Euler, y grafo dual.
Un grafo es grafo plano si, y sólo si
es isomorfo a un grafo que puede
dibujarse en el plano de forma tal
que las aristas sólo se toquen en los
vértices. Un grafo es regular cuando
posee al menos tres caras y los
grados de sus vértices son iguales
entre si. Y es completamente
regular cuando, además, todas sus
caras tienen igual número de aristas
que las rodean.
El recorrido euleriano se da cuando
se puede recorrer un grafo conexo
pasando una sola vez por cada
arista. Si el ciclo comienza y termina
en el mismo vértice es general, si no
es restringido. C+V=A+2 (contando
cara del infinito). Se denomina grafo dual, cuando a un grafo plano se le
asigna a cada cara (incluyendo la del infinito) un vértice y se los une pasando
una arista del grafo dual por cada una del grafo asociado.
13) Número de oro, definición. Cómo se procede para dividir un segmento
en media y extrema razón? Mostrarlo gráficamente. Cómo se construye un
rectángulo áureo a partir de un cuadrado de 5 cm de lado? Asignar un valor
arbitrario al lado del mismo y calcular su área. Mencionar alguna aplicación
arquitectónica de dicho número.
El numero de oro y la proporción aurea surge de la sucesión de Fibonacci, la
división entre dos términos consecutivos, el mayor sobre el menor, obtiene un
número que mientras más grandes sean los términos más se acerca a φ,
(1,6803). El alzado del Partenón griego de Atenas, la pirámide de Keops (el
consciente entre la altura de uno de los triángulos que forma la pirámide y el
lado es dos φ).
1) Se traza el punto medio m del
segmento AB, y por el punto B se
traza una perpendicular logrando el
punto D, de forma tal que BD sea
igual a AB/2.
2) Se traza el segmento AD.
3) Se transporta sobre AD el
segmento BD obteniendo el punto E
tal que BD sea igual a DE.
4) Abatiendo el punto E sobre el
segmento AB se obtiene el punto C.

14) Definir grafo poligonal. Cuándo es regular? Cuándo es completamente
regular? Mencionar todos los grafos poligonales y dibujar dos. Todos los
grafos cumplen con la ley de Euler o hay excepciones?
Para definir grafo poligonal, primero definamos grafo plano. Un grafo plano
es plano si, y sólo si, es isomorfo a un grafo que puede dibujarse en el plano
de forma tal que las aristas sólo se toquen en los vértices. Los grafos no
planos son dos: el K3,3 y el K5. Cualquier grafo isomorfo de estos, o que
tenga un subgrafo que sea alguno de estos dos no es plano. Entonces, un
grafo poligonal es un grafo plano conexo el cual es una reunión de ciclos tal
que existe un ciclo mínimo y uno máximo. Un grafo poligonal divide el plano
en zonas poligonales. El interior de cada ciclo se conoce como cara.
Puede comprobarse que el número de caras más el número de vértices es
igual al numero de aristas más dos. Esto se conoce también como la ley de
Euler. C + V = A + 2. Todos los poliedros regulares pueden expresarse como
grafos poligonales. Estos son: El tetraedro, el cubo (hectaedro), el octaedro,
el dodecaedro y el icosaedro. Un grafo poligonal es regular cuando el grado
de cada vértice es igual. Un grafo poligonal es completamente regular si
cada cara limita con la misma cantidad de aristas.

15) Defina grafos poligonales, construya un grafo de 4 caras y 6 vértices.
¿Cuales son los poliedros regulares, nómbrelos todos y dibuje como mínimo
tres y por que polígonos están regidos.
Un Grafo poligonal es un grafo
simple, plano conexo, que resulta de
unir dos o más ciclos; así, hay un
ciclo mínimo y uno máximo; en
donde la suma de las caras más la
suma de los vértices es igual a la
suma de las aristas más dos. Los
poliedros regulares son el tetraedro,
el cubo, el octaedro, el dodecaedro
y el icosaedro.
16) Definir grafo plano, dar condición necesaria y suficiente para que sea
plano, definir recorrido euleriano, explicar los tipos de recorridos eulerianos.
Un grafo plano es un grafo conexo en donde el único contacto entre aristas
se da en los vértices. Para que un grafo sea plano no puede tener ningún
subgrafo que sea K3,3 o K5.
Recorrido Euleriano: que comienza y termina
en un mismo vértice pasando exactamente una vez sola por arista. Para que
esto exista el grafo debe ser conexo y el grado de todos los vértices par.
Ciclo Hamiltoniano, es un recorrido similar. Es un ciclo que comienza y
termina en un mismo vértice pasando exactamente una vez por cada vértice.

TEMA 3 DERIVADAS E INTEGRALES
17) Aplicaciones geométricas de las integrales; dar un ejemplo numérico y
graficar.
Las aplicaciones geométricas de una integral definida son área, volumen y
longitud de una curva. Para calcular el área entre una curva y el eje x se
utiliza un integral definido.
Se utiliza también para medir longitud de una curva con la siguiente formula:
Finalmente para el volumen también se puede utilizar integrales. Sobre todo
para cuerpos engendrados por la revolución de una curva. Dada la formula
f(x) para calcular el volumen de revolución a través del eje x se utiliza:
Ej. de área entre la curva y los ejes
coordenados.

18) Derivada aplicación geométrica. Máximos y mínimos, explicar el
criterio para que sea suficiente, ejemplo numérico sencillo.
Los máximos y mínimos son puntos críticos (el punto de la curva en el cual la
pendiente de la recta tangente es igual a 0).
La condición necesaria para que exista un máximo, si existe f ´ (x) y f ´´ (x),
es que f ´ (x) = 0 y f ´´ (x) < 0.
La condición necesaria para que exista un mínimo, si existe f ´ (x) y f ´´ (x),
es que f ´ (x) = 0 y f ´´ (x) > 0.
Ej.: f(x) = x3 - 3x2 + 1 = 0
La derivada es f ´ (x) = 3x2 - 6x = 0 (La primera condición ya está para
ambos)
Resolviendo la derivada nos da x = 2, x = 0
La segunda derivada es f ´´ (x) = 6x - 6
Para 0 ---- > 6(0) - 6 = -6
-6 < 0 ---- > se trata de un máximo... en el punto de la curva donde x = 0 hay
un punto máximo.
Para 2 ---- > 6(2) - 6 = 6
6 > 0 ---- > se trata de un mínimo.... en el punto de la curva donde x = 2 hay
un punto mínimo
19) Mencione momento de 1º orden, de 2º orden y baricentro de: un
sistema de puntos sobre una recta, en el plano, placas planas y superficies
de revolución; Trabajo; Obtener la ecuación horaria y la de la velocidad de un
objeto en movimiento a partir de la ecuación de la aceleración.
Llamamos momento 1º orden o momento estático a la suma de productos
de cada uno de los valores de masa y sus respectivos valores de abscisas.
De la misma manera podemos definir el momento de 2º orden o momento
de inercia: será la suma de los productos entre cada uno de los valores de
masa y sus respectivos valores de abscisas elevados al cuadrado.
El centro de gravedad o baricentro es el punto donde al calcular el
momento estático respecto de él el resultado será 0. En un conjunto de
masas alineadas donde el momento estático es no nulo.
Tenemos tres masas puntuales M1=5gr M2=3gr y M3=2gr Se encuentran
ubicadas respectivamente en los puntos cuyas abscisas son x1=4cm, X2=-
2cm y X3=-3cm. Ahora hallaremos el baricentro del sistema.
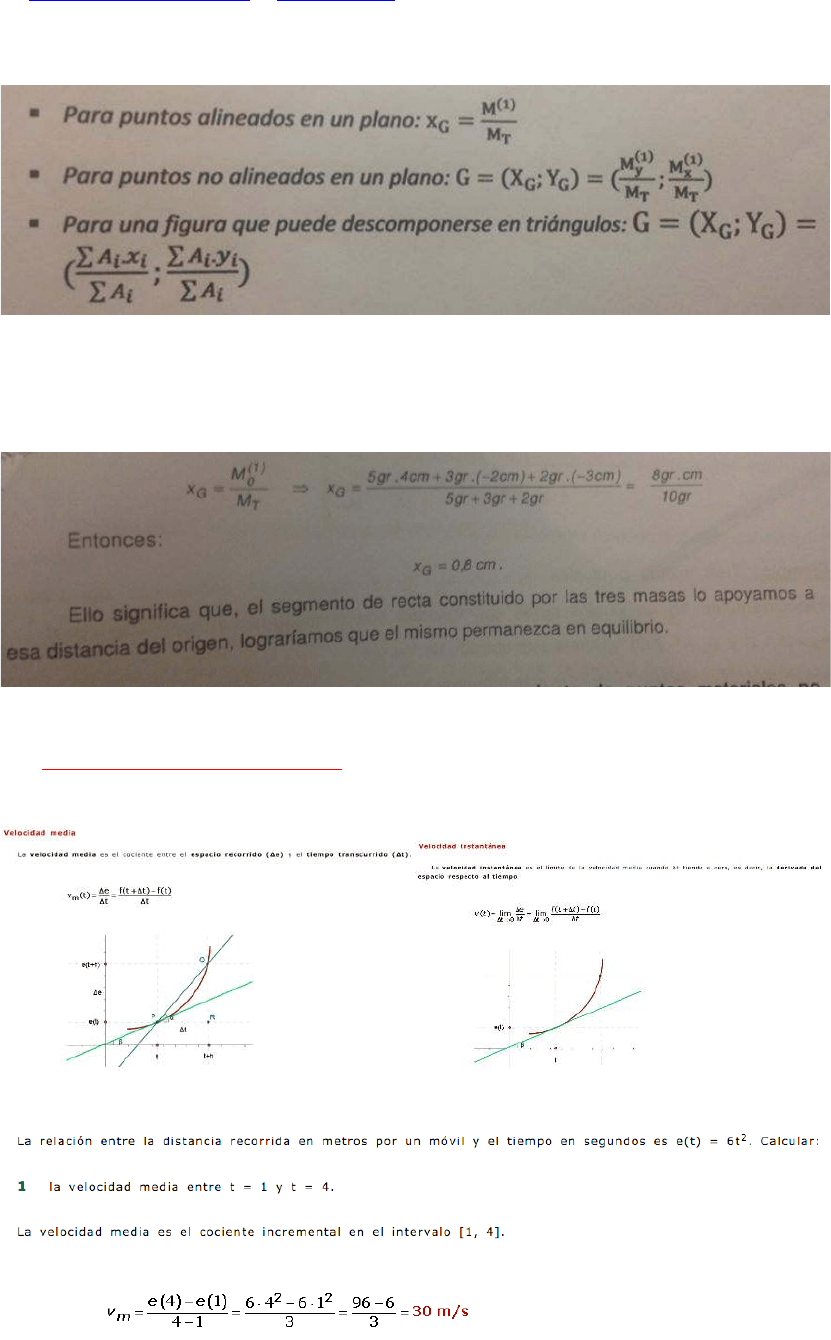
20) Derivada aplicación física. Ejemplo con el tiempo. (deslazamiento,
velocidad y aceleración).
Este documento contiene más páginas...
Descargar Completo
Resumen muy piola.pdf
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.