Ing. Juan Lancioni Física I – UTN – FRC
1
FISICA I UTN-FRC
UNIDAD 02: OPTICA GEOMÉTRICA
PROPAGACIÓN DE LA LUZ – LEYES DE REFLEXIÓN Y
REFRACCIÓN– REFLEXIÓN INTERNA TOTAL
(PRIMERA PARTE)
Introducción:
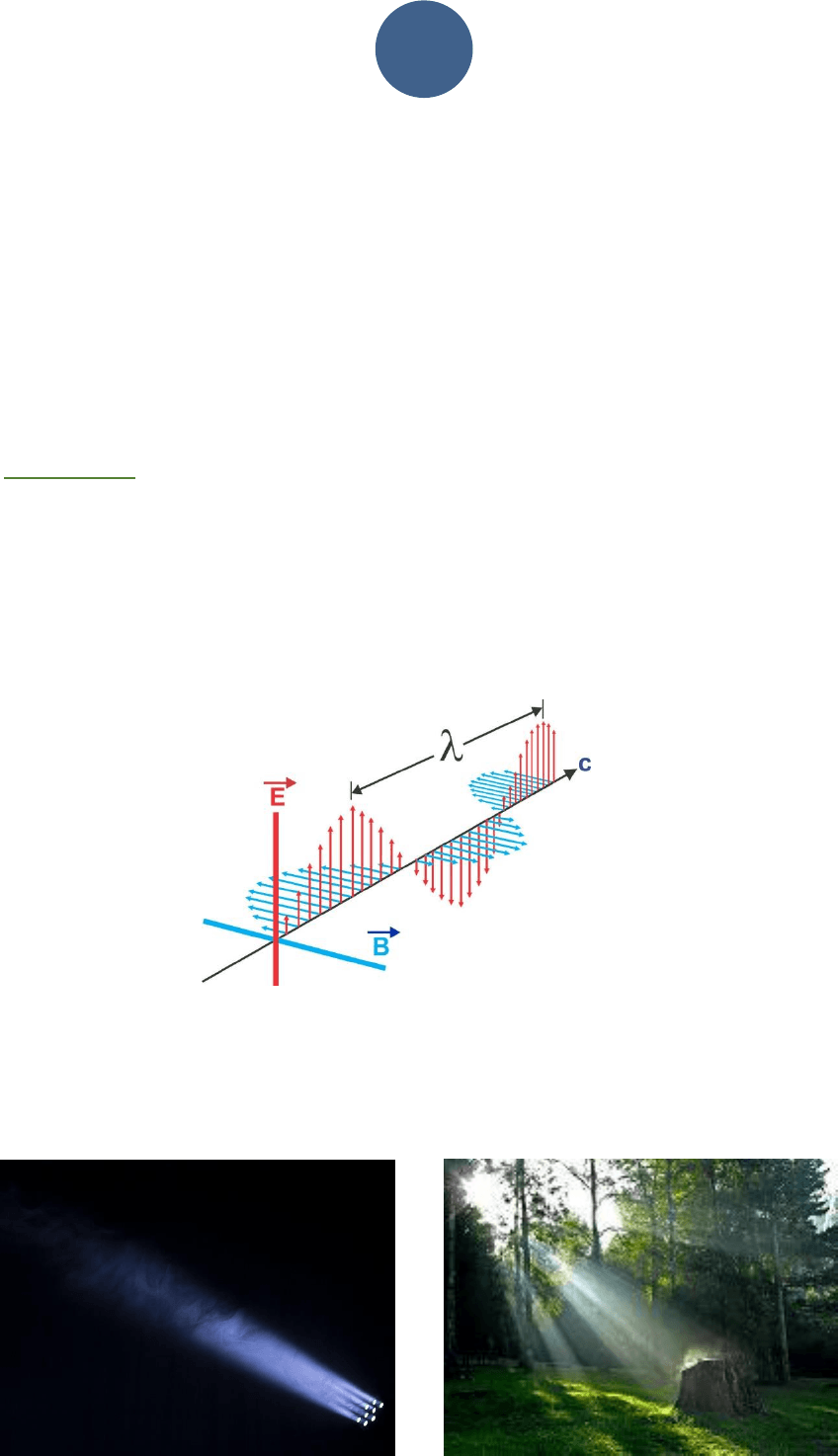
Sabemos que la luz es, a la vez onda y partícula. De ahí que la descripción del fenómeno
luz puede ser considerado como Ondulatorio o Corpuscular, según sea la circunstancia.
Lo más exacto para el caso de la Óptica Geométrica es considerar a la luz como una onda
electromagnética, cuya rapidez y otras propiedades se pueden derivar de las ecuaciones
de Maxwell.
Ocurre que en muchas circunstancias las ondas viajan en línea recta, es decir, que son
líneas perpendiculares a los frentes de onda y se llaman rayos de luz. Por ejemplo: los
rayos de un proyector en una habitación con humo, el ingreso de un haz solar en un
paisaje, etc.
Ing. Juan Lancioni Física I – UTN – FRC
2
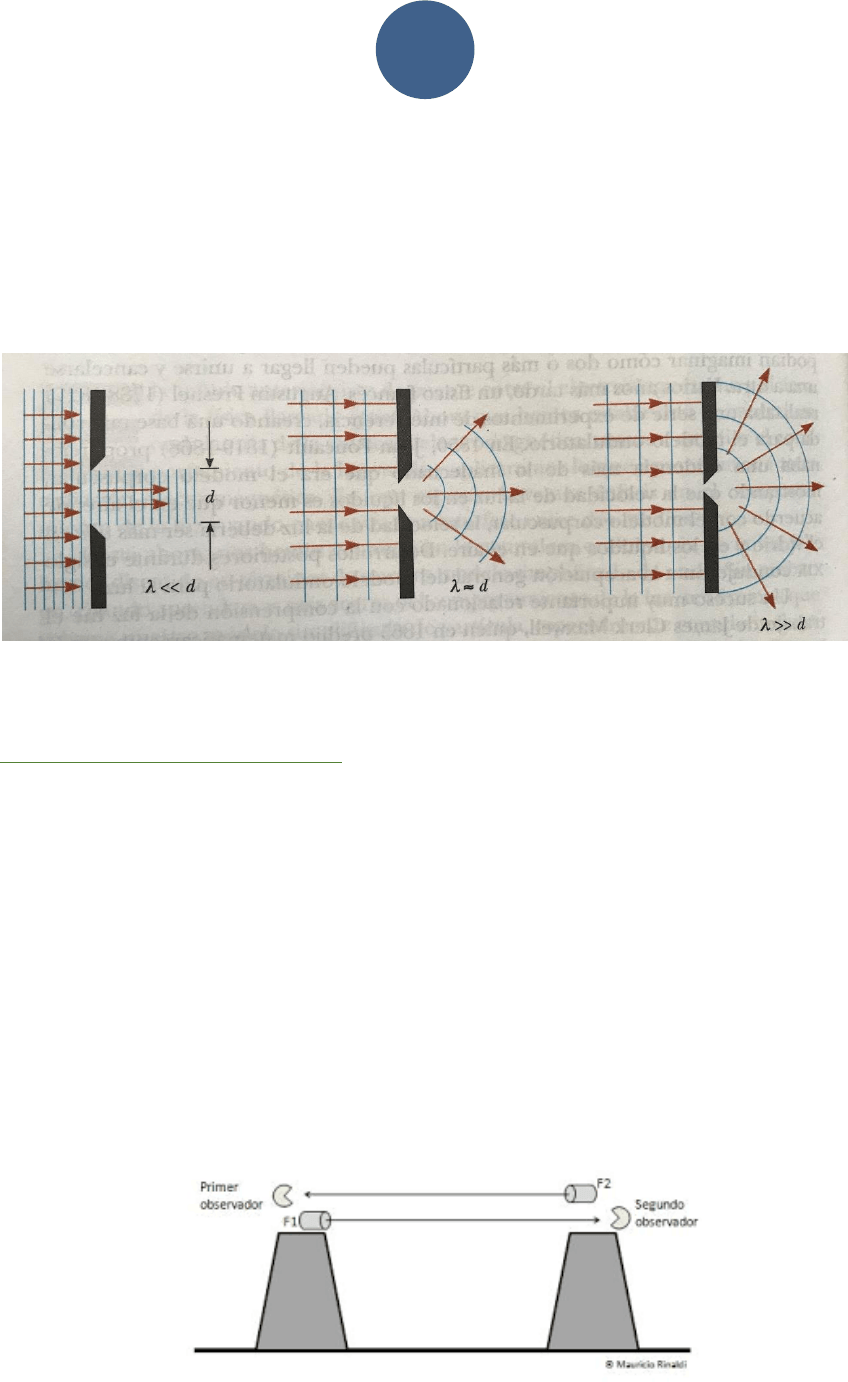
Entonces, la Óptica Geométrica es un tratamiento aproximado en el cual las ondas
electromagnéticas se pueden representar por rayos rectos. Este es el “Modelo de
Rayos” de la Óptica Geométrica. Por cierto, será válido si las ondas no encuentran
obstáculos comparables en tamaño, con la longitud de onda de la radiación. En ese
sentido, la condición óptima es que , en donde tamaño del orificio. De lo
contario se desprenden conceptos como: Interferencia, Polarización y Difracción; que
son fenómenos físicos que ahora no estudiaremos.
Mediciones de la rapidez de la luz:
La rapidez de la luz es muy alta y en vacío vale
.
Esto hizo que los primeros intentos para medirla no fueran exitosos…
A finales del 1700, Galileo intentó calcularla y para ello colocó a dos observadores en
dos torres separadas una distancia de 5 (millas). Cada observador tenía una linterna. Por
lo tanto al encender una de ellas, el otro al ver la luz encendería la suya. El intento
fracasó por dos motivos: a) debido a que el tiempo que se medía en relación al viaje de
ida y vuelta de la luz de una torre a otra, incluía también los tiempos de reacción de
ambos observadores, y b) la distancia entre las torres resultaba muy pequeña teniendo
en cuenta que la rapidez a la que se propaga la luz en el aire es muy alta.
Quienes obtuvieron por primera vez un valor aproximado de la rapidez de la luz, fueron
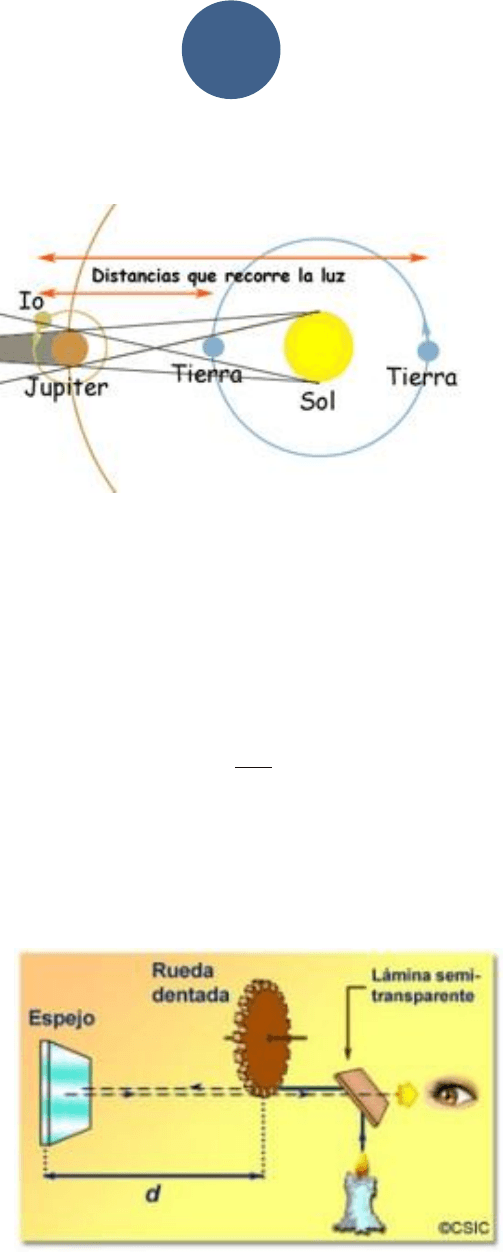
Roemer y Huygens. La técnica de Roemer (1644 – 1710) consistió en hacer
observaciones astronómicas de una de las lunas de Júpiter, llamada Io. Al valor de la
Ing. Juan Lancioni Física I – UTN – FRC
3
rapidez de la luz lo calculó finalmente Huygens con los datos de Roemer y le dio
. Un valor finito!
Corría el año 1849 cuando Fizeau, calcula por primera vez, un valor de la rapidez de la
luz muy parecido al que se conoce en la actualidad. La idea fue medir el intervalo de
tiempo que le toma a luz viajar desde algún punto hasta un espejo y regresar a dicho
punto, experiencia esta, muy parecida a la de Galileo. Si “d” es la distancia entre la rueda
dentada y el espejo plano y, “t” es el tiempo de viaje completo (ida y vuelta), la rapidez
de la luz se pudo calcular como:
y el valor obtenido fue de
, ya mucho más cercano al actual!
Nota: más detalles de cada uno de estos experimentos y otros más, podrá tomarlos
desde cualquier texto de física o desde una página de internet confiable.
En la actualidad el perfeccionamiento de la técnica de Fizeau, permitió finalmente
determinar que la rapidez de la luz en el vacío es
y en el aire
aproximadamente ese valor.
Ing. Juan Lancioni Física I – UTN – FRC
4
Fenómenos de Reflexión y Refracción:
Reflexión de la Luz
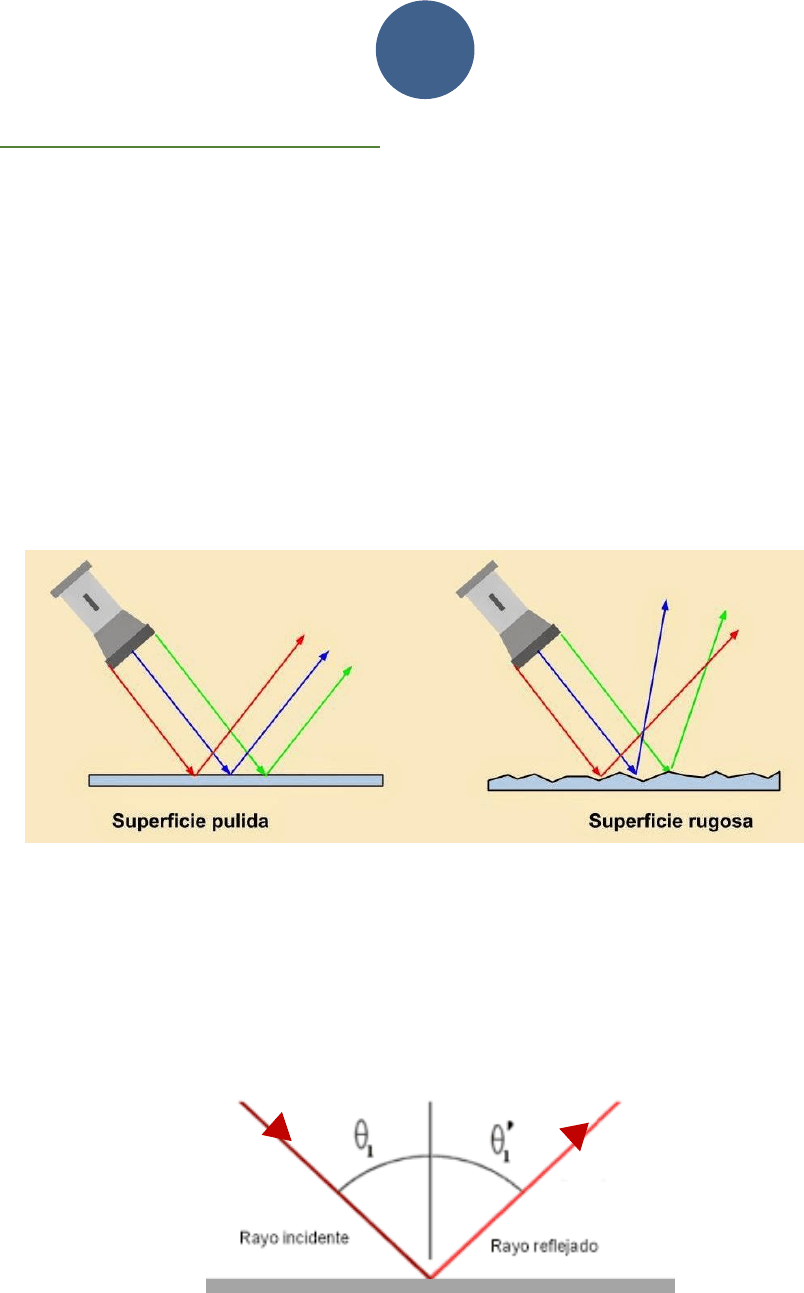
Cuando un rayo de luz se propaga de un medio a otro, parte del rayo incidente se refleja
en el primer medio y parte se refracta. La
figura (a) muestra algunos rayos incidentes
que se reflejan en una superficie lisa, similar a un espejo plano. Los rayos reflejados son
todos paralelos entre sí. Esto fenómeno se conoce como reflexión especular o
simplemente reflexión. Por otra parte, si la superficie reflectora es rugosa, como la
figura (b), los rayos reflejados tendrán distintas orientaciones y a esta situación se la
denomina reflexión difusa.
figura (a) figura (b)
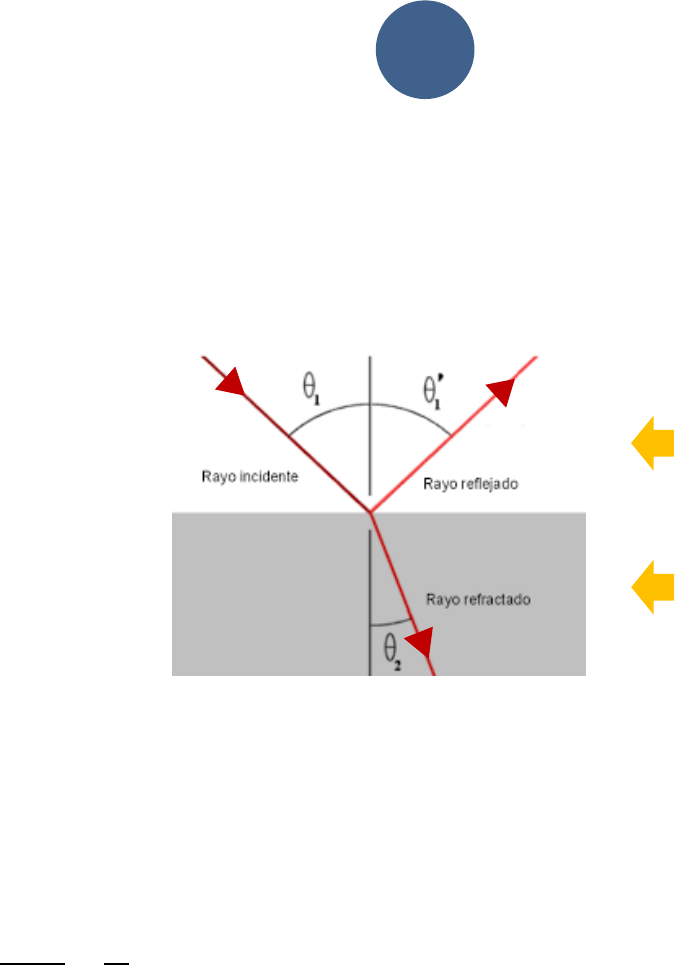
Supongamos ahora un rayo de luz que se propaga por el aire y que incide, con una cierta
inclinación, sobre una superficie plana y lisa (como por ejemplo un espejo). Los rayos
incidente y reflejado, forman ángulos
con la normal a la superficie y, a través de
distinto experimentos se demostró que el ángulo de incidencia es igual al ángulo de
refracción.
Entonces en la Ley de Reflexión se escribe que:
(1)
Normal
Ing. Juan Lancioni Física I – UTN – FRC
5
Luz Refractada
Cuando un rayo que se propaga a través de un medio trasparente se topa con una frontera que
conduce a otro medio también trasparente, parte del rayo se refleja, según lo explicado en el
párrafo anterior y, otra parte ingresa al segundo medio. El rayo que entra al otro medio se desvía
en la frontera y entonces se afirma que hay Refracción. Veamos la siguiente figura:
De acá se desprenden los siguientes conceptos:
1.- El rayo incidente, reflejado y refractado están todos en un mismo plano.
2.- El ángulo de refracción
depende de las propiedades de los medios y del ángulo de
incidencia
. Esta dependencia se expresa como:
(2)
donde:
Quien descubrió experimentalmente esta relación fue Snell (1591 – 1627), de ahí que la
Ley de Refracción lleve su nombre. Más adelante retomaremos
(2) y la expresaremos en
términos del índice de refracción de cada uno de los medios.
3.- Los rayos de incidencia, reflexión y refracción se medirán siempre respecto de la
normal.
4.- La trayectoria de un rayo de luz a través de una superficie refractora es reversible.
5.- Cuando se pasa de un medio menos refringente a otro más refringente, el rayo
refractado se acerca a la normal y viceversa. Las figuran siguientes ilustran lo que se
acaba de expresar.
Normal
medio 1
medio 2
Ing. Juan Lancioni Física I – UTN – FRC
6
Tener en cuenta que:
. Este último
dependiendo del tipo de vidrio.
Índice de Refracción y su relación con la Ley de Snell:
Sabemos que la luz en el vacío viaja a
y disminuye su rapidez cuando
atraviesa algún material. Debido a esto, se propone definir al índice de refracción como:
(3)
De esta manera se pudo tabular el valor de los índices de refracción de ciertas sustancias
transparentes, gases, líquidos y sólidas, medidos con luz amarilla de sodio de longitud
de onda , que se muestran a continuación:
Ing. Juan Lancioni Física I – UTN – FRC
7
Según la definición expresada en (3), se puede deducir que el índice de refracción es
adimensional y siempre mayor que 1, ya que la rapidez de la luz en un medio es siempre
menor que en el vacío.
A continuación, con las fórmulas
(2) y (3) y mediante formulaciones matemáticas,
expresaremos otra forma de la Ley de Snell, que es la más utilizada en ciencia e incluso
en las clases de resolución de problemas.
Veamos entonces; si de
(3) se despeja , se obtiene que:
y al adaptar esta expresión para cada uno de los medios, 1 y 2 respectivamente, se tiene:
entonces, si reemplazamos estas dos últimas expresiones en (2), nos queda:
que, simplificando “c” y haciendo el producto de los extremos por los medios en el
segundo miembro, se llega a:
Lo que finalmente, despejando da:
(4)
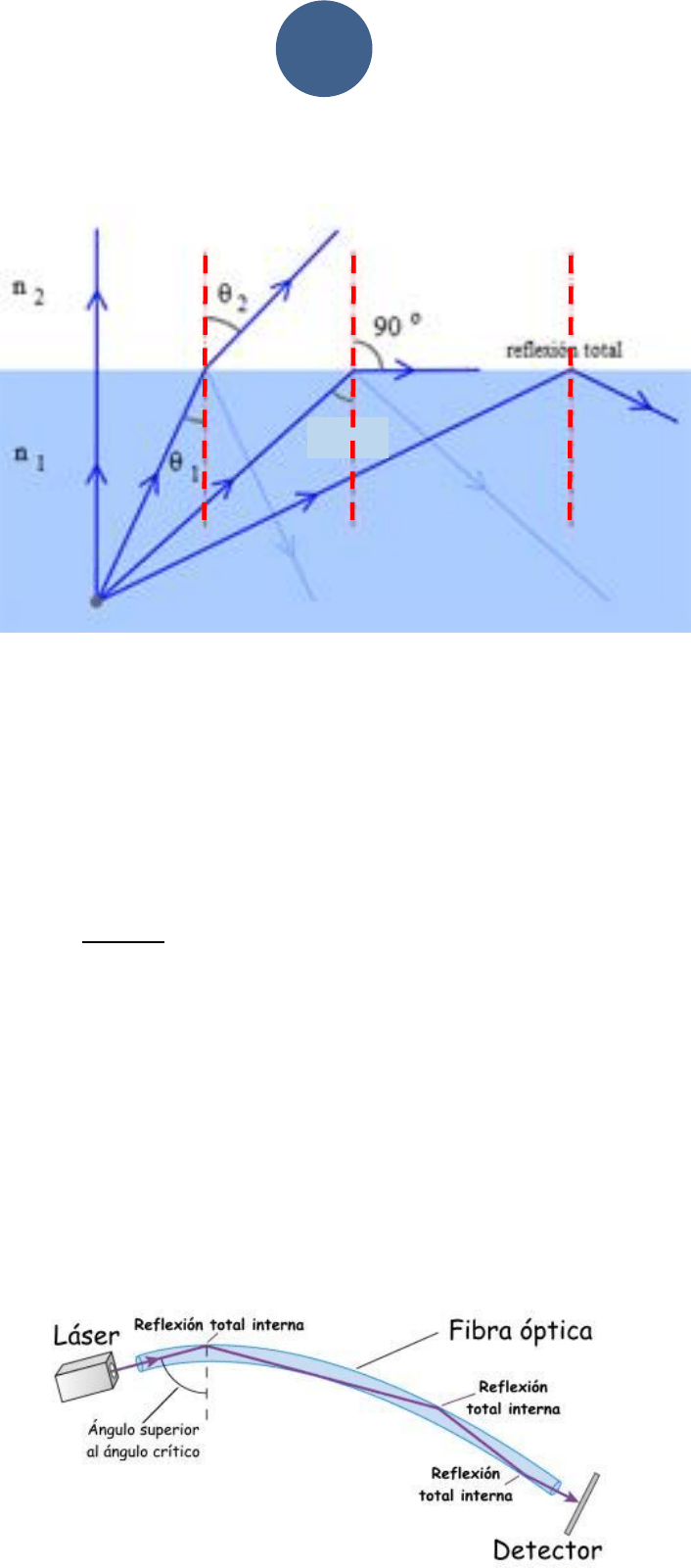
Reflexión Interna Total:
Este fenómeno físico ocurre cuando un rayo de luz pasa de un medio más refringente a
otro menos refringente, como por ejemplo del agua al aire, del vidrio al aire, etc.
El rayo incidente podrá tomar distintas inclinaciones respecto de la normal “N” en donde
se irá refractando hacia el segundo medio que es el aire, pero, ocurrirá que para un
Ing. Juan Lancioni Física I – UTN – FRC
8
ángulo crítico el rayo refractado emergerá paralelo a la superficie que divide a ambos
medios, es decir con un ángulo
.
Si se aplica la Ley de Snell en esa situación, se puede calcular el ángulo incidente crítico.
En el ejemplo agua-aire ese ángulo crítico será de:
.
Esta cuenta se hace despejando:
(5)
y reemplazando los valores de:
intente hacerlo y lo confirmará!
Entonces si usted opera ahora con ángulos superiores a
ocurre el fenómeno
de Reflexión Interna Total, es decir que los rayos incidentes ya no se refractan más hacia
el segundo medio: aire, sino que se reflejan y permanecen en el primer medio: agua.
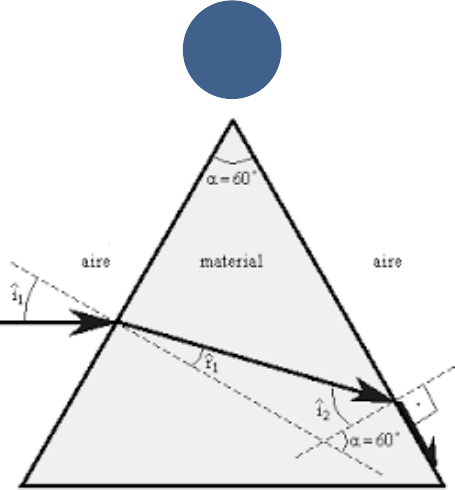
Hay muchos ejemplos interesantes en donde se aplica este fenómeno de la Óptica
Geométrica, no obstante lo invito a que lea e interprete el de fibra óptica y primas en
general. Algunos de estos casos van a ser resueltos en clase de problemas.
Ing. Juan Lancioni Física I – UTN – FRC
9
Es todo!!! Luego en el Práctico se resolverán algunos problemas y usted se empezará a
sentir más seguro con estos temas.
Le deseo éxitos en su estudio. Hasta la próxima!!!
Ing. Juan Lancioni.
OPTICA_GEOMÉTRICA_-_NATURALEZ_DE_LA_LUZ_-_REFLEXION_Y_REFRACCIÓN_-_RIT.pdf
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.