MATEMÁTICAS
MATEMÁTICAS
LOS NÚMEROS REALES
GENERALIDADES
Definición: Los números reales son todos aquellos que
encontramos en el mundo real como resultado del acto de
medir, calcular o modelar situaciones de nuestro entorno
natural o artificial. Se simboliza con la letra R y se puede
representar en notación de intervalo como: (-∞,+∞)= R
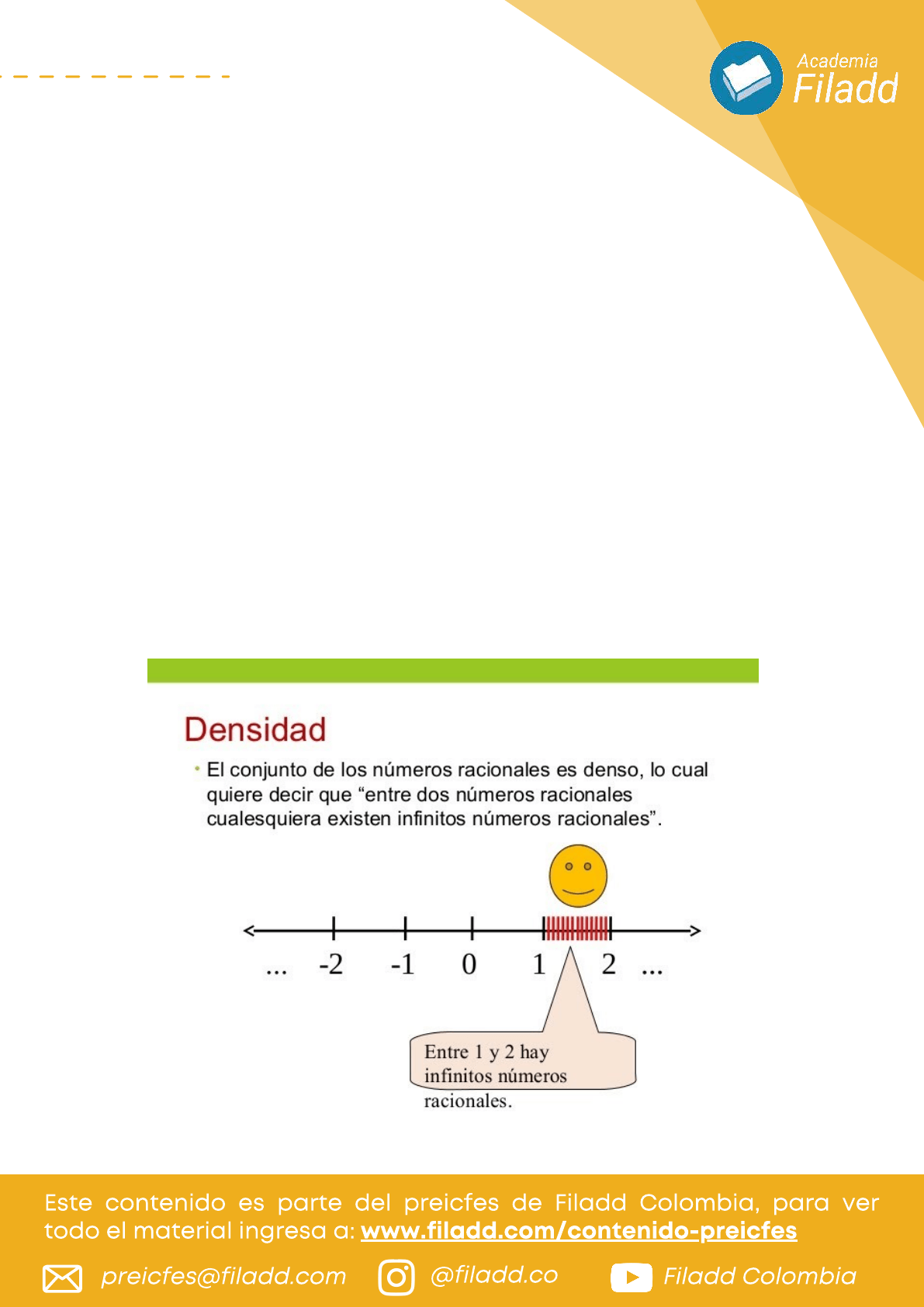
Densidad: Entendiendo la recta numérica como una sucesión
infinita de puntos, se establece que cada punto de la recta
corresponde a un número real, de modo que entre cada par de
números reales siempre hay infinitos números reales.
MATEMÁTICAS
un procedimiento interesante en matemáticas permite
calcular uno de esos infinitos valores entre dos números
reales “a” y “b”. Hablamos del valor medio entre los
números “a” y “b”. Se calcula mediante la semisuma de
dichos números, así:
(a+b)/2 intenta hallar valor medio entre los dos
números reales dados en cada caso:
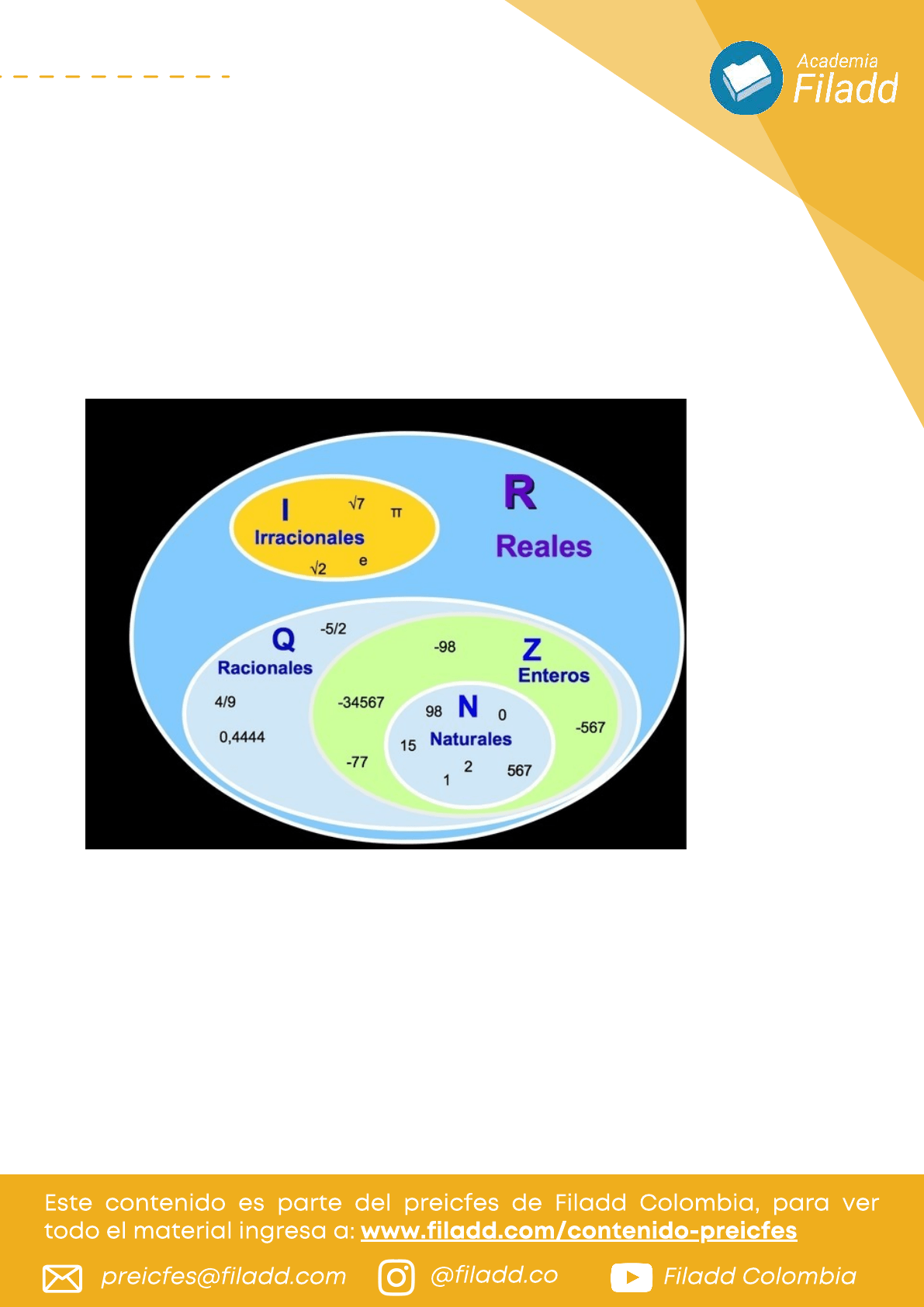
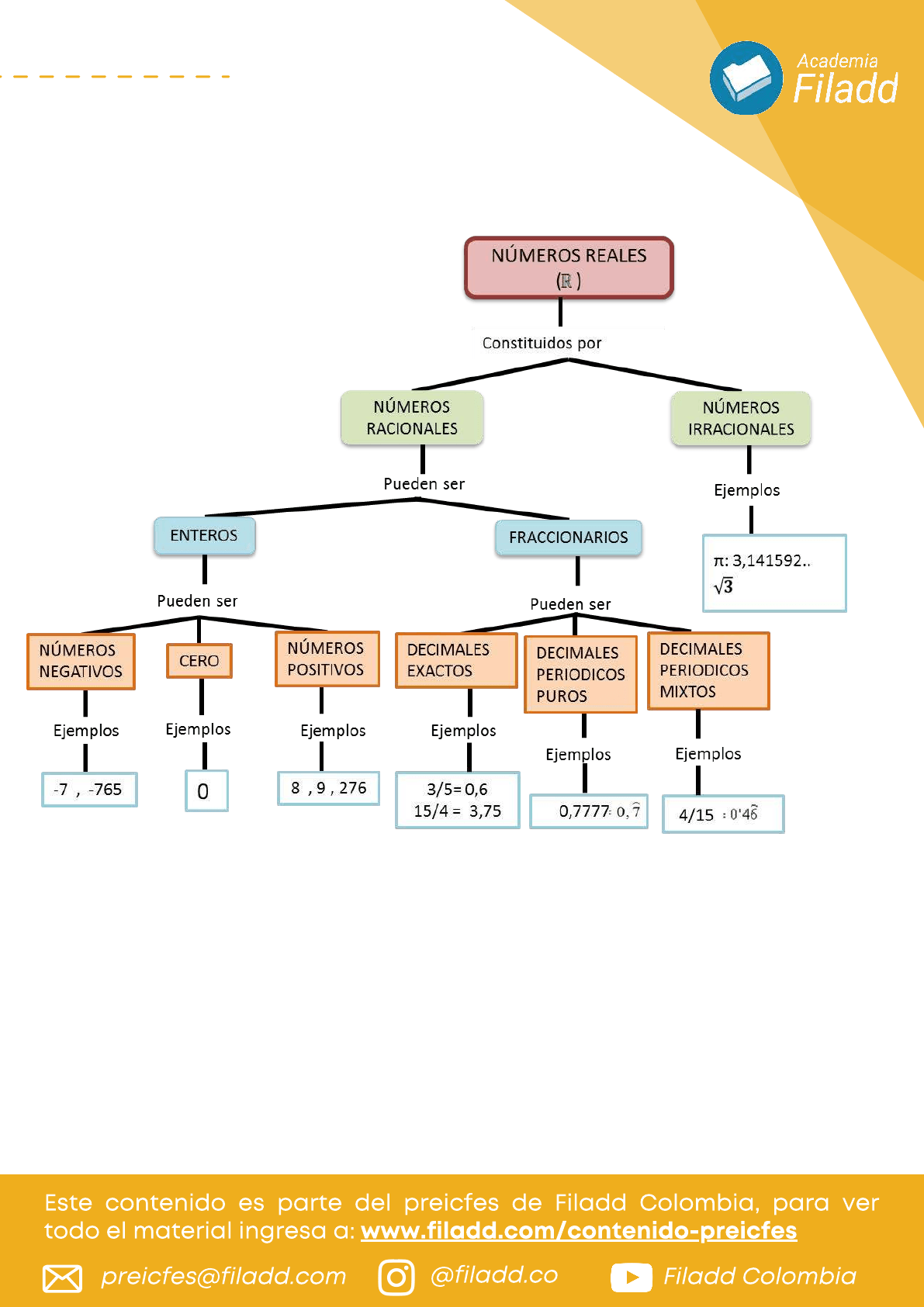
Subconjuntos numéricos: El super conjunto de los números
reales comprende los conjuntos de los números naturales, los
enteros, los racionales y los irracionales.
Naturales: son todos aquellos números que usamos
naturalmente al contar. Al contar los elementos de un
conjunto (ovejas de un rebaño, sillas en la casa, invitados a
una fiesta) decimos expresiones como uno, dos, tres, cuatro,
cinco o incluso cero elementos. Dichas expresiones
corresponden al significado cardinal de número natural. Pero
no se queda ahí. También podríamos usar el significado
ordinal de número natural mediante el cuál expresamos:
primero, segundo, tercero, etc. Incluso existen otros
contextos como el de medida, código o ubicación.
MATEMÁTICAS
Se puede o no considerar como primer elemento de este
conjunto al número cero, a partir del cual se generan
incrementos sucesivos de una unidad sin llegar a tener
fin. Se simbolizan con la letra N y se representan así:
N = {0, 1, 2, 3, 4, ...+∞ }
Enteros: Si observamos la representación de los números
naturales, estos se extienden hacia el lado derecho de la
recta, pero y ¿Qué se encuentra hacia el lado izquierdo?
Entre otros números, los dichosos números enteros
negativos que junto con el cero y los mismos naturales
(enteros positivos), forman el conjunto de los números
enteros, simbolizados con la letra Z. Ver imagen
MATEMÁTICAS
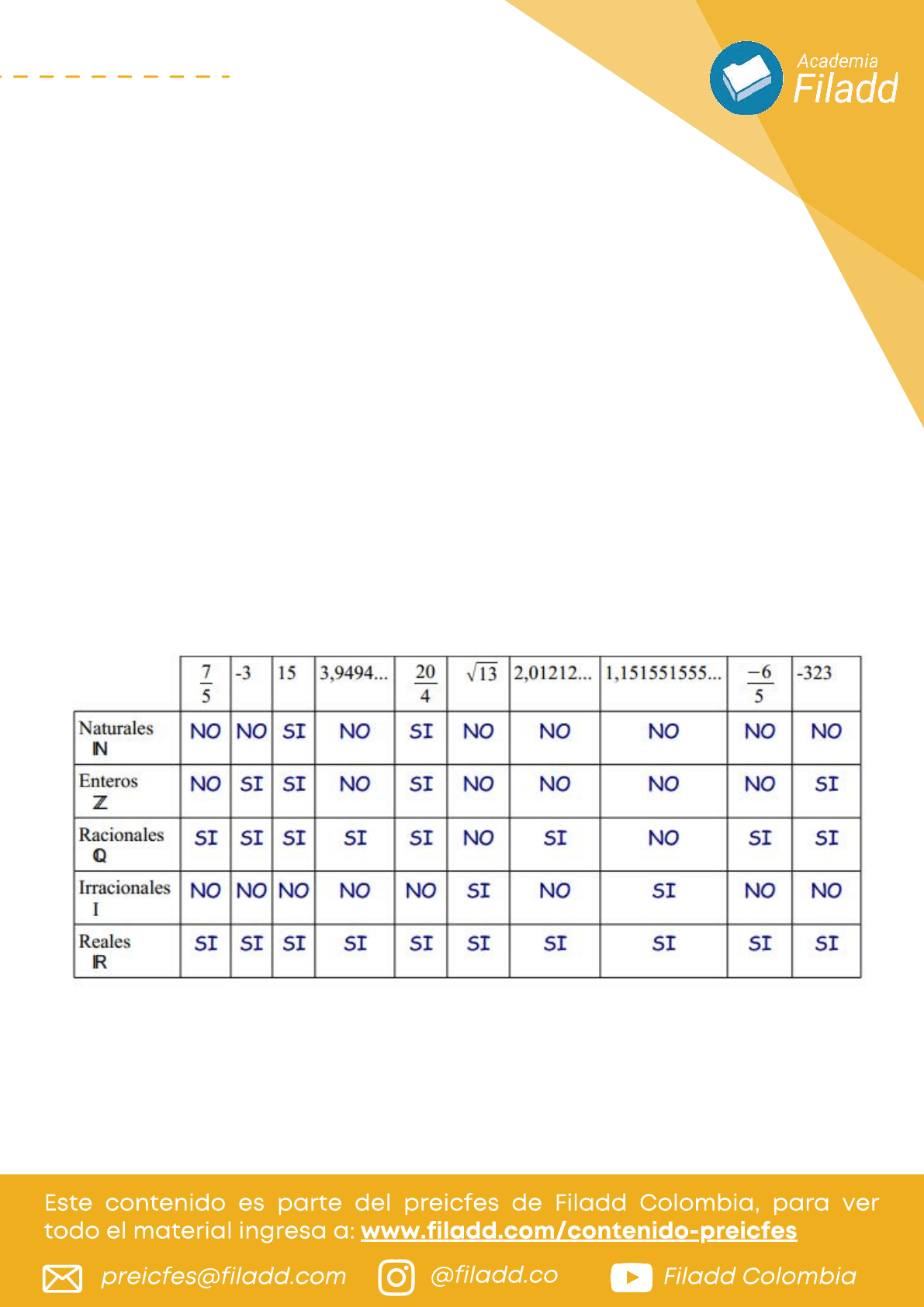
Número Racional: Es cualquier número que se pueda escribir
como una fracción. Entendiendo que una fracción es a su vez
la relación entre dos números enteros. Los números
racionales pueden ser naturales, enteros, decimales siempre
que correspondan al cociente de una fracción. Símbolo de los
números racionales: Q (por cociente en inglés)
Ejemplos: 2/5 es racional porque es fracción; -3 es racional
porque al ser entero, puede escribirse -3/1 sin alterar su valor
y viéndose como fracción; 2,5 es racional porque al ser
decimal finito, es cociente de alguna fracción, en este caso,
25/10.
En resumen, podemos definir un número racional así:
MATEMÁTICAS
Es de esta manera que la recta numérica se va tornando cada
vez más densa, a medida que sus espacios van siendo llenados
con la diversidad de números que van apareciendo
Números Irracionales: Aquí completamos los subconjuntos
numéricos de los número reales. Resulta que no todo número
es posible representarlo como fracción. Es decir, no todo
número es racional, en este caso, es cuando se denomina
justamente, Irracional. Es decir, números que siendo
decimales infinitos no periódicos jamás serán el cociente de
dos enteros y que merecen un estudio especial. Los más
famosos son pi, Euler y fi que se simbolizan con las letras π, e
y ϕ, respectivamente.
Números reales - Matemáticas Prueba Saber 11 ICFES.pdf
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.