MODELO 1 - SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 1
¿En qué se diferencia principalmente una
prueba de hipótesis sobre una media que
tiene varianza poblacional conocida de otra
que tiene la varianza poblacional
desconocida?
a. En las hipótesis estadísticas.
b. En el estadístico de prueba.
c. En el nivel de significación.
d. En el error de tipo II.
PREGUNTA 2
¿Cuál de las siguientes afirmaciones supone
la existencia de una correlación lineal
inversa perfecta entre dos variables?
a. Los puntos del diagrama de dispersión
están alineados en una recta decreciente.
b. Los puntos del diagrama de dispersión
están alineados en una recta creciente.
c. El coeficiente de correlación de Pearson
muestra un valor de r exactamente igual a
1.
d. El coeficiente de correlación de Pearson
muestra un valor de r exactamente igual a
0.
PREGUNTA 3
La variable del modelo binomial es
cuantitativa…
a. continua, con valores entre -∞ y +∞.
b. discreta, con dos valores o más.
c. continua, con valores iguales o mayores a
0.
d. discreta, con únicamente dos valores.
PREGUNTA 4
Considere las características de la
distribución normal unitaria. La probabilidad
de que z sea mayor o igual a -0.8, en
términos simbólicos P (z ≥ -0.8), es igual a la
probabilidad…
a. P (z ≤
0.8).
b. P (z ≥ 0.8).
c. P (z ≥ -0.2).
d. P (z ≤
0.2).
PREGUNTA 5
En un estudio sobre los efectos de la terapia
cognitiva en la reducción de la ansiedad se
llevó a cabo un contraste de hipótesis. Se
compararon los niveles de ansiedad antes y
después del tratamiento en un grupo de 30
pacientes seleccionados de manera
aleatoria. Si el valor p obtenido en la prueba
fue de 0.025 ¿cuál sería la conclusión
apropiada para un nivel de significación del
1%?
a. Aceptar la hipótesis nula y concluir que no
hay evidencia suficiente para afirmar que
esta terapia cognitiva reduce la ansiedad.
b. Rechazar la hipótesis nula y concluir que
hay evidencia suficiente para afirmar que
esta terapia cognitiva reduce la ansiedad.
c. No se puede tomar una decisión
concluyente con una muestra tan
pequeña. Se requieren más
investigaciones.
d. Rechazar la hipótesis nula y concluir que
no hay diferencias significativas en los
niveles de ansiedad antes y después del
tratamiento.
PREGUNTA 6
En un estudio epidemiológico realizado en
la ciudad de Rosario se encontró que los 24
adolescentes de una muestra aleatoria
habían consumido sustancias psicoactivas,
en promedio, 4.5 veces por semana. Sin
embargo, según los estudios de los últimos
años esta población de jóvenes presentaba
una media de frecuencia de consumo
semanal de 3 veces. Los profesionales
necesitan saber si deberían alarmarse por
estos resultados. ¿Cómo deberían plantear
las hipótesis en un contraste?
a. H0: µ ≥ 3 y H1: µ < 3.
b. H0: µ ≤ 3 y H1: µ > 3.
c. H0: µ ≥ 4.5 y H1: µ < 4.5.
d. H0: µ ≤ 4.5 y H1: µ > 4.5.

MODELO 1 - SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 7
La estatura promedio en una población de
mujeres se distribuye normalmente con
media 165 cm y desvío estándar de 5 cm. Se
desea extraer al azar una mujer de la
población. Lo más probable es que la
estatura de la mujer esté entre… (compare
las opciones y responda):
a. 175 y 180 cm.
b. 150 y 155 cm.
c. 170 y 180 cm.
d. 155 y 165 cm.
PREGUNTA 8
Una psicóloga implementó un grupo de
reflexión dirigido a licenciadas en obstetricia
con el objetivo de mejorar sus habilidades
comunicacionales, bajo la premisa de que
dichas habilidades son importantes para
aumentar el bienestar de las embarazadas
durante el parto. Para probar su premisa, se
seleccionaron al azar 50 licenciadas que
trabajan en hospitales públicos de CABA y
luego se las asignó aleatoriamente en dos
grupos. Un grupo participó de un dispositivo
semanal tendiente a mejorar las habilidades
comunicacionales, mientras que el otro
grupo se usó como control. Transcurridos 6
meses, las participantes respondieron una
prueba que evalúa habilidades
comunicacionales. La aplicación de una
prueba de hipótesis en el análisis de estos
datos registró un valor p de 0.003.
Señale la afirmación correcta:
a. Se utilizó un estadístico de prueba que se
distribuye según el modelo t de Student
con 49 grados de libertad.
b. La investigadora puede rechazar la
hipótesis nula tanto si usa un alfa de 0.05
como si usa un alfa de 0.01.
c. La H1 afirma que el grupo que participó
del dispositivo registró mayores niveles
de bienestar en las embarazadas que
acompañaron durante el parto.
d. Se aplicó una prueba de hipótesis para la
diferencia de medias de dos muestras
apareadas.
PREGUNTA 9
Cuanto más extremo resulta el estadístico de
prueba…
a. más pequeño será el alfa.
b. más grande será el alfa.
c. más pequeño será p.
d. más grande será p.
PREGUNTA 10
Un alumno cargó estos datos en la
aplicación de la cátedra para calcular una
probabilidad:
Sabiendo que la variable binomial de su
ejercicio es: “Cantidad de personas con
disfunción neurológica en una muestra de
cuatro pacientes adultos mayores
seleccionados al azar en el hospital de
Morón” y tiene un parámetro p = 0.2. ¿Cuál
de las siguientes afirmaciones es correcta?
a. La probabilidad de que un paciente de los
cuatro seleccionados presente disfunción
neurológica es de 0.2.
b. La probabilidad de que un adulto mayor
seleccionado al azar en la población
tenga disfunción neurológica es de
0.4096.
c. La probabilidad de que un paciente de los
cuatro seleccionados presente disfunción
neurológica es de 0.4096.
d. La probabilidad de que por lo menos un
paciente de los cuatro seleccionados
presente disfunción neurológica es de
0.4096.

MODELO 2 - SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 1
La probabilidad de rechazar a la hipótesis
nula de acuerdo al valor del estadístico de
prueba obtenido en el contraste recibe el
nombre de:
a. Error de tipo I.
b. Valor p.
c. α.
d. β.
PREGUNTA 2
Gracias al teorema de tipificación es posible
concluir que en una variable que se
distribuye normalmente:
a. Coinciden las tres medidas de tendencia
central: media, mediana y moda.
b. Existen dos puntos de inflexión en donde
cambia la concavidad de la curva.
c. A medida que los valores se alejan de la
media son cada vez menos probables.
d. La probabilidad acumulada hasta la
media µ coincide con la probabilidad
acumulada hasta z = 0.
PREGUNTA 3
Considere un examen breve que evalúa el
conocimiento sobre un tema usando sólo 4
preguntas de 4 opciones de respuestas en
donde una es correcta. La variable cantidad
de respuestas correctas en este examen
suponiendo que los alumnos respondan al
azar sigue una distribución binomial, por lo
que se cargaron los siguientes datos en la
app de la cátedra:
En este planteo, 0,2109 es la probabilidad de
acertar por azar…
a. a la mitad de las preguntas del examen.
b. a una de las preguntas del examen.
c. a más de la mitad de las preguntas del
examen.
d. al 25% de las preguntas del examen.
PREGUNTA 4
Al comenzar una prueba de hipótesis, la
hipótesis nula…
a. determinará si el contraste es uni o
bilateral.
b. define qué evidencia empírica se tomará
en cuenta.
c. debe asumirse verdadera, aunque luego
se rechace.
d. define la regla de decisión.
PREGUNTA 5
Las investigaciones sobre consumo de
tabaco en población adolescente informan
que estos individuos consumen, en
promedio, 5,3 cigarrillos diarios. Las
autoridades de un colegio realizaron un
estudio a partir de una selección aleatoria de
24 adolescentes de la institución y
registraron que la cantidad media fue de 5,
con una desviación estándar de 0,13. Con
esta información realizaron una prueba de
hipótesis para determinar si sus estudiantes
consumen menos cigarrillos que la
población y obtuvieron un estadístico de
prueba de -2.23 con un valor p de 0,018.
¿Cuál de estas afirmaciones es correcta?
a. Realizaron un contraste basándose en la
hipótesis nula H0: µ ≥ 5.
b. Llevaron a cabo un contraste sobre una
media con varianza poblacional conocida.
c. La diferencia entre las medias 5,3 y 5 es
despreciable como para considerarla
significativa.
d. Es posible que cometan un error de tipo II
si toman un nivel de significación del 1%.
PREGUNTA 6
La edad del primer embarazo se distribuye
normalmente con media 30 y desvío 10
años en una determinada población. Los
especialistas consideran que una edad
inferior a 15 o superior a 45 años puede
considerarse riesgosa para madres
primerizas. ¿Cuál de las siguientes
expresiones permite calcular la
probabilidad de que una persona
pertenezca al grupo de riesgo?
a. P (15 ≤ X ≤ 45).
b. P (-1 ≤ Z ≤ 1).
c. 1 – P (15 ≤ X ≤ 45).
d. P (10 ≤ X ≤ 30).
MODELO 2 - SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 7
En una investigación se encontró un
coeficiente de correlación r = -0.90 entre el
puntaje en una escala de motivación ante la
tarea y la cantidad de errores cometidos por
falta de concentración. Este resultado
permite concluir que:
a. Los puntajes elevados de motivación son
la causa de los problemas de
concentración.
b. Cuanto más altos resultaron los puntajes
de motivación, más errores de
concentración se registraron.
c. Cuanto más elevados resultaron los
puntajes de motivación, se registraron
menos errores de concentración.
d. Los errores de concentración se explican
por los altos puntajes de motivación.
PREGUNTA 8
Desde el Ministerio de Educación se diseñó
un programa de intervención para mejorar el
rendimiento en lectoescritura de los niños.
Para ponerlo a prueba seleccionaron al azar
a una muestra de 300 niños y aplicaron el
programa durante 8 semanas. Luego
evaluaron a estos alumnos, obteniendo una
calificación promedio de 40 puntos. Si se
sabe que los puntajes en la población de
niños escolarizados en esta evaluación se
distribuyen normalmente con media 38.9
puntos con un desvío estándar de 5 puntos,
sería posible realizar un contraste de
hipótesis sobre:
a. Una media con varianza poblacional
conocida, con H1: µ > 38.9.
b. Una media con varianza poblacional
desconocida, con H1: µ > 40.
c. La diferencia de medias de dos
poblaciones relacionadas, con H1: µ
D
> 0.
d. La diferencia de medias de dos
poblaciones independientes, con H1:
µ
Población
- µ
Muestra
> 0.
PREGUNTA 9
El valor máximo que puede tomar una
variable binomial siempre será:
a. 1.
b. +∞.
c. n + 1.
d. n.
PREGUNTA 10
Un equipo del Hospital Gosset administró a
una muestra de 16 pacientes cardíacos un
test que mide el nivel de enojo y obtuvo una
media de 38 con un desvío de 10. Según los
registros del hospital previos a la pandemia,
la media de la población de este tipo de
pacientes era de 34 puntos. Al realizar una
prueba de hipótesis bilateral hallaron un
valor p igual a 0,044. Por lo tanto, la
información muestral recabada brinda
evidencia acerca de la existencia de:
a. Una diferencia estadísticamente
significativa en el puntaje medio de enojo
de la población de pacientes cardíacos
para un α = 0,025.
b. Un incremento estadísticamente
significativo en el puntaje medio de enojo
de la población de pacientes cardíacos
para un α = 0,05.
c. Una diferencia estadísticamente
significativa en el puntaje medio de enojo
de la población de pacientes cardíacos
para un α = 0,05.
d. Un incremento estadísticamente
significativo en el puntaje medio de enojo
de la población de pacientes cardíacos
para un α = 0,025.
MODELO 3 - SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 1
Se considera deterioro cognitivo leve
cuando la persona registra déficits
clínicamente significativos (más de 1,5
desvíos por debajo de la media) en una
prueba de memoria episódica cuyos
puntajes se distribuyen normalmente con
media de 28 y desvió estándar de 4. Se
desea calcular la probabilidad de que un
sujeto presente deterioro cognitivo leve
¿Cuál de las siguientes expresiones
permitiría calcular esta probabilidad?
a. P (X ≥ 24).
b. Ninguna opción es correcta.
c. P (Z ≤ 1,5).
d. P (X ≤ 22).
e. P (Z ≥ -1,5)
PREGUNTA 2
Estudios realizados en años anteriores
informan que de cada 10 niños porteños de
entre 6 y 12 años que inician una
psicoterapia, 6 lo hacen por haber sido
derivados por la escuela a la que asisten.
¿Qué datos debería ingresar a la aplicación
de la catedra si quiere calcular la
probabilidad de que el 25% de los sujetos
dentro de una muestra aleatoria de 24 niños
provenientes de esa población hayan sido
derivados a psicoterapia por la escuela?
a. Valor de n: 10
Valor de p: 0.6
Éxitos de prueba: 5
Probabilidad = 0.2007.
b. Valor de n: 24
Valor de p: 0.25
Éxitos de prueba: 6
Probabilidad = 0.1853.
c. Valor de n: 24
Valor de p: 0.6
Éxitos de prueba: 6
Probabilidad = 0.0004.
d. Valor de n: 10
Valor de p: 0.25
Éxitos de prueba: 5
Probabilidad = 0.0584.
PREGUNTA 3
Un investigador sabe que la población de
personas con diagnóstico de adicción al
tabaco consume, en promedio, 20 cigarrillos
diarios. El profesional desarrollo un
tratamiento para disminuir el consumo de
cigarrillos y quiso demostrar su efectividad
considerando una muestra aleatoria de 20
pacientes. Al plantear su contraste de
hipótesis el investigador definió la variable
del problema como X: "Cantidad diaria de
cigarrillos consumidos por…"
a. la población de individuos consumidores
de tabaco.
b. un paciente con adicción al tabaco
elegido al azar de un total de 20.
c. un paciente con adicción al tabaco
después del tratamiento.
d. una persona de la población de adictos al
tabaco.
PREGUNTA 4
En una prueba de hipótesis se compara el
nivel de depresión de pacientes con
trastorno de ansiedad generalizada (TAG) y
pacientes con trastorno bipolar (TB). Luego
de rechazar la hipótesis nula se pudo
confirmar que la diferencia entre las medias
es estadísticamente significativa. Esto puede
interpretarse como:
a. la muestra de pacientes con TAG tuvo
una media en depresión similar a la
observada por la muestra con TB.
b. no hay evidencias suficientes para afirmar
que los pacientes con TAG y TB
pertenecen a las poblaciones diferentes
con su respecto a su nivel de depresión.
c. se puede afirmar que los pacientes con
TAG y TB pertenecen a diferentes con
respecto a su nivel de depresión.
PREGUNTA 5
¿Cuál de las siguientes sentencias sobre
una hipótesis estadística es correcta?
Una hipótesis estadística puede ser una
afirmación…
a. que se realiza sobre una muestra para
sacar conclusiones sobre la población.
b. acerca del valor de uno o dos estadísticos
muestrales con distribuciones conocidas.
c. sobre la diferencia entre los parámetros
de las distribuciones de dos poblaciones.
d. verificable directamente para contrastarla
con la hipótesis científica.
MODELO 3 - SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 6
Una investigadora está interesada en
demostrar que los estudiantes de
arquitectura no difieren en su nivel de
razonamiento espacial con respecto a los
estudiantes de ingeniería. Seleccionó una
muestra aleatoria de estudiantes de
arquitectura, les aplicó un test de
razonamiento espacial y obtuvo una media
de 12 con un desvió estándar de 5. Además,
ella sabe que los puntajes de ese test se
distribuyen normalmente con media 13 y
desvió estándar 6 en un grupo normativo de
estudiantes de ingeniería.
La investigadora realizo un contraste de
hipótesis y como resultado de este estudio
rechazo la hipótesis para un nivel de
significación del 1%. Señale la opción
correcta:
a. la conclusión de este estudio es que los
estudiantes de arquitectura presentan un
mayor nivel de razonamiento espacial que
los estudiantes de ingeniería.
b. la conclusión de este estudio es que los
estudiantes de arquitectura presentan un
menor nivel de razonamiento espacial
que los estudiantes de ingeniería.
c. con su decisión la investigadora corre
riesgo de cometer error de tipo 2.
d. la presunción de la investigadora está
planteada en la hipótesis de contraste.
PREGUNTA 7
Se desea estudiar si existe algún tipo de
relación entre la edad paciente adulto y su
puntaje en una escala que mide su nivel de
depresión.
Sabiendo que se obtuvo un valor de r = 0.03
es posible afirmar que…
a. existe una asociación intensa entre
ambas variables.
b. la relación entre la edad y el nivel de
depresión es estadísticamente más
significativa para un nivel de significación
del 5%.
c. el 3% de los pacientes más jóvenes
también tienden a registrar puntajes bajos
de depresión.
d. la depresión del sujeto es completamente
independiente de su edad.
e. se descarta la existencia de una relación
lineal directa fuerte entre ambas
variables.
PREGUNTA 8
Suponga una variable X que se distribuye
normalmente con media µ y desviación típica
σ. Considere las siguientes opciones y
señale entre que valores de X se registra la
probabilidad más baja...
a. entre (µ + σ) y (µ + 2σ).
b. no es posible determinar la probabilidad
más baja a partir de la información
brindada.
c. entre (µ - σ) y (µ + σ).
d. entre µ y µ (µ - 2σ).
e. entre µ y (µ - σ).
PREGUNTA 9
Considere éxito terapéutico de un nuevo
tratamiento para el TAG como una variable
dicotómica (alcanzó/no alcanzó). Sea X una
variable binomial de parámetros n = 20 y p =
0.45 que se define a partir de la mencionada
variable dicotómica ¿cuál de las siguientes
afirmaciones seria INCORRECTA en este
caso?
a. La variable binomial es cuantitativa
discreta y puede tomar valores que
oscilan entre 0 y 20.
b. A nivel poblacional la probabilidad de
éxito terapéutico en el nuevo tratamiento
es igual a 0.45.
c. El éxito terapéutico en un individuo
modifica las posibilidades de éxito del
nuevo tratamiento en otro individuo dentro
de los 20 considerados.
d. La cantidad de pacientes que alcanzaron
el éxito terapéutico entre los 20 a los que
se les aplico el nuevo tratamiento para el
TAG tiene distribución binomial X ~ B (20;
0.45).
PREGUNTA 10
Si una prueba de hipótesis se decide
rechazar la hipótesis nula…
a. no se puede cometer error de tipo I ni de
tipo II.
b. Ninguna es correcta.
c. se puede cometer error de tipo I pero no
de tipo II.
d. se puede cometer ambos tipos de
errores.
e. se puede cometer error de tipo II pero no
de tipo I.

MODELO 4 – SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 1
PREGUNTA 4
Un equipo de profesionales pretende
administrar un Test de Ansiedad frente a los
exámenes en grupo de estudiantes de nivel
medio. Su objetivo es identificar a los
sujetos que presentan los niveles más
elevados de ansiedad para que participen de
un taller psicoeducativo.
Sabiendo que los puntajes del Test se
distribuyen según la normal unitaria y que
se convocaría a participar del taller a
quienes obtienen un puntaje mayor a 0,6,
¿qué porcentaje de estudiantes sería
esperable que sean convocados?
Considere estos resultados obtenidos con la
Aplicación de la materia. Identifique aquellos
que le sirven para responder y descarte los
datos irrelevantes.
a.
72.57%
b.
40%
c.
27.43%
d.
25%
PREGUNTA 2
¿Qué efecto produciría sobre la curva
normal una disminución del valor del
parámetro μ (manteniendo constante el
valor de σ)?
a.
Se modificaría el valor de la asíntota.
b.
Dejarían de coincidir los valores de la
media y la moda de la distribución.
c.
La curva se desplazaría hacia la
izquierda.
d.
Se acortaría la distancia entre μ y μ - σ.
PREGUNTA 3
La distribución t de Student NO se utiliza en
las pruebas de hipótesis sobre…
a.
una media con varianza poblacional
conocida.
b.
una media con varianza poblacional
desconocida.
c.
una diferencia de medias para muestras
apareadas.
d.
una diferencia de medias para muestras
independientes.
En el modelo binomial, la modalidad de la
variable dicotómica a la que se le asigna una
probabilidad p…
a.
verifica el cumplimiento de una condición.
b.
siempre remite al éxito terapéutico.
c.
es mayor que la otra modalidad, a la que
se asigna 1 - p.
d.
suele considerarse como “0” porque tiene
una probabilidad nula.
PREGUNTA 5
Si un investigador decide adoptar un nivel
de significación de 0.01 en lugar de 0.05…
a.
aumenta la probabilidad de cometer el
error de tipo I.
b.
disminuye la probabilidad de rechazar
una H0 que en realidad es cierta.
c.
disminuye la probabilidad de cometer el
error de tipo II.
d.
aumenta la probabilidad de rechazar una
H0 que en realidad es cierta.
PREGUNTA 6
Se desea saber si las personas que
presentan Fobia Social utilizan en forma
diferente las redes sociales para vincularse
con otras personas. Sabiendo que la
población mundial de usuarios de Instagram
permanece en promedio 3 horas diarias
conectada a esta aplicación, un investigador
seleccionó una muestra aleatoria de
pacientes con diagnóstico de Fobia Social y
analizó la cantidad de horas diarias que
permanecían conectados a ella. Se obtuvo
un estadístico t de Student con gl = 29 igual
a 1.90 y un valor p = 0.034. Estos datos nos
llevan a concluir que…
a.
para un alfa de 0.05, la información
muestral recabada brinda evidencia
suficiente para sostener una diferencia
significativa en el tiempo empleado en
Instagram por los pacientes Fobia Social.
b.
para un alfa de 0.01, la información
muestral recabada brinda evidencia
suficiente para sostener una diferencia
significativa en el tiempo empleado en
Instagram por los pacientes Fobia Social.
c.
para un alfa de 0.05, la información
muestral recabada es insuficiente para
sostener la existencia de una diferencia
significativa en el tiempo empleado en
Instagram por los pacientes Fobia Social.
d.
para un alfa de 0.10, la información
muestral recabada es insuficiente para
sostener la existencia de una diferencia
significativa en el tiempo empleado en
Instagram por los pacientes Fobia Social.

MODELO 4 – SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 7
PREGUNTA 9
Se estudió la relación entre Rendimiento
académico y los niveles de Ansiedad cuyo
diagrama de dispersión para una muestra
pequeña se ilustra a continuación:
Según este diagrama, marque la afirmación
correcta entre las siguientes:
a.
Las variables no están relacionadas.
b.
Las variables están relacionadas de
modo no lineal.
c.
La correlación lineal entre las variables
tiene una intensidad elevada.
d.
La correlación lineal entre las variables
tiene sentido negativo.
PREGUNTA 8
En un informe desarrollado por los
profesionales del Hospital Gosset se publicó
el siguiente diagrama sobre la variable
Estado Civil con las modalidades: Soltero
(1), Casado (2), Divorciado (3) y Viudo (4). El
mismo se confeccionó a partir de una
muestra de 455 pacientes atendidos en el
último año. Supongamos que se extraen al
azar 5 pacientes ¿cómo se determina la
probabilidad de que ninguno sea viudo?
a.
Como X~B (5; 0,75); entonces P(X = 0).
b.
Como X~B (4; 0,25); entonces 1-P(X = 0).
c.
Como X~B (5; 0,25); entonces P(X = 0).
d.
Como X~B (5; 0,25); entonces P(X ≥ 0).
Según una investigación realizada en 2002
sobre parejas divorciadas, el tiempo
promedio de duración de un matrimonio se
distribuye normalmente con una media de 12
años. Una profesional sospecha que este
valor está desactualizado. Su experiencia
como terapeuta de parejas le hace pensar
que la duración de los matrimonios es
actualmente menor. Decidió seleccionar una
muestra aleatoria de 35 parejas
recientemente divorciadas y registró una
media de 10 años de casados con un desvío
de 2 años. Los resultados le permitieron
confirmar su hipótesis para un nivel del 5%.
Señale la afirmación correcta:
a.
La hipótesis nula planteada para esta
investigación fue H0: μ ≤ 12.
b.
La profesional tiene un 95% de
probabilidad de estar cometiendo un error
de tipo II.
c.
El planteo supone un contraste unilateral
a derecha.
d.
El estadístico de prueba se distribuyó
según t de Student con 34 grados de
libertad.
PREGUNTA 10
Los profesionales del Hospital Gosset
decidieron analizar la eficacia de su
tratamiento y analizaron los resultados
obtenidos en el Grupo Tratamiento y en el
Grupo Control. Cada uno de estos grupos
fue evaluado antes y después del
tratamiento. Como esperaban, las pruebas
estadísticas realizadas les permitieron
concluir que los pacientes del Grupo
Tratamiento redujeron la sintomatología
mientras que en el Grupo Control no se
registraron diferencias significativas.
A partir de esto usted puede inferir que los
investigadores aplicaron…
a.
dos pruebas de diferencia de medias
para muestras independientes, una en
cada grupo.
b.
dos pruebas de diferencia de medias
para muestras apareadas, una en cada
grupo.
c.
una prueba de diferencia de medias para
muestras independientes en el Grupo
Control y una para muestras apareadas
en el Grupo Tratamiento.
d.
una prueba de diferencia de medias para
muestras independientes en el Grupo
Tratamiento y una para muestras
apareadas en el Grupo Control.
MODELO 5 – SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 4
PREGUNTA 1
El alfa y el valor p son probabilidades…
a.
que dependen del valor que adoptó el
estadístico de prueba en la muestra.
b.
relativamente pequeñas y determinadas
por el investigador.
c.
cuya localización depende del tipo de
contraste (unilateral o bilateral).
d.
vinculadas a las distribución muestral del
estadístico de contraste.
PREGUNTA 2
Suponga una variable que se distribuye
normalmente con media 10 y desvío 2. Un
investigador sabe que la probabilidad de
obtener un puntaje entre 12 y 14 es igual a la
probabilidad de obtener puntajes entre:
a.
6 y 8.
b.
4 y 6.
c. 10 y 12.
d. 14 y 16.
PREGUNTA 3
Un equipo está interesado en demostrar que
las personas ambidiestras alcanzan una
destreza equiparable en sus habilidades de
escritura si se compara el desempeño de
sus dos manos. Seleccionaron una muestra
aleatoria de 32 ambidiestros y les solicitaron
que escribieran una frase con la mano
derecha y luego otra frase con la mano
izquierda. Los investigadores registraron el
tiempo que tardó cada individuo en escribir
las frases y con estos datos calcularon la
variable D = X
DERECHA
– X
IZQUIERDA
para llevar
adelante el contraste de hipótesis para
muestras relacionadas. Basándose en la
evidencia empírica, los investigadores
rechazaron la hipótesis nula para un nivel de
significación del 1%.
Considerando el escenario planteado, ¿cuál
de las siguientes afirmaciones es correcta?
a.
La hipótesis que intentan probar los
investigadores aparece representada en
la H1.
b.
El estadístico de prueba se distribuye
según el modelo t de Student con 30
grados de libertad.
c.
Se concluye que los ambidiestros
escriben más rápido con una de sus
manos que con la otra.
d.
El equipo cometió un error de tipo I al
rechazar la hipótesis nula.
Un estudio publicado recientemente asegura
que el 30% de los argentinos sufre obesidad
abdominal por el sedentarismo. Asimismo,
afirma que 2 de cada 10 personas con
obesidad abdominal también presentan
diabetes, lo que aumenta considerablemente
el riesgo de la muerte. Considere una
muestra aleatoria de 6 argentinos con
obesidad abdominal, ¿cómo calcularía la
probabilidad de que más de la mitas
padezcan, además, diabetes?
a.
Como X ~ B (6; 0.2); entonces P (X ≥ 3).
b.
Como X ~ B (6; 0.2); entonces P (X ≥ 4).
c.
Como X ~ B (10; 0.3); entonces P (X > 5).
d.
Como X ~ B (6; 0.2); entonces P (X > 5).
PREGUNTA 5
En un contraste unilateral se decidió
rechazar la hipótesis nula con un valor p de
0.03.
Esto significa que…
a.
la hipótesis nula tenía baja probabilidad
de ser confirmada (p = 0.03).
b.
se obtuvo una diferencia muestral
estadísticamente significativa.
c.
los investigadores debieron adoptar un
nivel de significación del 1%.
d.
el rechazo de la hipótesis se debe a que
se cometió un error de tipo I.
PREGUNTA 6
Para que una variable se comporte según el
modelo binomial, es necesario que se
cumpla la condición de independencia.
La condición de independencia precisa que
sean independientes…
a.
la probabilidad de éxito y de fracaso de la
variable dicotómica.
b.
los parámetros n y p que caracterizan al
modelo.
c.
las n observaciones de la variable
dicotómica
d.
la variable dicotómica y la variable
binomial.
MODELO 5 – SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 7
PREGUNTA 9
Según una investigación realizada en 2002
sobre parejas divorciadas, el tiempo
promedio de duración de un matrimonio se
distribuye normalmente con una media de 12
años. Una profesional sospecha que este
valor está desactualizado. Su experiencia
como terapeuta de parejas le hace pensar
que la duración de los matrimonios es
actualmente menor. Decidió seleccionar una
muestra aleatoria de 35 parejas
recientemente divorciadas y registró una
media de 10 años de casados con un desvío
de 2 años. Los resultados le permitieron
confirmar su hipótesis para un nivel del 5%.
Los investigadores deben plantear hipótesis
estadísticas sobre…
a.
el valor del parámetro media de años de
casados que tiene la población de
parejas divorciadas en la actualidad.
b.
la diferencia entre el parámetro de la
cantidad de años de casados en 2002 y
el estadístico obtenido en la actualidad.
c.
la diferencia entre las medias de años de
casados de una muestra de 2002 y de
una muestra actual.
d.
el valor del parámetro media de años de
casados que tiene la población de
parejas en 2002.
PREGUNTA 8
La distribución muestral de la media es la
distribución de…
a.
los tamaños de muestras obtenidas en
una misma población.
b.
los valores de la variable en la población.
c.
las medias de múltiples muestras del
mismo tamaño.
d.
las observaciones de la variable en una
sola muestra.
Antes de comenzar con el estudio, los
profesionales del Hospital Gosset
necesitaron comparar los niveles de
ansiedad del “Grupo Tratamiento” y del
“Grupo Control” para verificar cierta
equivalencia inicial entre ambos grupos.
Consideraron los puntajes promedios en
Ansiedad de la muestra “Nuevo tratamiento”
(Media = 12) y de la muestra “Control”
(Media = 11). Llevaron a cabo un contraste
de hipótesis bilateral para dos medias
independientes y utilizaron un alfa de 0.05.
¿Cuál de los siguientes resultados y
conclusiones es compatible con las
expectativas de los investigadores?
a.
Obtener un estadístico t = 1.38 y p =
0.168 para concluir que la población que
recibe el Nuevo Tratamiento tiene una
media mayor a la del Control en
Ansiedad.
b.
Obtener un estadístico t = 2.09 y p =
0.037 para concluir que la diferencia de
medias en Ansiedad de ambas
poblaciones no es estadísticamente
significativa.
c.
Obtener un estadístico t = 2.09 y p =
0.037 para concluir que la población que
recibe el Nuevo Tratamiento tiene una
media mayor a la del Control en
Ansiedad.
d.
Obtener un estadístico t = 1.38 y p =
0.168 para concluir que la diferencia de
medias en Ansiedad de ambas
poblaciones no es estadísticamente
significativa.
PREGUNTA 10
Una variable se distribuye normalmente con
media μ = 20 y desviación estándar de σ = 2.
Después de agregar 3 puntos a cada valor
de la variable en la población ¿cuáles son
los nuevos valores para la media y la
desviación estándar?
a. μ = 23 y σ = 2.
b. μ = 20 y σ = 5.
c. μ = 23 y σ = 5.
d. μ = 20 y σ = 2.
MODELO 6 - SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 1
Un psicólogo está estudiando la distribución
de los Coeficientes Intelectuales (CI) para
jóvenes de 17 años de una escuela
secundaria local. El profesional midió el CI
de una muestra de 9 jóvenes de esta escuela
secundaria seleccionados al azar y obtuvo
una media de 114. Se propuso evaluar la
hipótesis de que el promedio de CI de la
población de jóvenes de 17 años es de 100
puntos contra la alternativa de que es
diferente de 100. Supone que una
distribución normal con un desvío de 15 es
un buen modelo para esta variable. Al
realizar la prueba de hipótesis registró un
estadístico de contraste de 2.8 con un valor
p = 0.005. Con un nivel de significación α =
0.01, el psicólogo debe decidir:
a. Rechazar la hipótesis nula que afirma
que la media de CI es 100.
b. Rechazar la hipótesis nula que afirma
que la media es 114.
c. No rechazar la hipótesis nula que afirma
que la media de CI es 114.
d. No rechazar la hipótesis nula que afirma
que la media de CI es 100.
PREGUNTA 2
En el modelo normal la tipificación implica
transformar:
a. las probabilidades del modelo en
puntuaciones típicas.
b. las probabilidades más elevadas en
puntajes Z.
c. los valores de la variable en las
probabilidades del modelo.
d. los valores de la variable en puntuaciones
típicas.
PREGUNTA 3
Se sabe a ciencia cierta que las poblaciones
independientes A y B tienen medias iguales.
No obstante, se realizó una prueba de
hipótesis de diferencia de medias
independientes con la que se concluyó que
la diferencia entre las medias de ambas
poblaciones es estadísticamente
significativa. En consecuencia, se cometió…
a. un error en el tipo de prueba realizado.
b. un error en las expectativas del
investigador.
c. un error de tipo I.
d. un error de tipo II.
PREGUNTA 4
Siguiendo el modelo binomial, se calculó la
probabilidad de que en una muestra aleatoria
de alumnos todos aprueben el examen y se
obtuvo 0,60. Es decir, X se distribuye B (p,
n); entonces P (X = 5) = 0,60. A partir de esta
información, seleccione la afirmación
correcta.
a. La probabilidad de que todos
desaprueben es de 0,60.
b. La probabilidad de que ninguno
desapruebe es de 0,60.
c. La probabilidad de que ninguno
desapruebe es de 0,40.
d. La probabilidad de que todos
desaprueben es de 0,40.
PREGUNTA 5
En una población determinada se incluye en
la “clase laboral activa” a todas aquellas
personas que superan los 18 años y que no
superan los 70 años. Los que han quedado
por fuera de este intervalo son incluidos en
la categoría “clase laboral pasiva”. Sabiendo
que la edad de la población se distribuye
normalmente, la probabilidad de que una
persona elegida al azar pertenezca a la clase
pasiva se calcula como:
a. P (X ≥ 18) + P (X ≤ 70).
b. P (X ≥ 70) + P (X ≤ 18).
c. P (X ≥ 70) – P (X ≤ 18).
d. P (X ≤ 18) – P (X ≥ 70).
PREGUNTA 6
La aplicación del modelo binomial depende
de dos condiciones o supuestos
denominados…
a. estabilidad e independencia.
b. éxito y fracaso.
c. p y n.
d. variable dicotómica y variable Bernoulli.
PREGUNTA 7
La relación entre dos variables será más
intensa cuando el coeficiente r de Pearson:
a. se aproxime a +1.
b. se aproxime a -1.
c. tienda a +infinito.
d. se aproxime a -1 o +1.
MODELO 6 - SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 8
Un psicólogo está realizando un estudio para
investigar si una técnica terapéutica es
eficaz para el manejo de la ansiedad en
pacientes con TAG. El psicólogo mide los
niveles de ansiedad de cada paciente antes y
después de recibir la terapia ¿Qué hipótesis
nula y alternativa debería plantear para
poder aplicar una prueba de hipótesis para
muestras relacionadas?
a. H0: No hay diferencia entre los niveles de
ansiedad antes y después de la terapia. /
H1: Hay una diferencia significativa entre
los niveles de ansiedad antes y después
de la terapia.
b. H0: Hay una diferencia significativa entre
los niveles de ansiedad antes y después
de la terapia. / H1: No hay diferencia
entre los niveles de ansiedad antes y
después de la terapia.
c. H0: Los niveles de ansiedad después de
la terapia son iguales o menores que los
niveles de ansiedad antes de la terapia. /
H1: No hay diferencia entre los niveles de
ansiedad antes y después de la terapia.
d. H0: Los niveles de ansiedad después de
la terapia son iguales o mayores que los
niveles de ansiedad antes de la terapia. /
H1: Hay diferencia en los niveles de
ansiedad antes y después de la terapia.
PREGUNTA 9
¿Cuál de las siguientes afirmaciones sobre
las hipótesis estadísticas es correcta?
a. La H0 establece que existe una diferencia
estadísticamente significativa entre los
que afirma y la evidencia empírica.
b. La H0 es una suposición que inicialmente
se acepta como verdadera y se busca
evidencia para contrastarla.
c. La H1 es una afirmación que se acepta
como verdad absoluta toda vez que
evidencia muestral permite rechazar H0.
d. La H1 es siempre una afirmación que
refleja la intención de lo que quiere
demostrar el investigador.
PREGUNTA 10
Una investigadora en teoría de género se
propone demostrar empíricamente la brecha
salarial que perjudica a las mujeres. La
investigadora se basó en información
ofrecida por un organismo gubernamental
cuyas estadísticas revelaron que el salario
mensual de la población de varones en
cargos ejecutivos de empresas privadas se
distribuye normalmente con media $1.5
millones. Sin embargo, en una muestra
aleatoria de 65 mujeres que se desempeñan
en trabajos similares se observó una media
de $1.3 millones con un desvío de $700mil. A
partir de la información recolectada se
planteó una prueba de hipótesis y se obtuvo
un estadístico de contraste de -2,29 con un p
valor de 0,013. Señale la afirmación correcta:
a. Para un alfa del 1%, la investigadora
logró demostrar empíricamente la brecha
salarial de los sueldos de varones y
mujeres.
b. El estadístico de contraste se distribuye
según el modelo t de Student con 64
grados de libertad.
c. Para demostrar la brecha salarial, la
investigadora tuvo que plantear un
contraste unilateral a la derecha.
d. Se aplicó una prueba de hipótesis para la
diferencia de dos muestras
independientes.
MODELO 7 - SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 1
En una publicación realizada por
profesionales de un hospital de Ushuaia se
informa que un cuarto de los pacientes que
recurren al servicio consulta por algún tipo
de adicción. Un psicólogo que trabaja en esa
institución seleccionó al azar un grupo de 5
pacientes y calculó la probabilidad de que
por lo menos 3 consulten usando las
siguientes expresiones. Señale la expresión
correcta:
a. como X ~ B (0.4, 5), entonces P (X < 3).
b. como X ~ B (0.25, 5), entonces P (X < 3).
c. como X ~ B (0.4, 5), entonces P (X ≥ 3).
d. como X ~ B (0.25, 5), entonces P (X ≥ 3).
PREGUNTA 2
Al mantener la H0:
a. seguro se comete un error de tipo I.
b. es probable cometer un error de tipo II.
c. seguro se comete un error de tipo II.
d. es probable cometer un error de tipo I.
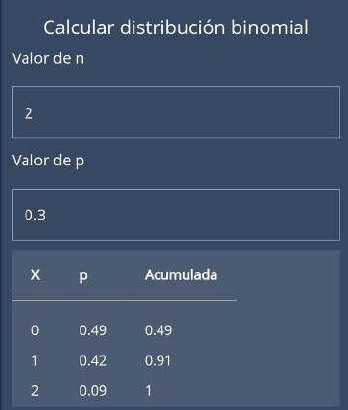
PREGUNTA 3
Considere la siguiente imagen obtenida con
la app de la cátedra y señale la afirmación
correcta:
a. el valor 2 es el que presenta menor
probabilidad.
b. la variable binomial tiene dos valores.
c. la probabilidad de que aparezca el éxito
es de 0.49.
d. es altamente probable que aparezca el
valor 1.
PREGUNTA 4
¿Cuál de las siguientes afirmaciones sobre
la distribución normal es correcta?
a. Tiene una asíntota ubicada en el eje de
las ordenadas.
b. Tiene 3 puntos de inflexión negativos y
otros 3 puntos positivos.
c. El área bajo la curva no se modifica
cuando cambian los parámetros.
d. La mitad del área bajo la curva es
negativa.
PREGUNTA 5
En una prueba de hipótesis de una media
con varianza poblacional conocida, la media
de la distribución muestral del estadístico de
contraste está vinculada con:
a. el valor del estadístico media observado
en la muestra.
b. el parámetro que se afirma en el planteo
de H0.
c. la media de la distribución de
probabilidades t de Student.
d. la regla de decisión adoptada para
contrastar la H0.
PREGUNTA 6
La variable “Motivación para el ejercicio
físico” en una población de adolescentes se
distribuye normalmente con media igual a 40
y un desvío de 5 puntos. Si se extrae al azar
un adolescente de esta población, es menos
probable que obtenga puntajes:
a. entre 55 y 60.
b. entre 45 y 50.
c. entre 25 y 30.
d. menores a 25.
MODELO 7 - SEGUNDO PARCIAL ESTADISTICA MUIÑOS
PREGUNTA 7
En un estudio se relevó la edad de inicio de
prácticas sexuales en una muestra aleatoria
de 28 adolescentes residentes en CABA. Se
halló una edad promedio de 15 años con un
desvío estándar de 0.2. Los investigadores
se preguntan si estos resultados indicarían
un descenso de la edad de inicio sexual,
dado que los últimos datos en esta
población registraban una edad promedio de
16 años. Elija la traducción estadística
correcta de la hipótesis científica, eligiéndola
dentro de las siguientes opciones:
a. H0: µ < 16 y H1: µ = 16.
b. H0: µ ≥ 15 y H1: µ < 16.
c. H0: µ ≥ 15 y H1: µ < 15.
d. H0: µ ≥ 16 y H1: µ < 16.
PREGUNTA 8
La variable “Satisfacción con la vida”
medida con el test SAT se distribuye
normalmente con media 15 y desvío 2 en la
población de adultos solteros de Buenos
Aires. Un investigador desea contrastar la
hipótesis de que las personas casadas o en
pareja perciben mayores niveles de
satisfacción. Seleccionó al azar un grupo de
45 casados, les administró el SAT y obtuvo
una media de 17 puntos. El investigador
realizó el contraste de hipótesis adecuado,
para el cual asumió que la varianza
poblacional de los casados era igual a la de
la población de solteros. Basándose en la
evidencia empírica el investigador no
rechazó la hipótesis nula.
a. Se concluye que no hay evidencia
suficiente como para suponer que la
media en Satisfacción con la vida de la
población de los casados es
significativamente mayor a 15 puntos.
b. Se aplicó una prueba de diferencia de
medias de dos poblaciones
independientes conformadas por solteros
y casados con varianzas desconocidas
pero iguales.
c. El estadístico de prueba se distribuye
según el modelo t de Student con 44
grados de libertad.
d. El investigador cometió un error de tipo I
porque la diferencia entre 15 y 17 puntos
no resulta lo suficientemente grande
como para considerarla significativa.
PREGUNTA 9
Según el Teorema Central del Límite…
a. si disminuye el tamaño de la muestra, la
distribución muestral de la media se
aproxima a la normal.
b. si aumenta el tamaño de la muestra, la
distribución muestral de la media se
aproxima a la normal.
c. si el desvío de la muestra es pequeño, la
distribución muestral de la media se
aproxima a la t de Student.
d. si el desvío de la muestra es grande, la
distribución muestral de la media se
aproxima a la t de Student.
PREGUNTA 10
Con el objetivo de incrementar el nivel de
concentración se llevaron a cabo una serie
de talleres en los que participaron 40
administrativos de una compañía
seleccionados al azar. La media obtenida en
este grupo en un test de concentración
administrado luego de los talleres se
comparó con los registros históricos
obtenidos por todos los empleados de la
empresa el año pasado. Con esta
información se realizó una prueba de
hipótesis en la que se observó el valor p de
0.025 para un estadístico de prueba de 1.75.
Con estos resultados se puede concluir que
al 5%…
a. se rechaza la H0, por lo que los talleres
no resultaron efectivos.
b. se rechaza la H0, por lo que los talleres
resultaron efectivos.
c. se mantiene la H0, por lo que los talleres
no resultaron efectivos.
d. se mantiene la H0, por lo que los talleres
resultaron efectivos.
MODELOS SEGUNDO PARCIAL 2020 ESTADISTICA MUIÑOS
PREGUNTA 1
Teniendo en cuenta la Distribución de la
media muestral, señale cuál es la
proposición INCORRECTA:
a. La Media Muestral estandarizada sigue la
Distribución Normal Unitaria con media
igual a 0.
b. Si la variable X tiene Distribución Normal
con media µ y desvío estándar σ,
entonces la media muestral tiene
Distribución Normal con el mismo desvío
estándar σ.
c. Cuando la Variable X no es normal, la
distribución de la media muestral resulta
aproximadamente normal cuando los
tamaños muestrales son grandes (n>30).
d. Si la Variable X tiene Distribución Normal
con media µ y desvío estándar σ,
entonces la media muestral tiene
Distribución Normal con la misma media
µ.
PREGUNTA 2
Suponga una variable X que se distribuye
normalmente con media µ y desvío estándar
σ. Se puede afirmar entonces que los valores
de la variable X entre µ y (µ + σ) se les asigna
la misma probabilidad que a los valores de
X:
a. entre µ y (µ - σ) solo si µ=0 y σ=1.
b. entre µ y (µ - σ).
c. entre µ y (µ - σ) solo si la curtosis es igual
a 0.
d. entre µ y (µ + 2 σ).
PREGUNTA 3
Al efectuar una prueba de diferencia de
medias para muestras independientes
ocurre un error de tipo I cuando:
a. se concluye que no hay diferencia
estadísticamente significativa entre las
medias de las poblaciones cuando, de
hecho, si las hay.
b. se decide no rechazar la hipótesis nula
dado que el valor del estadístico t de
Student es compatible con ella.
c. se analizan datos pertenecientes a
muestras que no son estrictamente
independientes entre sí.
d. se resuelve que la diferencia entre las
medias poblacionales es
estadísticamente significativa cuando, de
hecho, no lo es.
PREGUNTA 4
La hipótesis alternativa de un estudio es “El
trabajo realizado bajo presión aumenta el
número de pacientes diagnosticados con
TAG en el largo plazo, en personas
vulnerables a desarrollar esa condición”. Ud.
Diría que la hipótesis nula planteada debería
ser: “El trabajo realizado bajo presión…
a. origina menor número de pacientes
diagnosticados con TAG en el largo
plazo, en personas vulnerables a
desarrollar esa condición”.
b. está relacionado linealmente con el
número de pacientes diagnosticados con
TAG, en personas vulnerables a
desarrollar esa condición”.
c. genera mayor número de pacientes
diagnosticados con TAG en el largo
plazo, en personas vulnerables a
desarrollar esa condición”.
d. no aumenta el número de pacientes
diagnosticados con TAG en el largo
plazo, en personas vulnerables a
desarrollar esa condición”.
PREGUNTA 5
El equipo interdisciplinario de investigación
del Hospital Gosset decide administrar una
muestra de 70 pacientes un test que permite
medir la inteligencia. Según registros
anteriores del Hospital el puntaje promedio
de los pacientes en dicho test es de 46
puntos. El equipo obtiene, para los 70
pacientes, una media de 49 y una desviación
típica de 5,2 puntos. Al realizar la prueba de
hipótesis se halló un valor p = 0,045. Por lo
tanto, la información muestral recabada
brinda evidencia acerca de…
a. la existencia de un incremento
estadísticamente significativo en el
puntaje medio de inteligencia un α = 0,05.
b. la inexistencia de un incremento
estadísticamente significativo en el
puntaje medio de inteligencia un α = 0,05.
c. la existencia de un incremento
estadísticamente significativo en el
puntaje medio de inteligencia un α = 0,01.
d. la inexistencia de un incremento
estadísticamente significativo en el
puntaje medio de inteligencia un α = 0,1.
Este documento contiene más páginas...
Descargar Completo
MUIÑOS - MODELOS SEGUNDO PARCIAL - ESTADISTICA.pdf
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.