
Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 1
Práctica 9 – Parte 1
Integrales
El problema de calcular áreas y volúmenes permaneció estancado, sin progresos significativos
durante casi 2000 años. En el siglo XVII Newton y Leibniz dieron comienzo a la sistematización y
al desarrollo del cálculo diferencial e integral que permitieron enlazar, en un cuerpo de
pensamiento, la derivada y la integral y conseguir así procedimientos eficaces y manejables para
estudiar diversos fenómenos de la naturaleza. La integral, junto con la derivada, se constituyó en
una herramienta poderosa para expresar y calcular diversos conceptos de la ciencia.
El área fue el primero de toda una serie de aplicaciones y nos servirá para introducir este importante
concepto.
1. Introducción
1.1 El problema del área
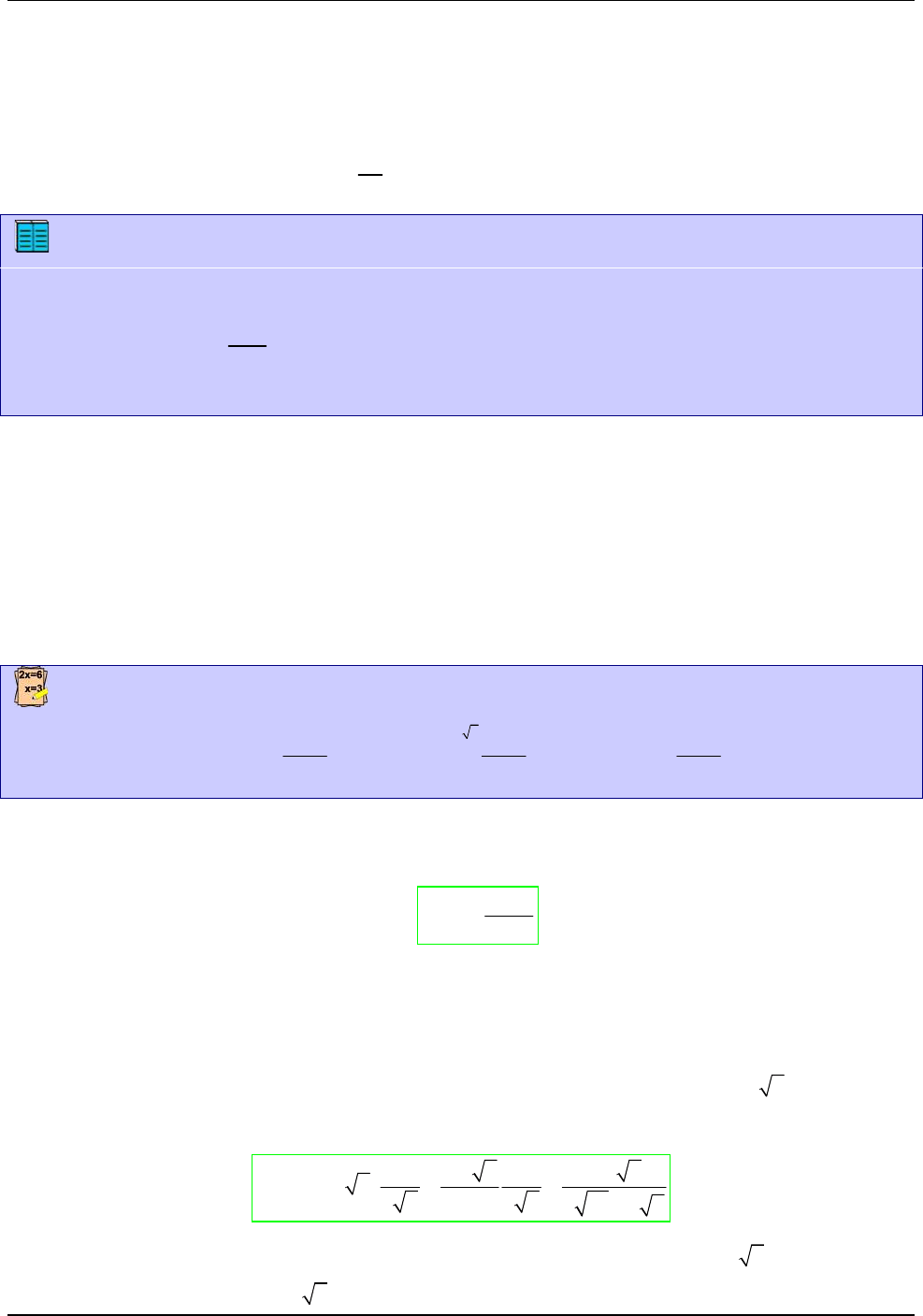
Tal como vimos en la introducción al curso este problema tiene una formulación elemental:
Dada una región como la de la figura, asociarle un número A que
represente el área de la misma en alguna unidad de medida
Este problema será sólo una motivación para definir el concepto de integral que es mucho más rico
que una herramienta para calcular áreas de regiones más o menos complicadas.
En efecto, a modo de ejemplo, consideremos la siguiente
situación:
Ejemplo: El gráfico representa la potencia, en kW
(kilovatios) que se están empleando en cada instante en
un taller con maquinaria a lo largo de un día.
Como se puede observar, la actividad comienza por las 4
de la mañana, tiene su mayor intensidad entre el
mediodía y las 18hs y a partir de allí cae hasta que a las
A
3
6
9
12
15
18
21
24
2
4
6
8
10
12
Tiempo en
horas
kW
Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 2
21hs vuelve a ser mínima (1 kW aproximadamente) que puede representar a las máquinas que
quedan funcionando durante la noche hasta la mañana siguiente. El área de la región sombreada
bajo la curva representa el consumo de energía durante todo el día.
1.2 La idea de Arquímedes
Como lo hemos hecho en varias ocasiones en este curso, resolveremos
un problema más fácil para después aplicar las ideas desarrolladas al
problema general.
Concretamente, consideraremos una función continua y positiva en el
intervalo
[ , ]a b
.
Nos proponemos definir y calcular el área comprendida entre el gráfico
de la función y el eje x
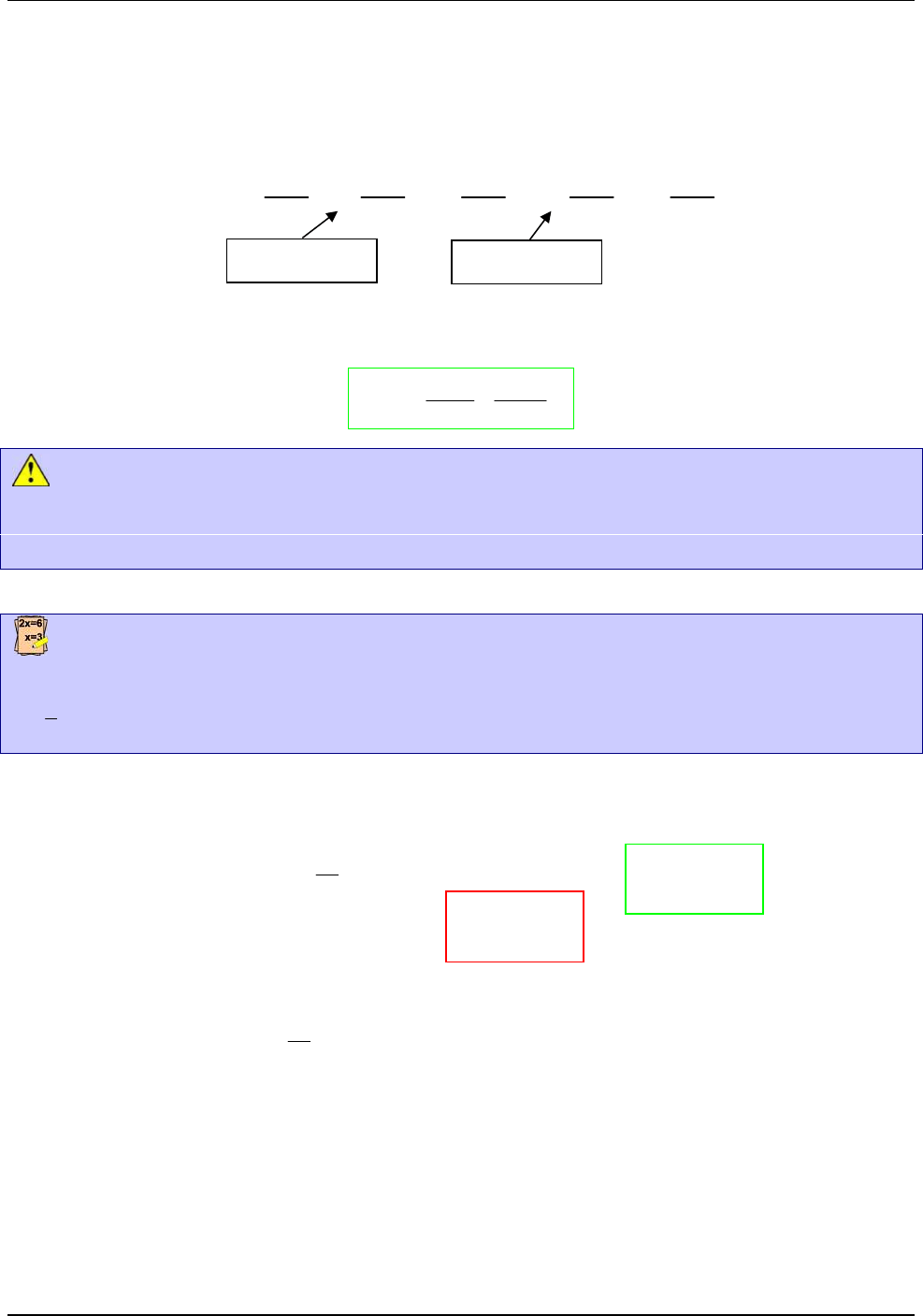
Seguiremos las mismas ideas que Arquímedes desarrolló para calcular el área del “triángulo
parabólico” hace más de 2300 años:
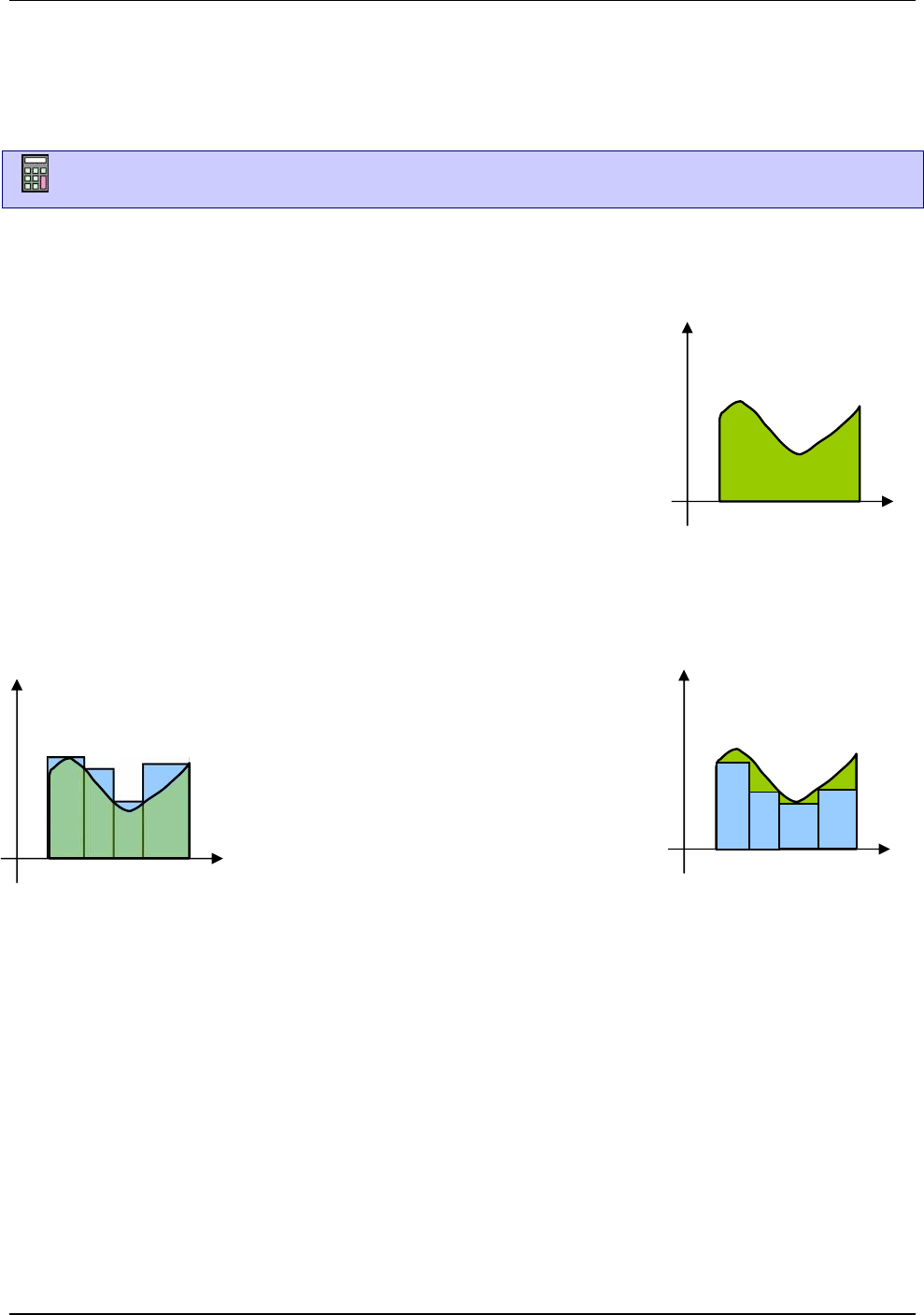
Se tapiza la región A con rectángulos. La
suma de las áreas de estos rectángulos
aproxima (por defecto) al área de la región.
También se puede aproximar el área de la
región A por exceso cubriéndola con
rectángulos y sumando sus áreas (ver figura).
La idea es tomar “la menor” de las
aproximaciones por exceso y “la mayor” de las aproximaciones por defecto y esperar que ambas
coincidan.
2. Sumas inferiores y superiores
Para formalizar esta idea es necesario introducir alguna que otra definición y la notación adecuada.
En lo que sigue la única hipótesis sobre f es que es una función acotada (
( )m f x M
) en el
intervalo
[ , ]a b
(aunque la pensaremos continua y positiva para poder seguir con la motivación de
calcular el área bajo el gráfico de f).
a
b
Aproximación por
exceso
Aproximación por
defecto
a
b
a
b
A

Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 3
Partición. Una partición P del intervalo
[ , ]a b
es un conjunto de la forma
0 1 2
: ...
n
P a x x x x b
Ejemplos
Intervalo
[0,2]
.
1
0, ,1,2
2
P
Intervalo
[0,1]
.
1 2 1
0, , ,..., ,
n
P n
n n n
Intervalo
[ , ]a b
.
, ,
2
a b
P a b
Sea
0 1
...
n
P x a x x b
una partición de
[ , ]a b
.
1
inf ( ) :
i i i
m f x x x x
,
1, 2,...i n
(el ínfimo es un mínimo si la función es continua)
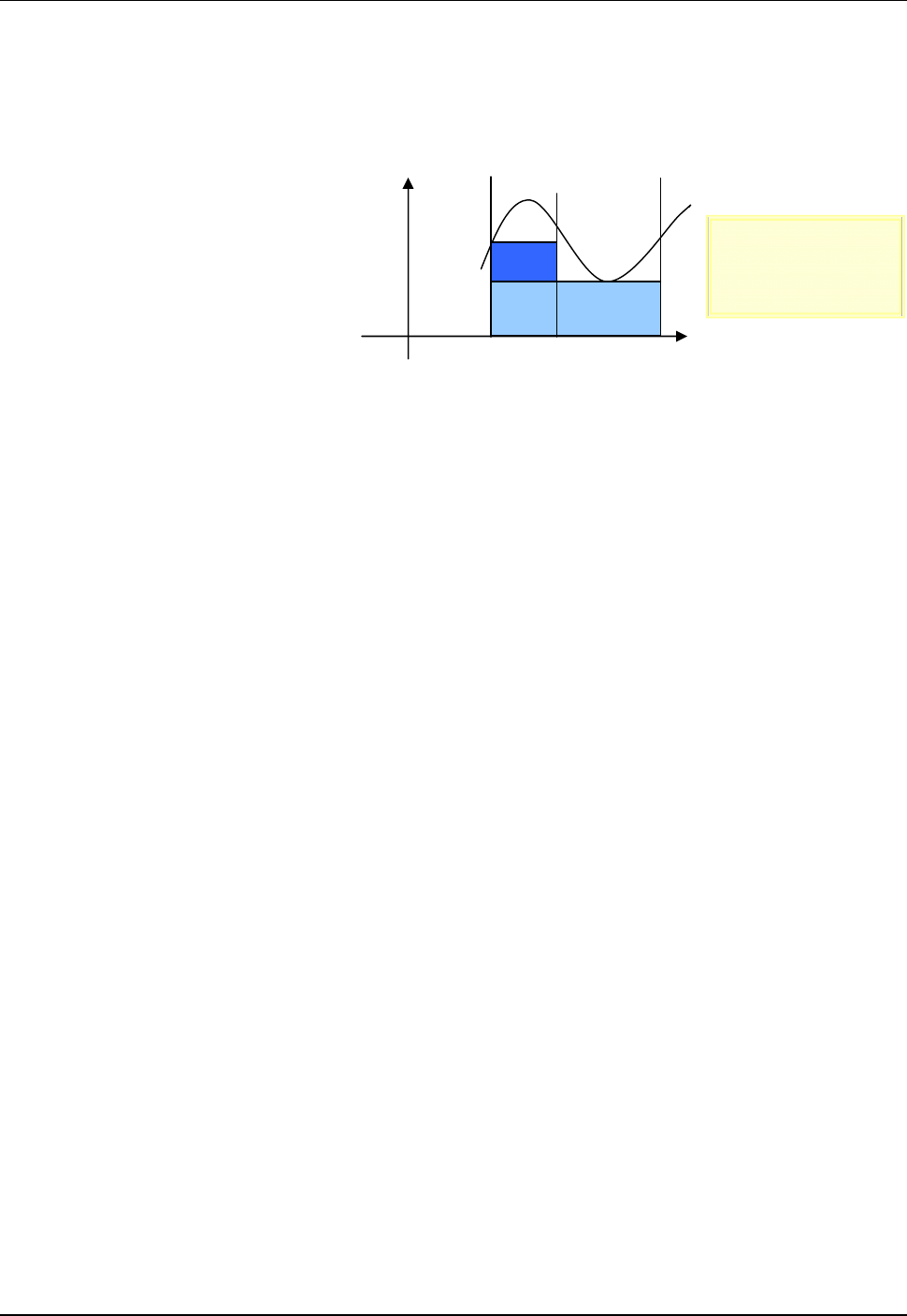
Llamamos suma inferior (de f con respecto a P) a la suma de las áreas de todos los rectángulos
azules:
1 1 0 1 1
1
( ) ( ) ... ( ) ( )
n
P n n n i i i
i
s f m x x m x x m x x
(esta suma aproxima al área de la región A por defecto)
De la misma manera si
1
sup ( ) :
i i i
M f x x x x
,
1,...,i n
se define suma superior
1
1
( ) ( )
n
P i i i
i
S f M x x
(esta suma aproxima al área de la región A por exceso).
0
1
2
1
2
0
1
para
8n
a
2
a b
b
Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 4
2.1 Propiedades de las sumas inferiores y superiores
Las siguientes observaciones llevan a la definición de integral. Todas ellas se pueden visualizar en
un gráfico por lo que no damos una
demostración formal:
1.
( ) ( )
P P
s f S f
(pues
i i
m M
)
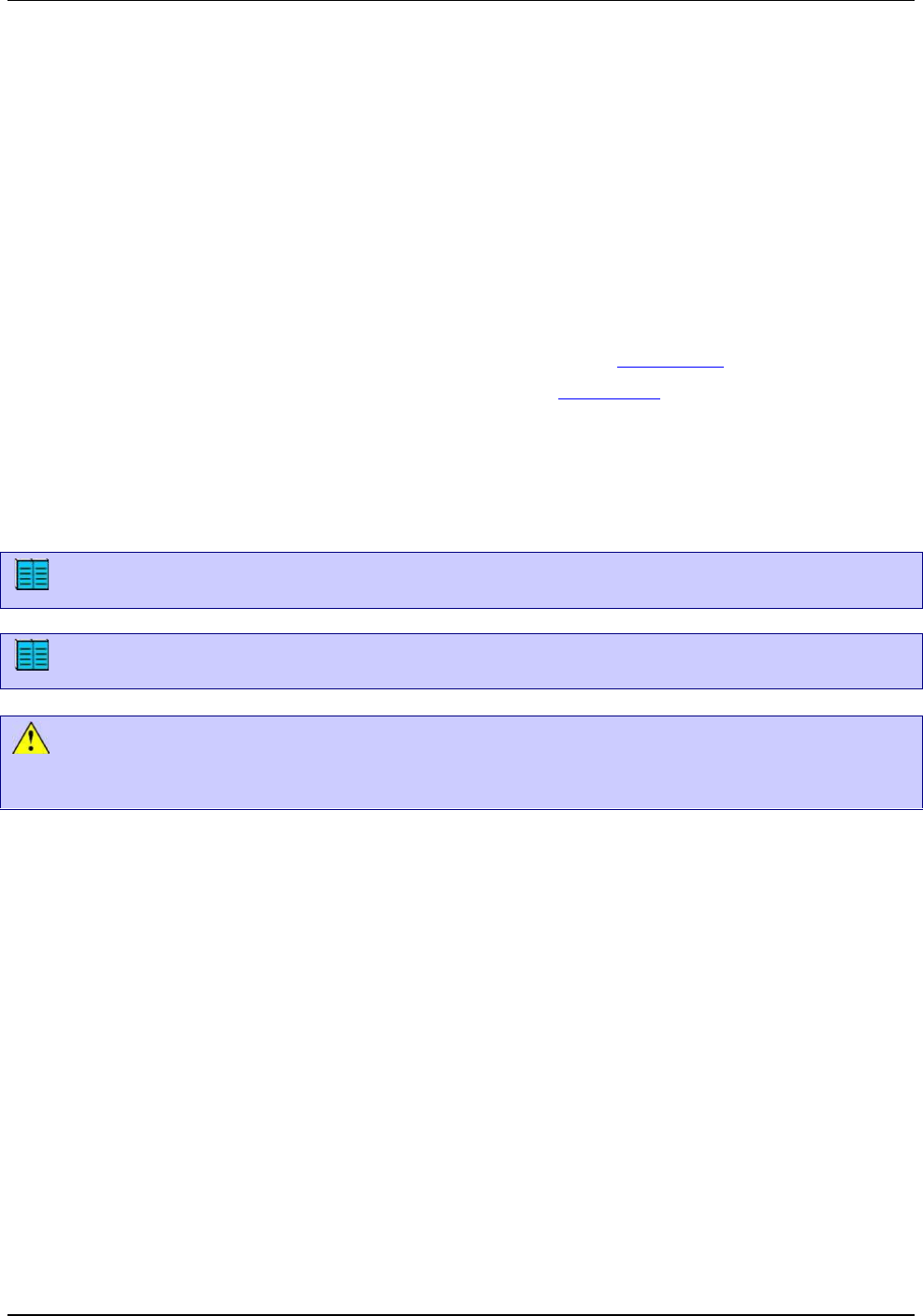
2. Si le agrego un punto a P (afino la
partición)
{ }R P c P
se tiene
( ) ( ) , ( ) ( )
P R P R
s f s f S f S f
En otras palabras, cuando afino la partición, las sumas inferiores se agrandan, las superiores se
achican.
En general si
R P
valen las desigualdades de arriba. En particular vale
( ) ( ) , ( ) ( )
P P
m b a s f S f M b a
(donde
inf ( ) : [ , ]m f x x a b
y
sup ( ) : [ , ]M f x x a b
)
3. Si P y Q son dos particiones cualesquiera del intervalo vale
( ) ( )
P Q
s f S f
Es decir todas las sumas inferiores son menores que cualquier suma superior.
Esto se deduce de las observaciones anteriores, usando que
R P Q
contiene a P y a Q, con lo
cual
( ) ( ) ( ) ( )
P P Q P Q Q
s f s f S f S f
3. La definición de integral
Podemos tomar entonces “la mayor” de las sumas inferiores y “la menor” de las sumas inferiores y
esperar que estos dos números sean los mismos: el área bajo el gráfico de f.
Lo que pasa es que, en general estos dos números no son iguales. Definimos pues la integral
inferior y la integral superior de f respectivamente:
sup ( ) :
f P
I s f P partición
inf ( ) :
f
Q
I S f Q partición
Claramente
f
f
I I
por la observación 3. Pero como dijimos antes, no siempre es igual. Cuando
son iguales decimos que la función f es integrable y ponemos
c
1i
x
i
x
Al agregar un
punto la suma
inferior se agranda
Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 5
( )
b
f
f
a
I I I f x dx
Esta notación es debida a Leibniz. El signo integral es una “deformación” del símbolo de sumatoria,
el símbolo
dx
juega el papel de la base de “rectángulos infinitamente pequeños” y
( )f x
juega el
papel de la altura de esos rectángulos. Para nosotros es un “paquete” que va junto y que resulta ser
muy adecuado para los cálculos, lo que podrá verse en las clases prácticas.
Notar que para la definición sólo se requirió la acotación de f. De hecho, si f es negativa (o toma
valores negativos) la integral es negativa o puede tomar valores negativos.
Para ver cómo funciona la definición en un ejemplo podemos ver
el Anexo A. También podremos
encontrar un ejemplo de una función que no es integrable en
el Anexo B.
3.1 Funciones integrables
Los siguientes teoremas nos dicen que la definición de integral abarca a una gran cantidad de
funciones, lo que hace al concepto útil en la práctica. No damos su demostración aquí.
Teorema: Si f es monótona entonces f es integrable.
Teorema: Si f es continua entonces f es integrable.
Es más, si f es continua en
[ , ]a b
salvo tal vez en un número finito de puntos, entonces f es
integrable.
3.2 Propiedades
Las propiedades siguientes, la integral las hereda de las sumas superiores e inferiores.
Si
,f g
son funciones integrables entonces
a)
( ( ) ( )) ( ) ( )
b b b
a a a
f x g x dx f x dx g x dx
b)
( ) ( )
b b
a a
kf x dx k f x dx
cualquiera sea
k
c)
( ) 0
a
a
f x dx

Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 6
d)
( ) ( ) ( )
b c b
a a c
f x dx f x dx f x dx
cualquiera sea
[ , ]c a b
e)
( ) ( )
a b
b a
f x dx f x dx
Usemos alguna de estas propiedades en el siguiente ejercicio
Ejercicio. Sabiendo que las funciones f y g son integrables y que
7
2
(5 ( ) 2 ( )) 23f x g x dx
y
que
7
2
(3 ( ) 2 ( )) 17f x g x dx
, calcular
7
2
( )f x dx
y
7
2
( )g x dx
Solución
Usando las propiedades a) y b) se tiene que:
Por un lado
7 7 7
2 2 2
23 (5 ( ) 2 ( )) 5 ( ) 2 ( )f x g x dx f x dx g x dx
Y por el otro lado
7 7 7
2 2 2
17 (3 ( ) 2 ( )) 3 ( ) 2 ( )f x g x dx f x dx g x dx
Nos queda un sistema de ecuaciones lineales con las dos incógnitas
7
2
( )X f x dx
e
7
2
( )Y g x dx
,
a saber
5 2 23
3 2 17
X Y
X Y
Que se resuelve fácilmente, restando una ecuación de la otra:
2 5 3 23 17 6 3X X X X
. Entonces
7
2
( ) 3X f x dx
Con lo cual
7
2
( ) 4Y g x dx
Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 7
4. Teorema fundamental del cálculo (TFC)
El uso de la definición para el cálculo de integrales resulta por lo general engorroso e
inconveniente. De todas maneras hay que destacar que los métodos numéricos rescatan y se apoyan
en la definición de integral. El ejercicio 11 de la práctica que es optativo, ilustra esta situación.
Veremos como se puede sortear el uso de la definición de integral para hallar su valor en cada caso.
En lo que sigue f es continua (y por lo tanto integrable).
Presentamos la cuestión de calcular una integral definida como un problema.
Problema: Calcular el valor de
( )
b
a
f t dt
.
Para cada
[ , ]x a b
estudiamos la “función área” definida como
( ) ( )
x
a
A x f t dt
.
Mirándola fijo se observa que:
1.
( ) ( )
b
a
A b f t dt
es el valor que buscamos.
2.
( ) 0A a
Se puede probar que
( )A x
es una función continua (para lo cual sólo se requiere que f sea
integrable). Pero vamos a calcular directamente el cociente incremental de A con vistas a calcular su
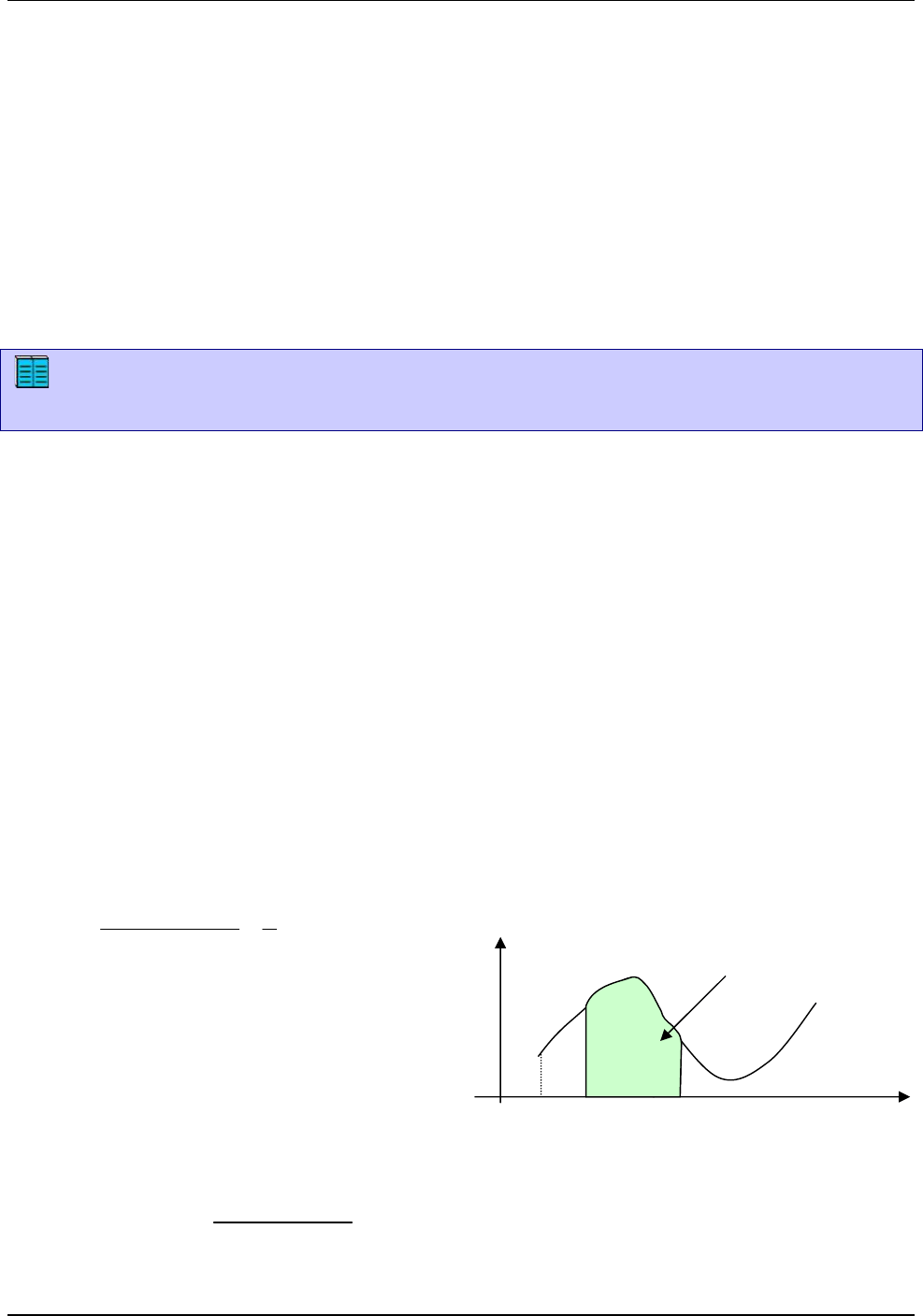
derivada. Omitiremos sutilezas en el cálculo para rescatar la idea que hay detrás de ellos.
( ) ( ) 1
( )
x h
x
A x h A x
f t dt
h h
Si ponemos
( ) min ( ) : [ , ]m h f t t x x h
y
( ) max ( ) : [ , ]M h f t t x x h
Se puede ver que (no pretende ser una demostración formal)
( ) ( )
( ) ( )
A x h A x
m h M h
h
(se ve para
0h
mirando el dibujo, para
0h
se
arregla)
x
x+h
( )
x h
x
f t dt
Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 8
0 0
lim ( ) lim ( ) ( )
h h
m h M h f x
(gracias a la continuidad de f)
Entonces se deduce que
( ) ´( ) ( )
d
A x A x f x
dx
Teorema fundamental del Cálculo. Si f es una función continua vale
( ) ( ) ( )
´
x x
a a
d
f t dt f t dt f x
dx
Este teorema constituye el resultado más importante del curso. Liga en forma muy estrecha los dos
problemas históricos del cálculo que, en términos geométricos, son: el problema del área y el
problema de hallar rectas tangentes horizontales (el Teorema de Fermat). La regla de Barrow que a
continuación enunciaremos, pone de manifiesto la potencia de este teorema y termina de resolver el
problema planteado más arriba. En adelante nos referiremos a este teorema como al TFC.
Antes de enunciar esta importante regla que será fundamental para el cálculo de integrales,
trabajemos un poco sobre cómo opera el TFC.
Ejercicio. Calcular las derivadas de las siguientes funciones:
(a)
2
0
cos
( )
1
x
t
A x dt
t
, (b)
2
0
cos
( )
1
x
t
B x dt
t
, (c)
2
2
cos
( )
1
x
x
t
C x dt
t
Solución
(a) Como la función que integramos es continua, podemos aplicar el TFC en forma directa:
2
cos
´( )
1
x
A x
x
Observemos que al derivar la integral “recuperamos” la función que se está integrando. Por eso se
suele decir que los “operadores” de derivada y de integral son uno el inverso del otro.
(b) El integrando es el mismo, pero el extremo superior tiene a una función de x. Podemos pensar a
la función B como una composición de funciones. Más precisamente
( ) ( )B x A x
siendo A la
función de la parte (a). Así pensada, podemos aplicar la regla de la cadena combinado con el TFC:
3
1 cos 1 cos
´( ) ´( )
1
2 2
2 2
x x
B x A x
x
x x
x x
En la práctica, se lo puede pensar así: reemplazo la variable de integración por
x
y lo que me da
lo multiplico por la derivada de
x
.
Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 9
Propiedad d)
Propiedad e)
El integrando
evaluado en el
extremo
superior
La derivada del
extremo
superior
evaluado en el
extremo
superior
(c) En esta función, además de tener una función de x (
2
x
) en el extremo superior, tenemos a x en el
extremo inferior. Para poder aplicar el TFC, usamos las propiedades de la integral y escribimos
( )C x
de la siguiente forma:
2 2 2
0
2 2 2 2 2
0 0 0
cos cos cos cos cos
( )
1 1 1 1 1
x x x x
x x
t t t t t
C x dt dt dt dt dt
t t t t t
Ahora estamos en condiciones de aplicar el TFC directamente en el primer término y combinado
con la regla de la cadena en el segundo:
2
2 4
cos cos
( ) 2
1 1
x x
C x x
x x
En la práctica se lo puede pensar así: La derivada de una integral es el integrando evaluado en
el extremo superior por la derivada del extremo superior, menos el integrando evaluado en el
extremo inferior por la derivada del extremo inferior.
Ejercicio. Sabiendo que la función continua f satisface
3 5
3
1
. ( ) ( 2)
x
t f t dt x x
para todo
5
3
x
, hallar
(4)f
.
Solución
Usamos el TFC para derivar la igualdad, dado que vale para todo x. Por un lado tenemos
3 5
1
(3 5) (3 5) 3. ( ) .
x
d
t f t dt
dx
x f x
Por el otro lado, usando la regla del producto
3 3 2 2
( 2) 3( 2) (4 6)
d
x x x x x x x
dx
De modo que, igualando ambas derivadas, nos queda
2
(3 5) (3 5).3 (4 6)x f x x x
El ejercicio nos pide obtener
(4)f
y esto se logra haciendo
3x
en la última igualdad:
2
(3 3 5) (3 3 5).3 3 (4 3 6)f
Hagamos las cuentas que propone el reemplazo:

Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 10
12 (4) 9 6 54f
De donde se obtiene
9
(4)
2
f
Observemos que de la igualdad
2
(3 5) (3 5).3 (4 6)x f x x x
se obtiene
2
(4 6)
(3 5)
3(3 5)
x x
f x
x
que no está definida para
5
3
x
y de allí la restricción en el enunciado del ejercicio. Haciendo
3 5t x
, podemos obtener
( )f t
pero no lo pide el problema.
4.1 Regla de Barrow
Para enunciarla adecuadamente, damos previamente la siguiente definición
Primitiva. Una primitiva de f es una función G con la propiedad
´( ) ( )G x f x
.
Por ejemplo
2
( )G x x
es una primitiva de
( ) 2f x x
.
Las primitivas de una función son “esencialmente” iguales entre sí. Más precisamente, difieren en
una constante. En efecto, si F y G son dos primitivas de f resulta
´( ) ´( ) ( )F x G x f x
. Por lo tanto
´( ) 0F G x
Por el Teorema del Valor Medio resulta
( ) ( )F x G x k
El problema que teníamos era el de calcular el valor de
( ) ( )
b
a
A b f t dt
El TFC permite calcular tal valor conociendo una primitiva de f.
En efecto, sea G una primitiva de f. Se tiene que
( ) ( ) ´ ( ) ( ) 0G x A x f x f x
, entonces
( ) ( )G x A x k
.
En particular
( ) ( ) ( )k G a A a G a
. Luego
( ) ( ) ( )
b
a
f t dt G b G a
Regla de Barrow
En otras palabras basta conocer una primitiva de f para calcular la integral.

Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 11
Ejemplo. Calcular
1
0
xdx
.
La función
2
( )
2
x
G x
es una primitiva de
( )f x x
. Usando la Regla de Barrow se obtiene
1
0
1
(1) (0)
2
xdx G G
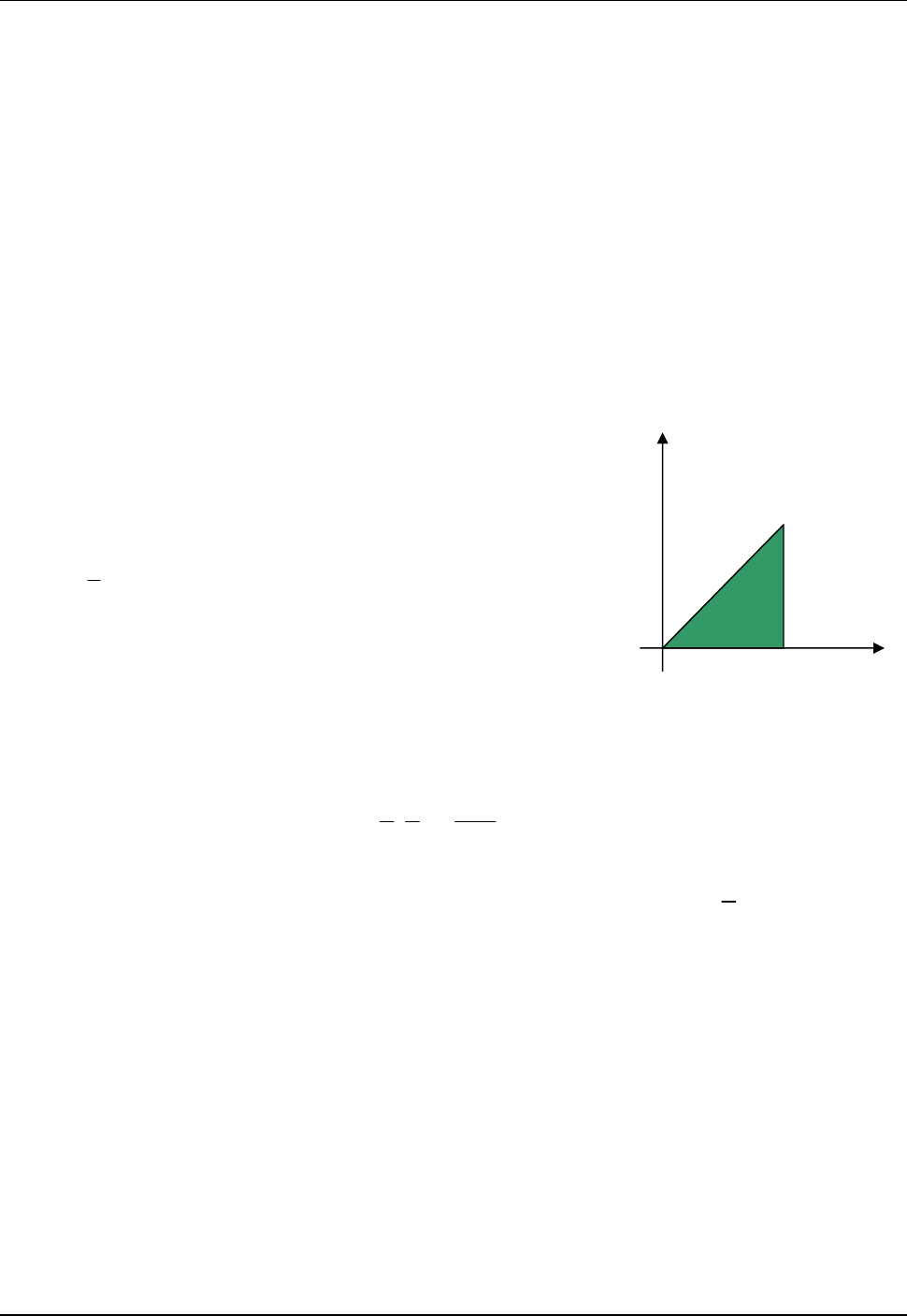
Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 12
ANEXO
A. Uso de la definición
La definición de integral es un concepto muy rico desde el punto de vista teórico y también desde el
punto de vista práctico ya que los métodos numéricos utilizados para cálculos complicados, usan
esta definición para su fundamentación. Sin embargo tiene el inconveniente que aún en los ejemplos
más sencillos, implica muchos cálculos que no siempre se pueden realizar. Damos un ejemplo aquí
para mostrar estas dificultades, que sigue básicamente las ideas que Arquímedes esbozó 300 años
antes de nuestra era y que recién Riemann pudo darle forma en el siglo XIX.
Vamos a usar la definición de integral que acabamos de dar para
calcular el área bajo el gráfico de
( ) , [0,1]f x x x
. Es decir que
calcularemos el área de un triángulo de base 1 y altura 1. Es obvio
que no necesitamos el concepto de integral para saber que el área es
igual a
1
2
, pero el cálculo nos ilustrará sobre las dificultades
prácticas que tiene la definición.
Uno de los problemas de la definición es el de considerar todas las particiones. Veremos, que, tal
como lo hizo Arquímedes, se puede trabajar con una familia de particiones, en lugar de tener que
considerar todas las particiones. Sean
1 2 1
0, , ,..., ,1
n
n
P
n n n
,
n
Son las particiones que dividen el intervalo en n partes iguales. Resulta ser
i
i
x
n
Para calcular las sumas inferiores y las sumas superiores,
( )
n
p
s f
y
( )
n
P
S f
respectivamente, como f
es creciente y gracias a que cada partición es equiespaciada, se tiene que
1
1
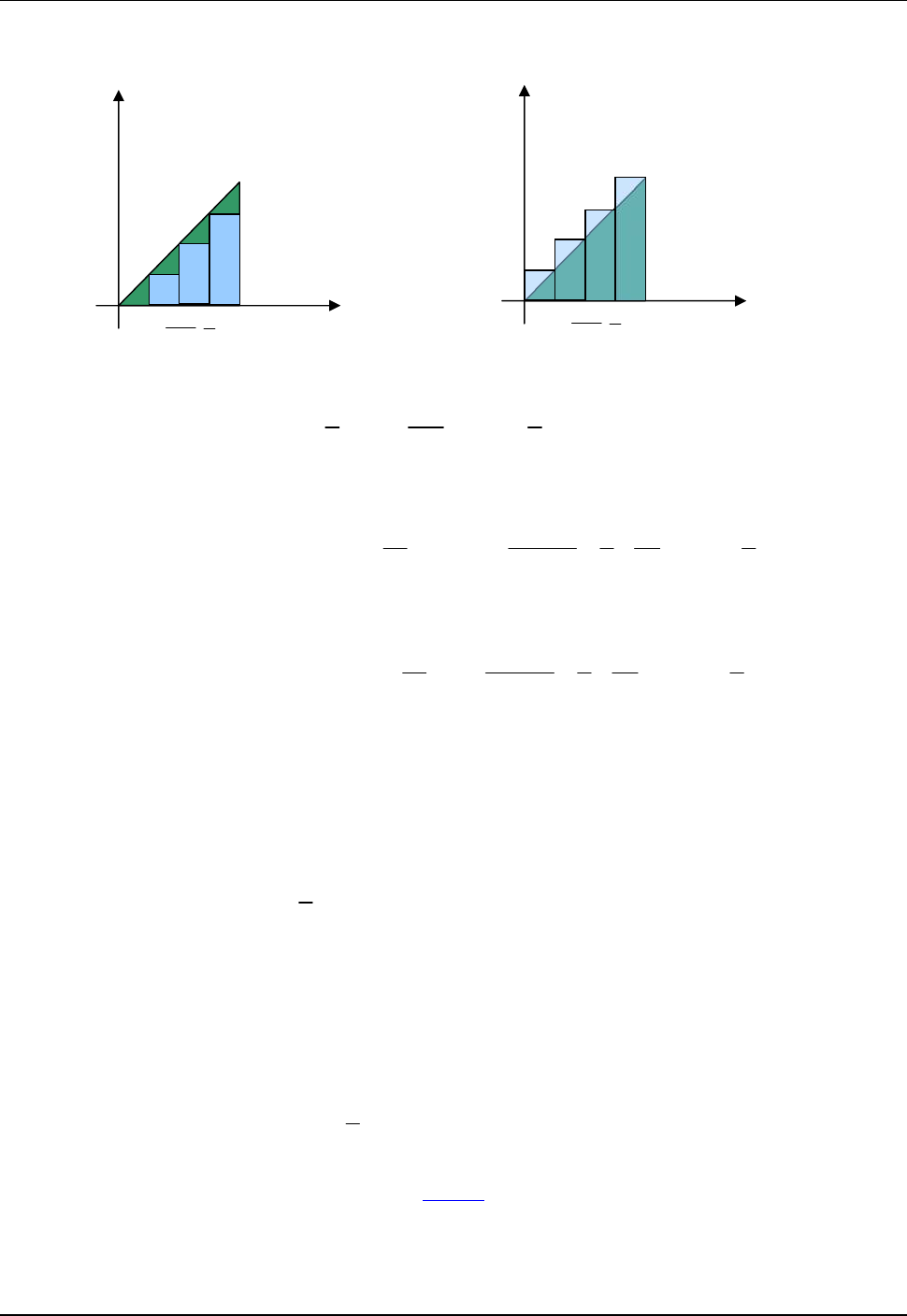
Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 13
1
1
i i
x x
n
,
1
,
i
i
m
n
, 1,2,....,
i
i
M i n
n
.
Entonces
1
2 2
1 1
1 ( 1) 1 1 1
( ) ( ) ( 1)
2 2 2 2
n
n n
crece
p i i i
n
i i
n n
s f m x x i
n n n
De la misma forma
1
2 2
1 1
1 ( 1) 1 1 1
( ) ( )
2 2 2 2
n
n n
decrece
P i i i
n
i i
n n
S f M x x i
n n n
Vemos que
( )
n
p
s f
es una sucesión creciente de números reales y que
( )
n
P
S f
es una sucesión decreciente de números reales.
1
lim ( ) lim ( )
2
n n
P P
n n
s f S f
Entonces vale que:
sup ( ) : sup ( ) : lim ( ) lim ( )
n n n
f P P P P
n n
I s f P partición s f n s f S f
inf ( ) : inf ( ) :
n
f
P Q
S f n S f Q partiición I
Luego f es integrable y vale
1
0
1
2
xdx
Volver
1
1
1i
n
i
n
1
1
1i
n
i
n

Teóricas de Análisis Matemático (28) – Práctica 9 – Integrales
Área de Matemática – Ciclo Básico Común – Universidad de Buenos Aires 14
B. Una función no integrable
La función de Dirichlet en el intervalo [0,1] es un ejemplo de función no integrable:
1
( )
0
si x
f x
si x
Por la densidad, en todo intervalo de una partición cualquiera, se tiene que
0 , 1
i i
m M
,
entonces
0 , 1
f
f
I I
.
Volver
Cintia Buxton, Lisi D’Alfonso, Flora Gutierrez, Gabriela Jeronimo, Gustavo Massaccesi, Juan Carlos Pedraza
y Juan Sabia (2015), Integrales, Teóricas de Análisis Matemático (28).

Metodos Integracion.pdf
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.