Volver a Matemática 51
8/9/22, 14:48
Funciones homográficas
www.recorridos.mate.cbc.uba.ar/mod/wiki/prettyview.php?pageid=86
1/6
Funciones homográficas
Las funciones homográficas son aquellas de la forma
con , y .
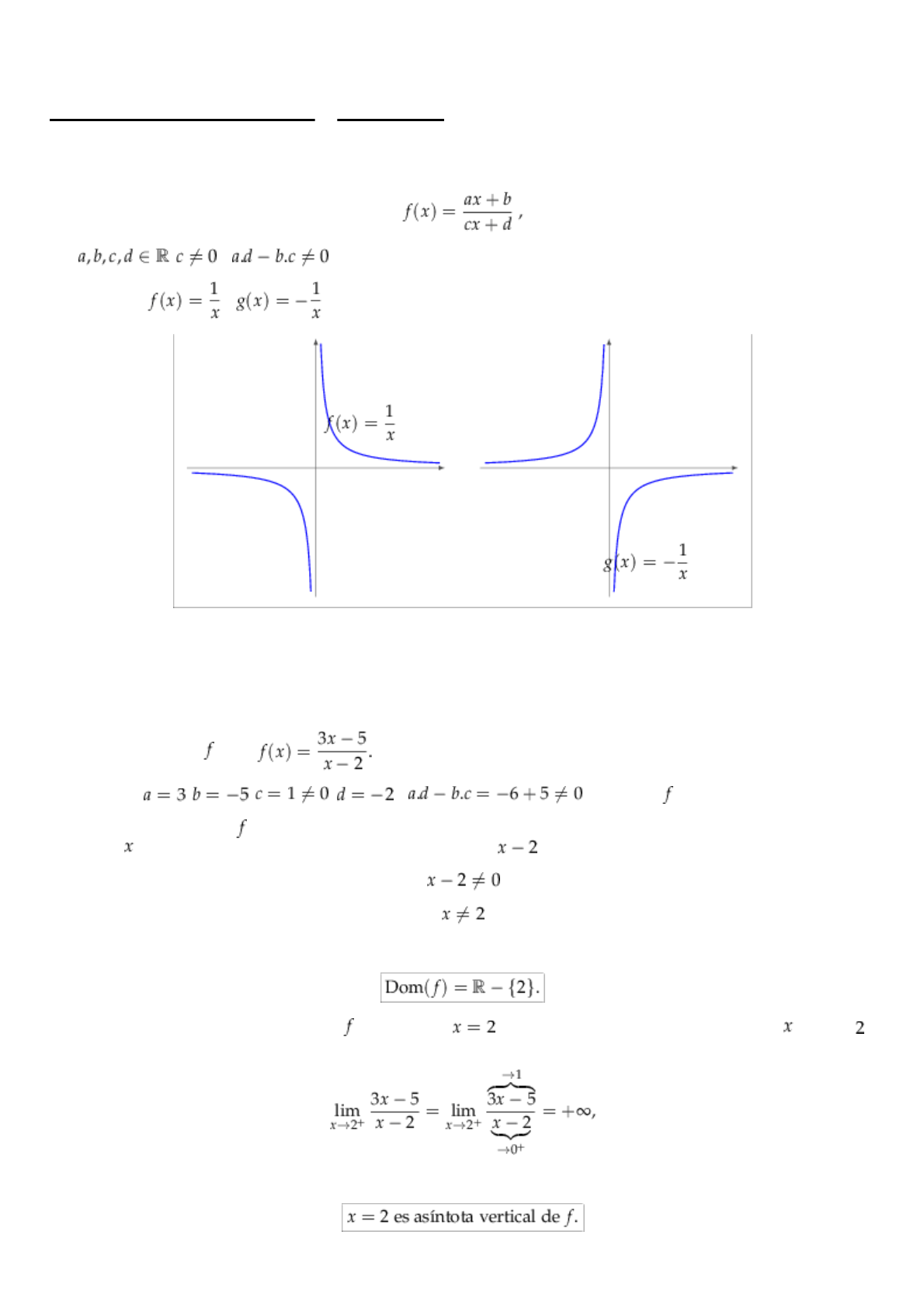
Las funciones
y , son las funciones homográficas más "básicas". Sus gráficos son:
El gráfico de cualquier función homográfica es esencialmente como el de alguna de estas dos funciones. Una de las
mayores diferencias se encuentra en la posición de las asíntotas vertical y horizontal.
Estudiemos el comportamiento de las funciones homográficas con un ejemplo.
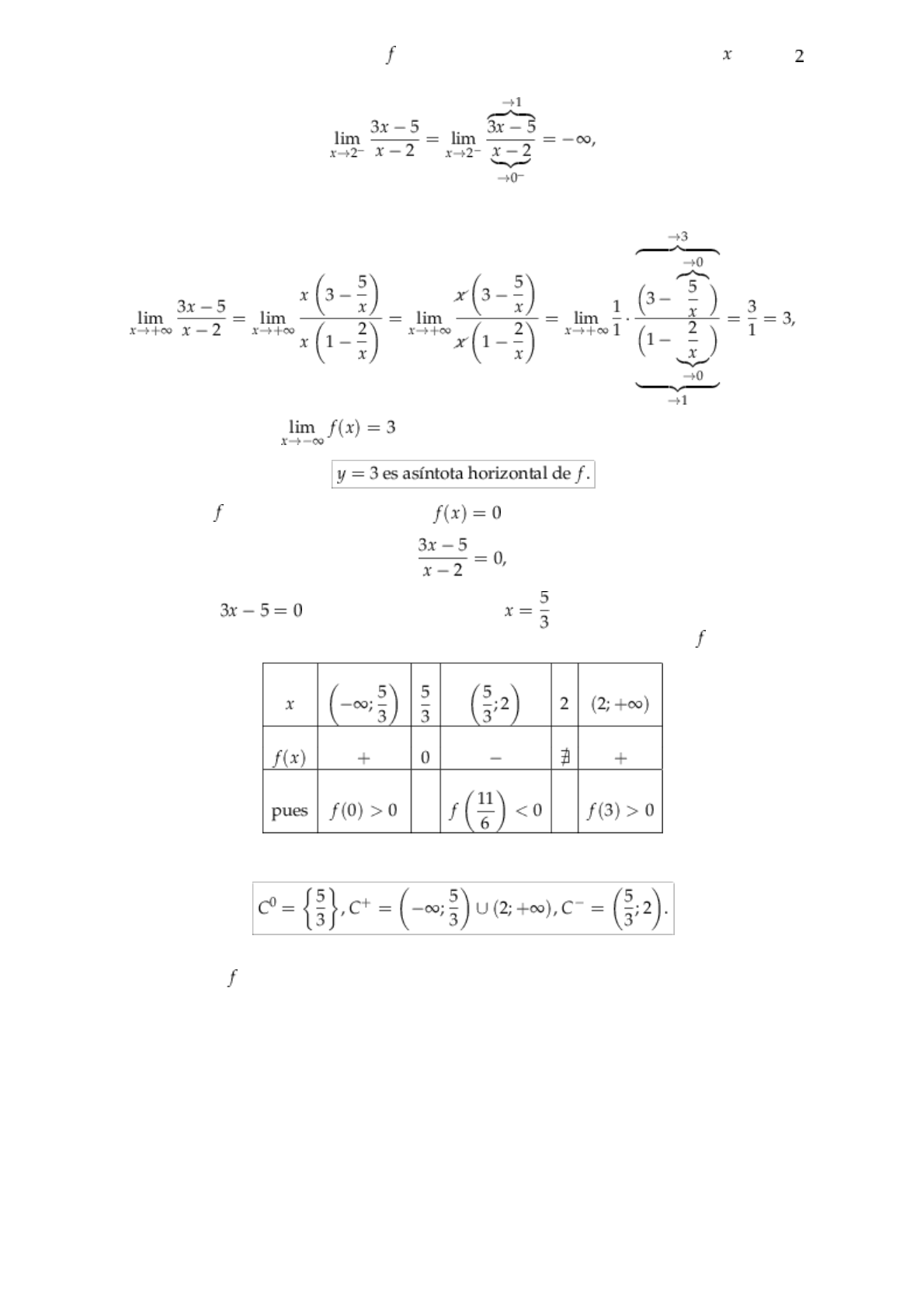
Ejemplo 1. Hallar dominio, ecuaciones de las asíntotas, ceros y conjuntos de positividad y de negatividad, y hacer un
gráfico aproximado de , para
Notemos que , , , y , por lo que es una función homográfica.
Para calcular el dominio de
, recordemos que no podemos dividir por cero, por lo que tenemos excluir del dominio los
valores de
que hagan cero el denominador, que en este caso es :
Por lo tanto
El único candidato para asíntota vertical de es, entonces, . Calculamos el límite, por ejemplo cuando tiende a
por derecha:
y como da infinito, podemos afirmar que
8/9/22, 14:48
Funciones homográficas
www.recorridos.mate.cbc.uba.ar/mod/wiki/prettyview.php?pageid=86
2/6
Como vamos a realizar un gráfico aproximado de , nos conviene estudiar también el límite cuando tiende a por
izquierda:
Por otro lado,
y de la misma manera obtenemos , por lo que
Para hallar los ceros de debemos resolver la ecuación , es decir
y esto sucede si y solo si , o equivalentemente, cuando . Como es una función continua en su dominio,
podemos estudiar su positividad y negatividad aplicando el Corolario del Teorema de Bolzano a en su dominio:
De aquí deducimos:
Un gráfico aproximado de
es
8/9/22, 14:48
Funciones homográficas
www.recorridos.mate.cbc.uba.ar/mod/wiki/prettyview.php?pageid=86
3/6
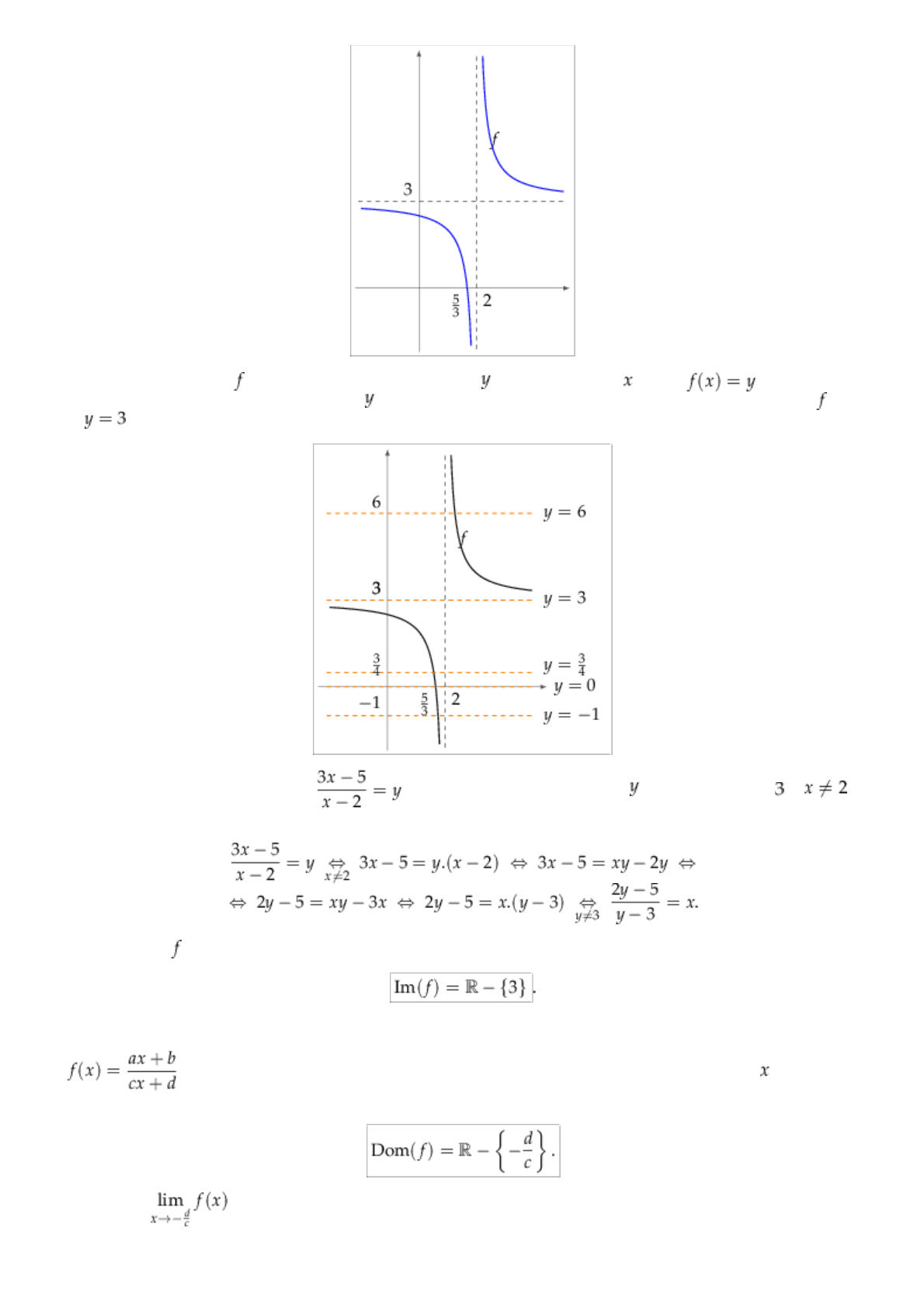
Para calcular la imagen de , debemos ver para qué valores de podemos hallar un tal que . Notemos que si
graficamos una recta horizontal por el valor de
que estamos considerando, estas rectas intersecan el gráfico de salvo
para
, que es la asíntota horizontal.
Analíticamente, vemos que la ecuación se puede resolver para cualquier que sea distinto de (y
porque, recordemos, no se puede dividir por cero):
Así, la imagen de es
En general:
Si
es una función homográfica, su dominio se encuentra excluyendo aquellos valores de que hacen
cero el denominador:
Como el límite da infinito,
8/9/22, 14:48
Funciones homográficas
www.recorridos.mate.cbc.uba.ar/mod/wiki/prettyview.php?pageid=86
4/6
Para hallar la ecuación de la asíntota horizontal, hay que calcular el siguiente límite
de la misma manera obtenemos . Por lo tanto
y su imagen es
Otra forma de expresar una función homográfica
Así como las funciones cuadráticas se pueden expresar de tres maneras distintas (forma polinómica, forma canónica y
forma factorizada), las funciones homográficas también se pueden expresar de la siguiente manera:
con y .
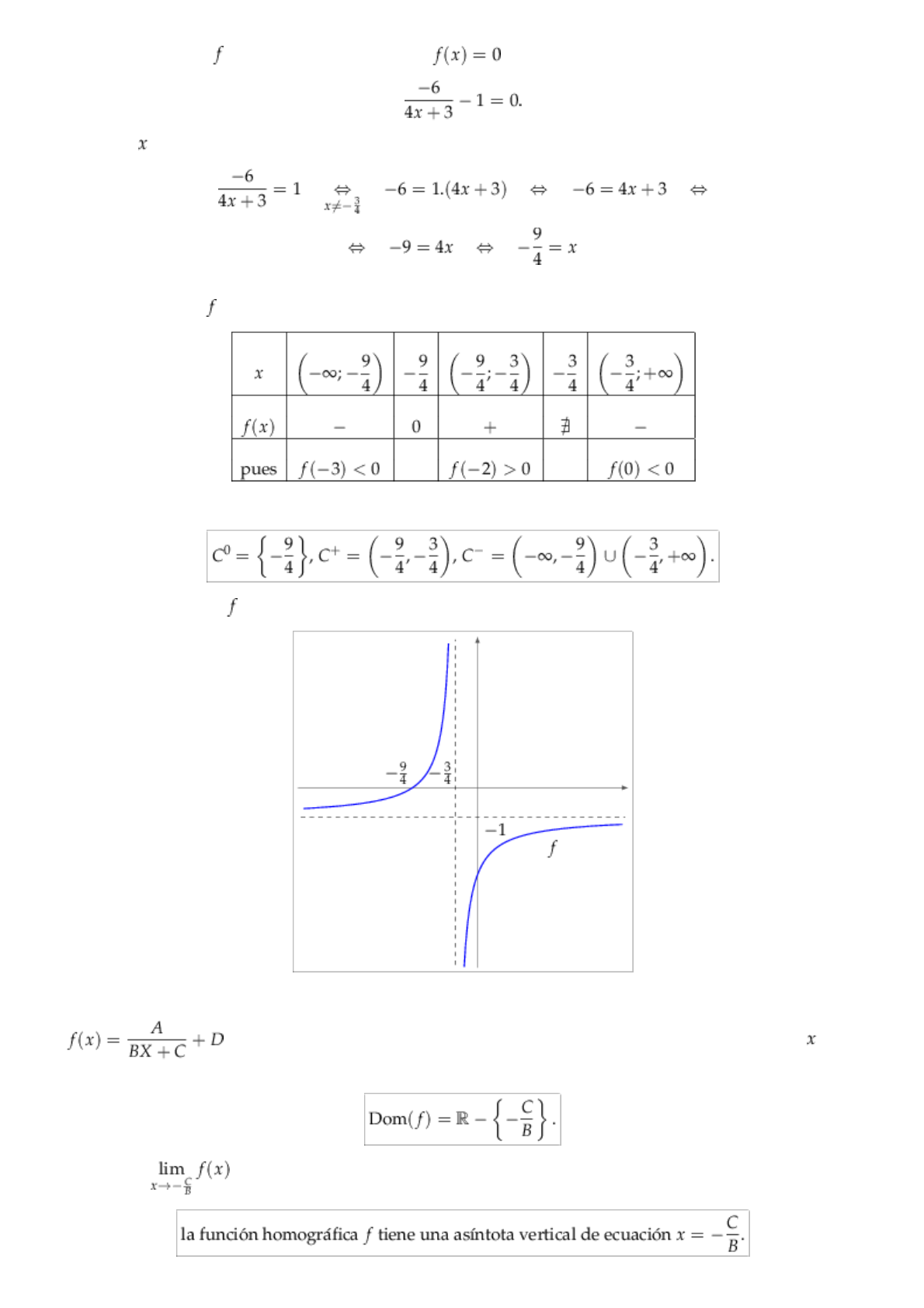
Ejemplo 2. Hallar dominio, ecuaciones de las asíntotas, ceros y conjuntos de positividad y de negatividad, y hacer un
gráfico aproximado de , para
donde , , y .
Para calcular el dominio de
, recordemos que no podemos dividir por cero, por lo que tenemos excluir del dominio los
valores de
que hagan cero el denominador. En este caso, el denominador, es cero si y solo si , por lo
que
El único candidato para asíntota vertical de es, entonces, . Si calculamos el límite, por ejemplo cuando tiende
a
por derecha, nos da , por lo que podemos afirmar que es asíntota vertical de .
Además,
En este caso, el cálculo del límite cuando
tiende a infinito es más fácil que en el caso anterior:
y por lo tanto tiene una asíntota horizontal de ecuación . Su imagen es, entonces,
8/9/22, 14:48
Funciones homográficas
www.recorridos.mate.cbc.uba.ar/mod/wiki/prettyview.php?pageid=86
5/6
Para hallar los ceros de debemos resolver la ecuación , es decir
Despejemos :
Como es una función continua en su dominio, podemos estudiar su positividad y negatividad aplicando el corolario del
Teorema de Bolzano a
en su dominio:
De aquí deducimos:
Un gráfico aproximado de es
En general:
Si
es una función homográfica, su dominio se encuentra excluyendo aquellos valores de que
hacen cero el denominador:
Como el límite da infinito, obtenemos que
8/9/22, 14:48
Funciones homográficas
www.recorridos.mate.cbc.uba.ar/mod/wiki/prettyview.php?pageid=86
6/6
Para hallar la ecuación de la asíntota horizontal, hay que calcular el siguiente límite:
de la misma manera obtenemos . Por lo tanto
y su imagen es
Notemos que es sencillo pasar de la forma a la forma , sacando denominador
común. En el Ejemplo 2, sería:
(Notar que el dominio, las asíntotas y la imagen dan lo mismo porque es la misma función.)
Funciones homográficas.pdf
browser_emoji Estamos procesando este archivo...
browser_emoji Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
. . . . .