1
CÓNICAS
CURVAS CONICAS
DEFINICIÓN: Lugar geométrico de un conjunto de puntos tales que la distancia de cada punto del
conjunto a un cierto punto fijo llamado
foco
esta en relación constante con su distancia a una
recta fija llamada
directriz
.
Todas las curvas cónicas nacen del doble cono generado por una recta (generatriz) alrededor de
un eje, describiendo una circunferencia (directriz) y manteniéndose siempre pasante por un punto
del eje (vértice del cono).
Utilizando planos de corte se obtiene distintas curvas cónicas: elipse, parábola, hipérbola,
circunferencia (caso especial de la elipse).
Excentricidad:
La excentricidad de una cónica es la relación entre las distancias de un punto P al foco y de P a la
directriz.
Parábola:
e = 1
Elipse:
1 > e > 0 (cuanto mas próxima esta la e a 0, mas redondeada es la elipse)
Circunferencia:
e = 0
Hipérbola:
e > 1 (cuanto menor sea la e, mas cerradas serán las dos ramas de la hipérbola)
2
PARÁBOLA
Es el conjunto de puntos del plano que equidistan de un punto (foco) y de una recta (directriz).
La parábola tendrá sus ramas en el eje que no esta al cuadrado.
Las coordenadas de vértice son: (h
;
k).
P es la distancia del foco a la directriz.
Parábola desplazada:
Existen dos tipos:
1) Si el eje de simetría es paralelo al eje X
Si p es + la parábola es C.
Si p es – la parábola es D.
Excentricidad de la parábola ➔ e=1
y
2
= 2p x
Ecuación de la Parábola
2) Si el eje de simetría es paralelo al eje Y
Si p es + la parábola es U
Si p es – la parábola es ∩
3
Ejemplo de aplicación al diseño:
Los espejos parabólicos de los telescopios y antenas parabólicas de radar tienen la siguiente
propiedad reflectora: los rayos emitidos desde el fofo se reflejan paralelos al eje y los rayos que
llegan al reflector paralelos al eje se reflejan pasando por el foco.
Elipse
Lugar geométrico del conjunto de todos los puntos del plano tales que la suma de las distancias a
dos puntos fijos a dos puntos fijos llamados focos es constante.
C es la distancia entre el foco y el centro.
Los dos focos están ubicados en el diámetro
mayor.
a= semieje mayor
b= semieje menor
Esta curva es simétrica respecto de ambos
ejes.
Excentricidad:
e = c
a 1 > e > 0
Elipse desplazada
a>b ➔ los focos están en el eje X
a<b ➔ los focos están en el eje Y
F
x
2
+ y
2
= 1
a
2
b
2
4
El centro de la elipse son las coordenadas (h;k) siendo h en x y k en y.
(x - h)
2
+ (y - k)
2
= 1 centro (h;k)
a
2
b
2
Elipse horizontal
a > b
Ecuación de los focos: c
2
= a
2
– b
2
Coordenadas de los focos: f
1
= (h – c ; k) f
2
= (h + c ; k)
Elipse vertical
a < b
Ecuación de los focos: c
2
= b
2
– a
2
Coordenada de los focos: f
1
= (h ; k - c) f
2
= (h; k + c)
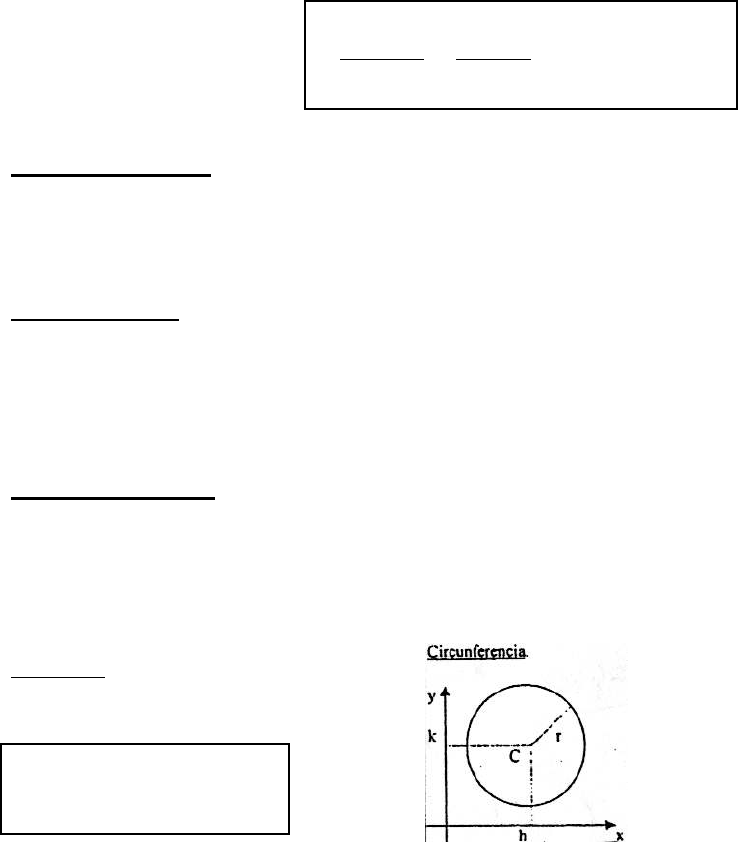
Circunferencia
Es un caso especial de la elipse donde a = b y su excentricidad es 0.
Ecuación
(x - h)
2
– (y - k)
2
= r
2
5
Hipérbola
Lugar geométrico de todos los puntos del plano tales que la diferencia de las distancias a dos
puntos fijos llamado focos es constante.
La curva es simétrica respecto de ambos ejes y no
toca al eje que esta restando.
El centro de la hipérbola son las coordenadas
(h ; k) siendo h en x y k en y.
C es la distancia entre el foco y el centro.
a es la coordenada en x del vértice y b la
coordenada en y.
Asíntotas:
c
2
= a
2
+ b
2
Puede ser de dos tipos:
Hipérbola que corta el eje x
Ecuación
(x - h)
2
- (y - k)
2
= 1
a
2
b
2
Ecuación de los vértices:
v
1
= (h – a ; k) v
2
= (h + a ; k)
Coordenadas de los focos:
f
1
= (h – c ; k) f
2
= (h + c ; k)
Excentricidad: e > 1
e = c
a
y = - b . x y = b . x
a a
X
2
- Y
2
= 1
a
2
b
2
6
Hipérbola que corta el eje y
Ecuación
(y - k)
2
- (x - h)
2
= 1
b
2
a
2
Ecuación de los vértices:
v
1
= (h ; k - b) v
2
= (h ; k + b)
Coordenadas de los focos:
f
1
= (h; k - c) f
2
= (h ; k + c)
Excentricidad: e > 1
e = c
b
EJEMPLO de APLICACIÓN AL DISEÑO
Los espejos hiperbólicos gozan de una propiedad reflectora: todo rayo de luz pasante por un foco
del espejo hiperbólico emerge pasando por el otro foco. Esta propiedad ha sido usada en la
construcción de telescopios reflectores.
FINAL simetria y grafos.doc
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.