ESTÁTICA
FÍSICA I 1H10 2025
Lic. y Farm. Vivian Coggiola
ESTÁTICA
✓ La estática es la parte de la mecánica que se ocupa de los cuerpos
sometidos a
fuerzas equilibradas, es decir, cuerpos que están en reposo o
en movimiento rectilíneo y uniforme.
✓ Todos los cuerpos se deforman cuando están sometidos a cargas. Sin
embargo, cuando se aplican en estática del sólido rígido las condiciones de
equilibrio, se supone que el cuerpo permanece rígido y no se deforma.
✓ En esta unidad se desarrollarán las ecuaciones de equilibrio para un sólido
rígido, se analizarán los diagramas de cuerpo libre y se mostrará cómo
resolver problemas de equilibrio de sólidos rígidos
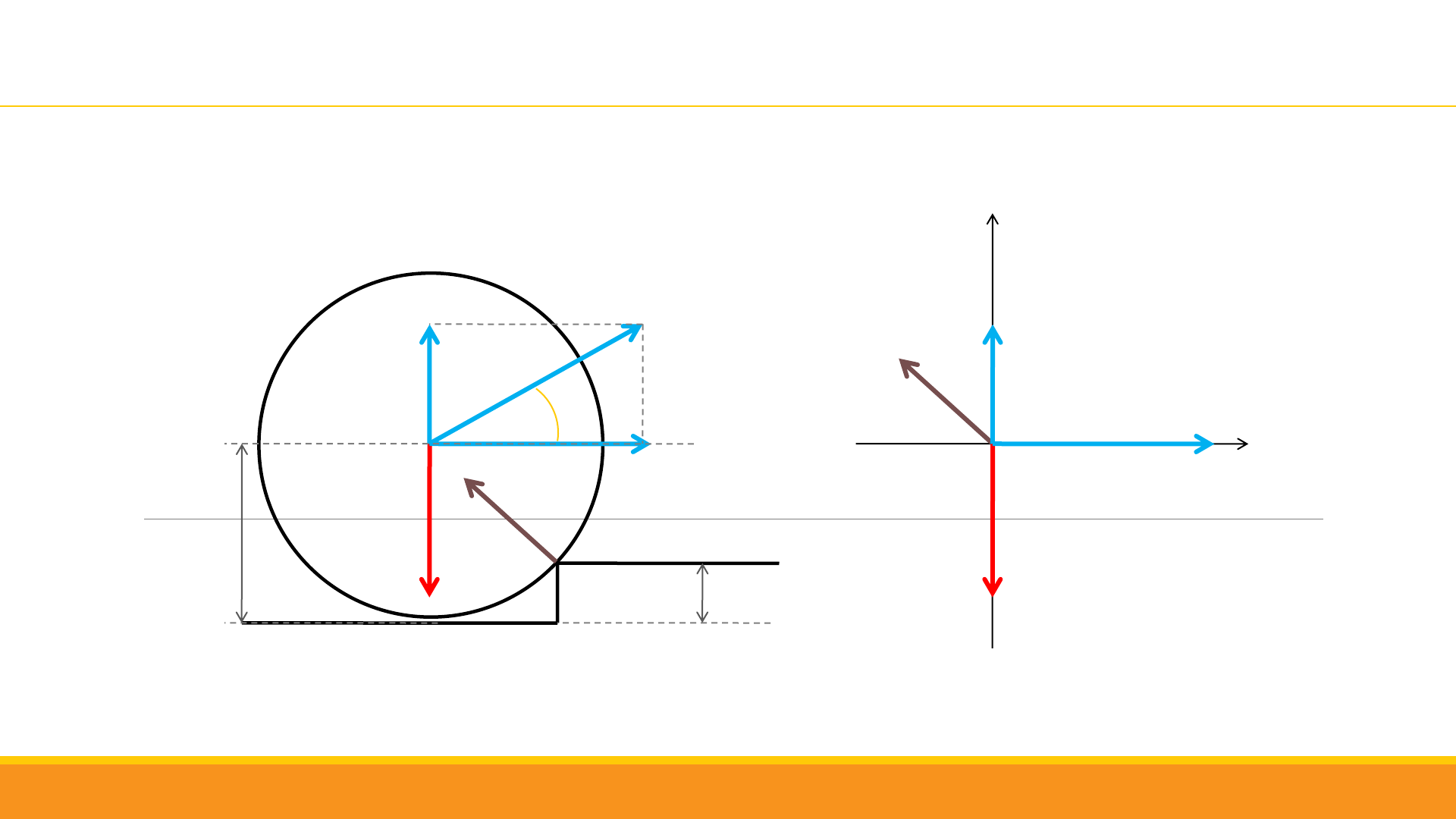
Se aplica sobre el eje de una rueda que pesa 100 N, una fuerza F que forma un ángulo de 30° con la horizontal, con el objeto
que la rueda pueda subir un escalón de 10 cm de alto, el radio de la rueda es de 30 cm. Calcular el valor mínimo de la
fuerza.
F
P
P
N
y
x
A
0,1 m
R = 0,3 m
F
y
F
x
F
y
F
x
N
30°
FÍSICA I LIC. Y FARM. VIVIAN COGGIOLA
3
Ejemplo 1. Problema 6 guía educo
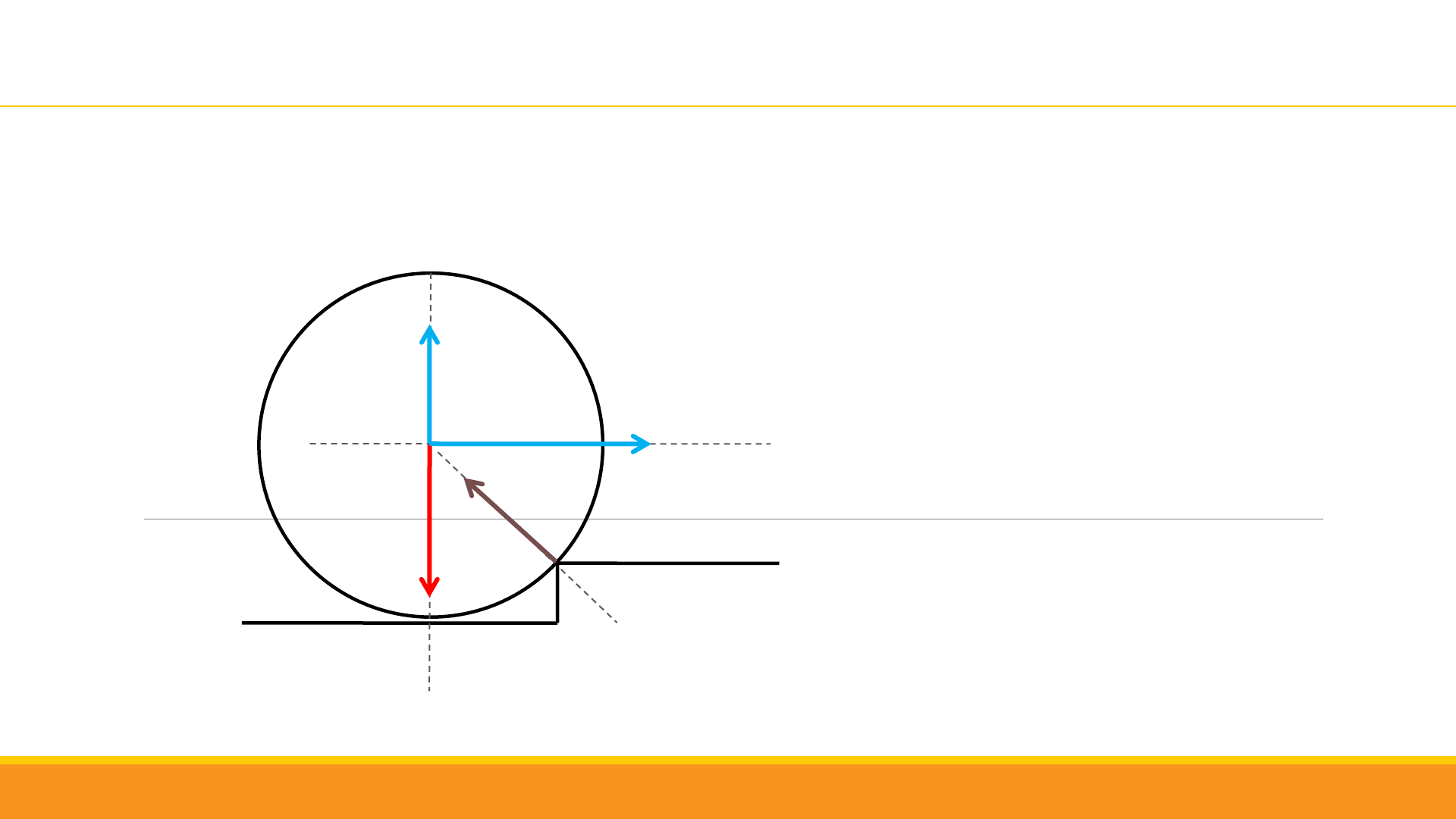
P N
A
Condición de equilibrio estático:
Tomamos momento de torsión en
el punto A:
= 0
+
= 0
+
= 0
F
y
F
x
FÍSICA I LIC. Y FARM. VIVIAN COGGIOLA
4
Se aplica sobre el eje de una rueda que pesa 100 N, una fuerza F que forma un ángulo de 30° con la horizontal, con el objeto
que la rueda pueda subir un escalón de 10 cm de alto, el radio de la rueda es de 30 cm. Calcular el valor mínimo de la
fuerza.
Ejemplo 1. Problema 6 guía educo
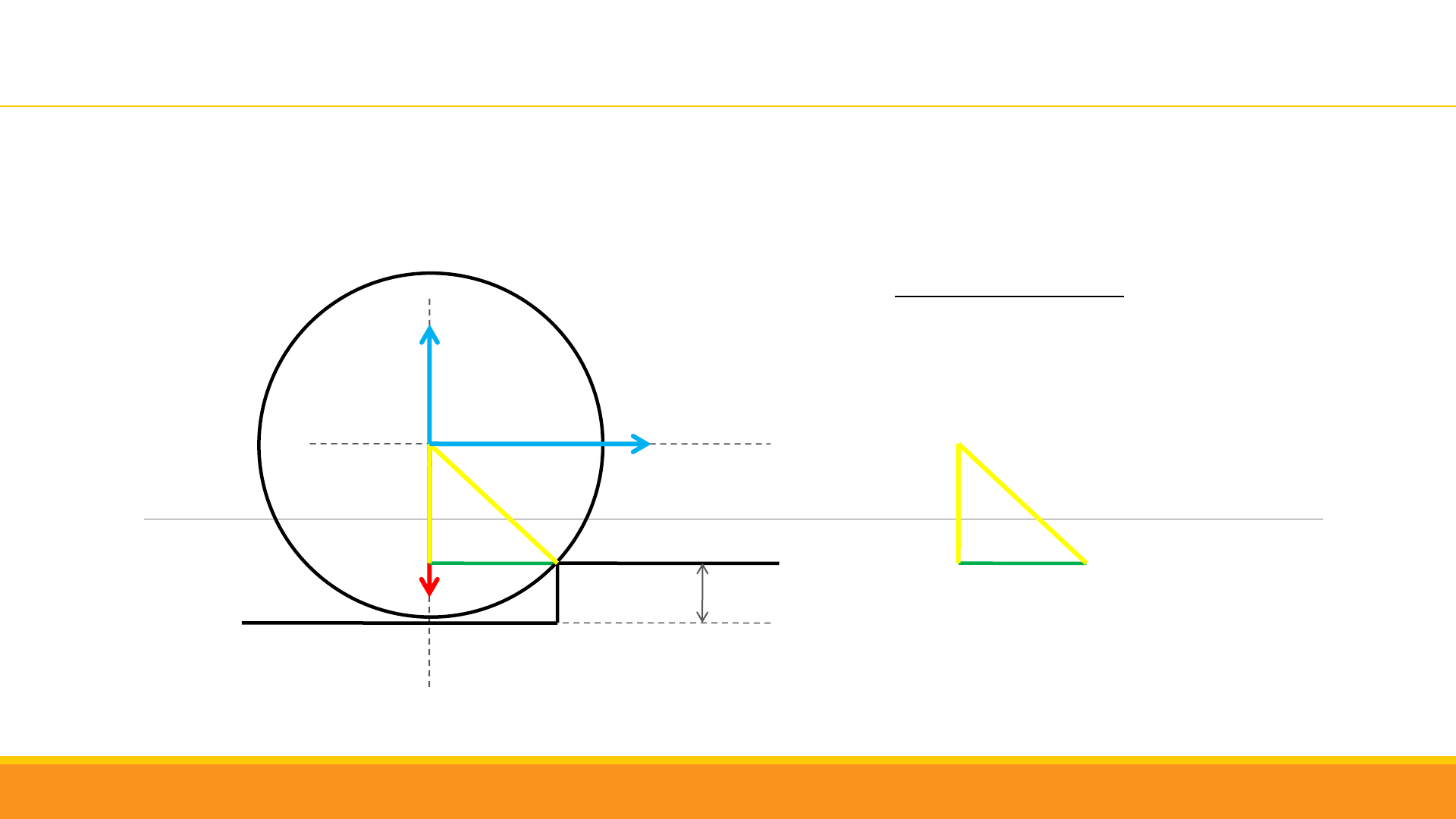
P
A
d
P
R
R – 0,1 m
d
P
0,2 m
0,3 m
2
+
0,2
2
=
0,3
2
=
0,3
2
0,2
2
= 0,22
0,1 m
F
y
F
x
FÍSICA I LIC. Y FARM. VIVIAN COGGIOLA
5
Se aplica sobre el eje de una rueda que pesa 100 N, una fuerza F que forma un ángulo de 30° con la horizontal, con el objeto
que la rueda pueda subir un escalón de 10 cm de alto, el radio de la rueda es de 30 cm. Calcular el valor mínimo de la
fuerza.
Ejemplo 1. Problema 6 guía educo
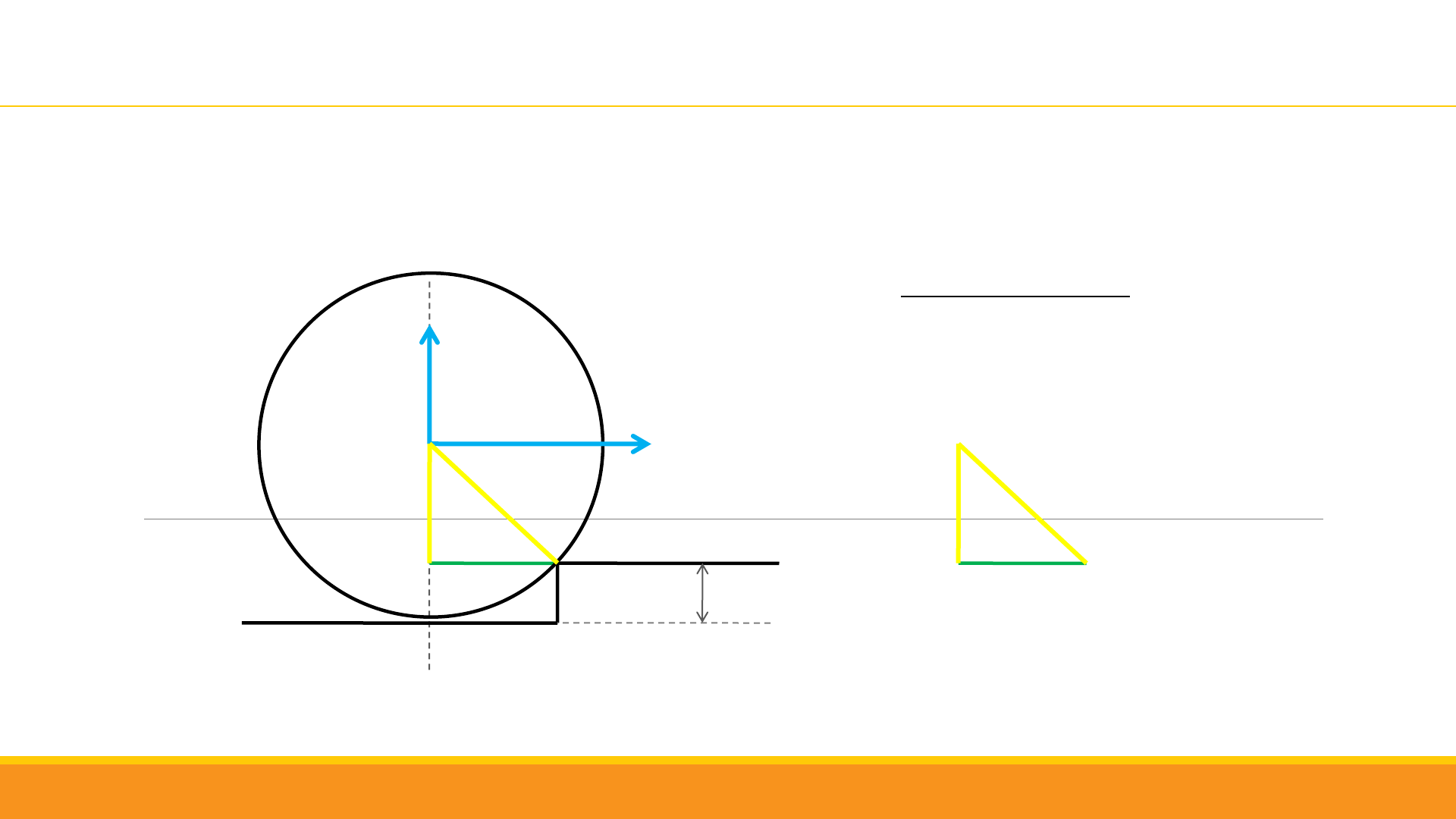
A
d
Fy
R
R – 0,1 m
d
Fy
0,2 m
0,3 m
2
+
0,2
2
=
0,3
2
=
0,3
2
0,2
2
= 0,22
0,1 m
F
y
F
x
FÍSICA I LIC. Y FARM. VIVIAN COGGIOLA
6
Se aplica sobre el eje de una rueda que pesa 100 N, una fuerza F que forma un ángulo de 30° con la horizontal, con el objeto
que la rueda pueda subir un escalón de 10 cm de alto, el radio de la rueda es de 30 cm. Calcular el valor mínimo de la
fuerza.
Ejemplo 1. Problema 6 guía educo
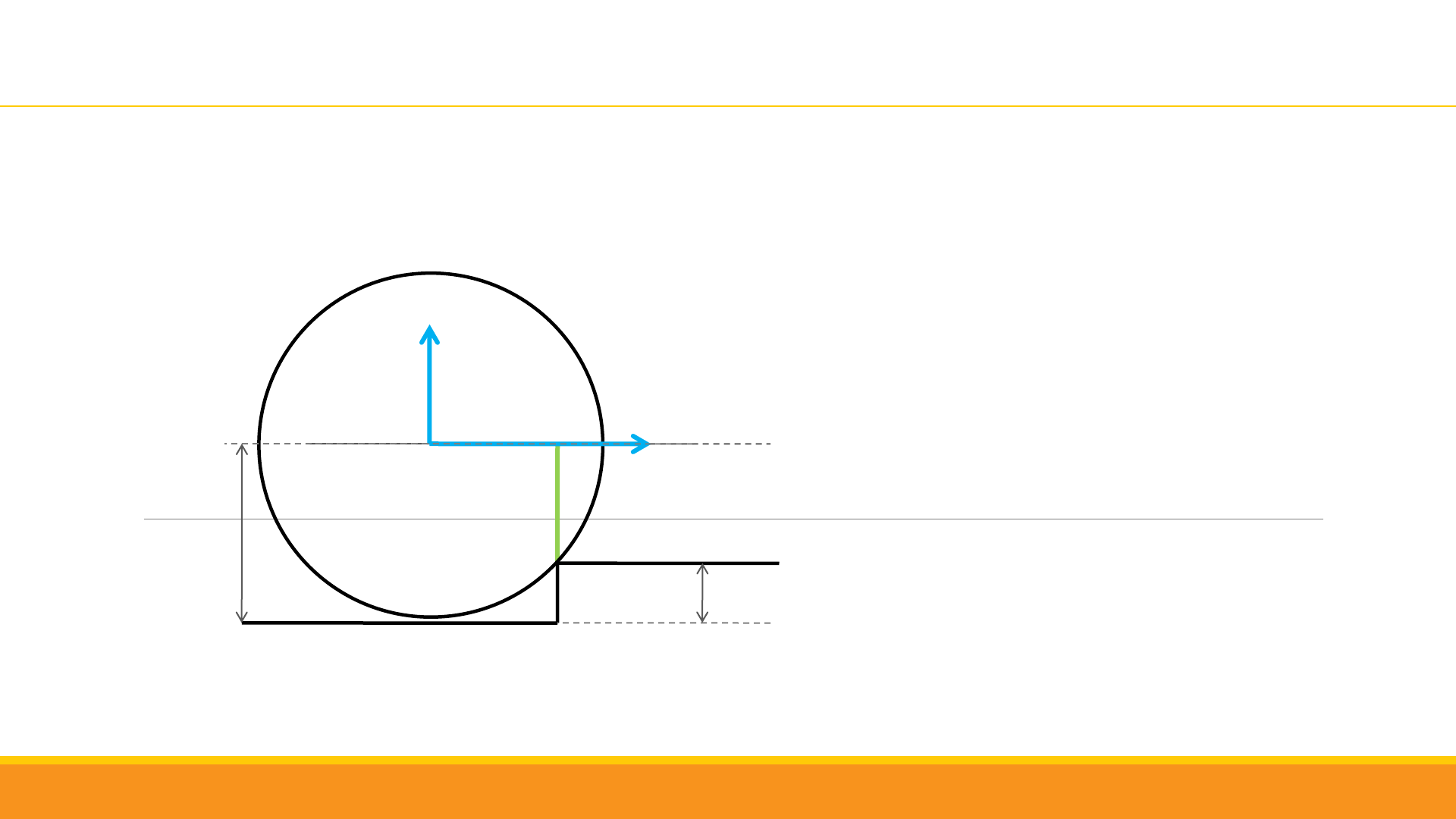
A
d
Fx
0,1 m
F
y
F
x
= 0,1
= 0,3 0,1
= 0,2
R = 0,3 m
FÍSICA I LIC. Y FARM. VIVIAN COGGIOLA
7
Se aplica sobre el eje de una rueda que pesa 100 N, una fuerza F que forma un ángulo de 30° con la horizontal, con el objeto
que la rueda pueda subir un escalón de 10 cm de alto, el radio de la rueda es de 30 cm. Calcular el valor mínimo de la
fuerza.
Ejemplo 1. Problema 6 guía educo
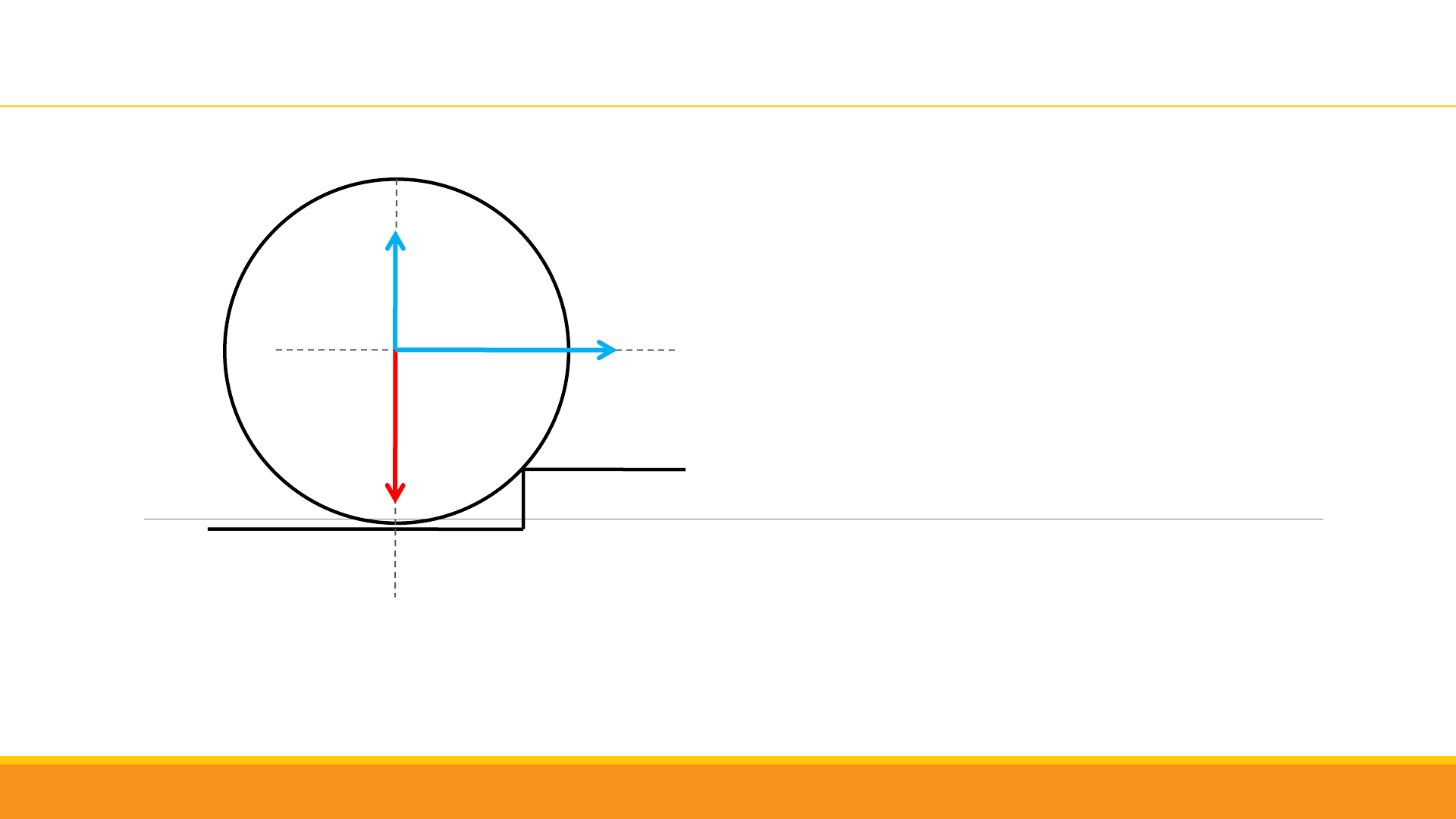
P
A
Condición de equilibrio estático:
Tomamos momento de torsión en
el punto A:
= 0
+
= 0
+
= 0
F
y
F
x
+ 1000,22
0,2
0,22 = 0
22
cos 30 0,2
sin 30 0,22 = 0
22 0,17 0,11 = 0
0,28 = 22
= ,
FÍSICA I LIC. Y FARM. VIVIAN COGGIOLA
8
Se aplica sobre el eje de una rueda que pesa 100 N, una fuerza F que forma un ángulo de 30° con la horizontal, con el objeto
que la rueda pueda subir un escalón de 10 cm de alto, el radio de la rueda es de 30 cm. Calcular el valor mínimo de la
fuerza.
Ejemplo 1. Problema 6 guía educo
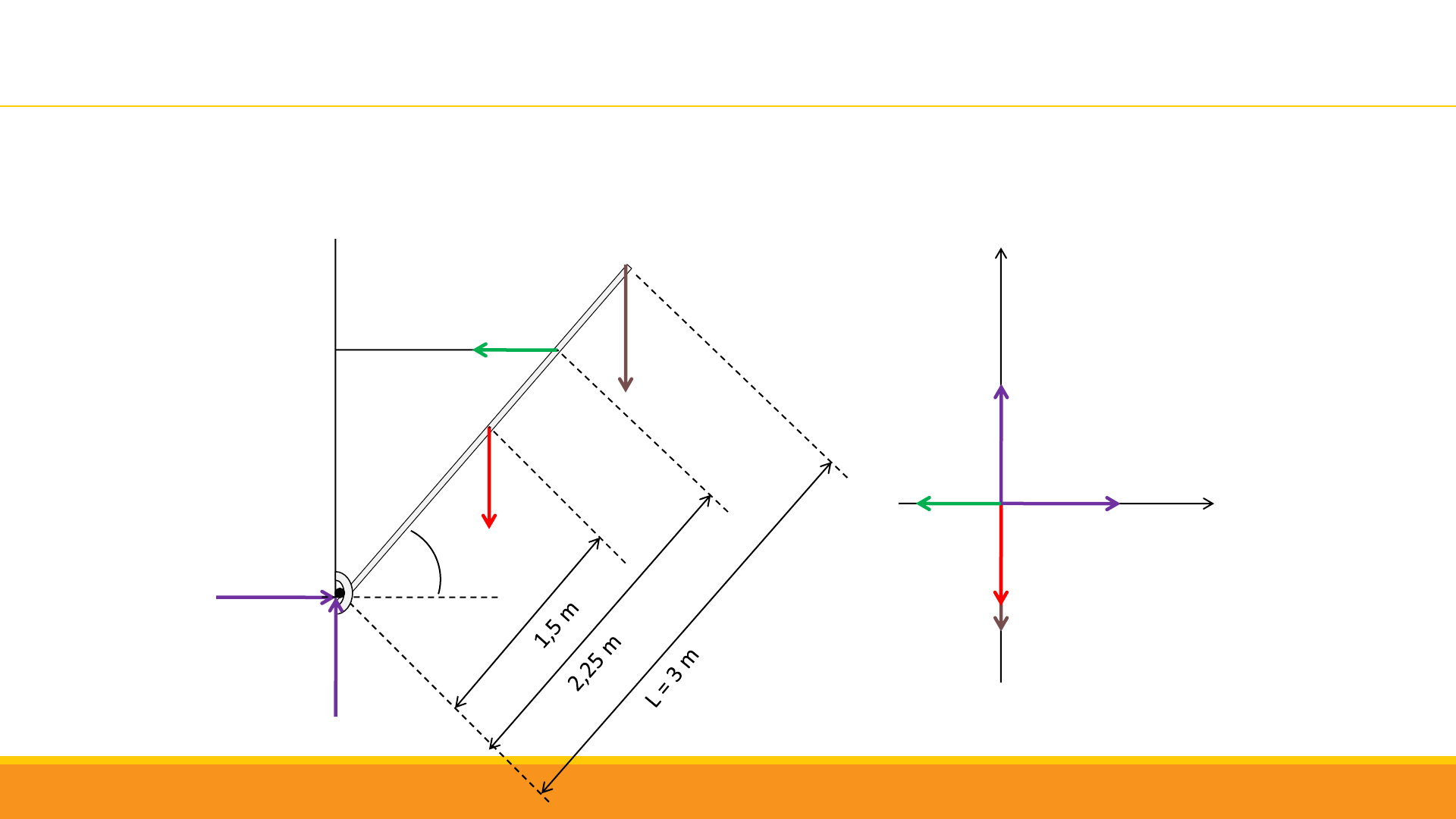
PR
H
R
V
50°
P = 400 N
T
2
P
R
V
R
H
y
x
T
1
T
1
T
2
= P
B
= 2000 N
FÍSICA I LIC. Y FARM. VIVIAN COGGIOLA
9
Un cuerpo de 2000 N está suspendido en equilibrio, soportado por una barra de peso 400N y una cuerda liviana, sujetos
ambos en la pared. Calcular las fuerzas reactivas en P que hace la barra y la fuerza S que realiza la cuerda. Datos: PO = 3 m
PB = 2,25 m PC = 1,50 m
Ejemplo 2. Problema 11 guía educo
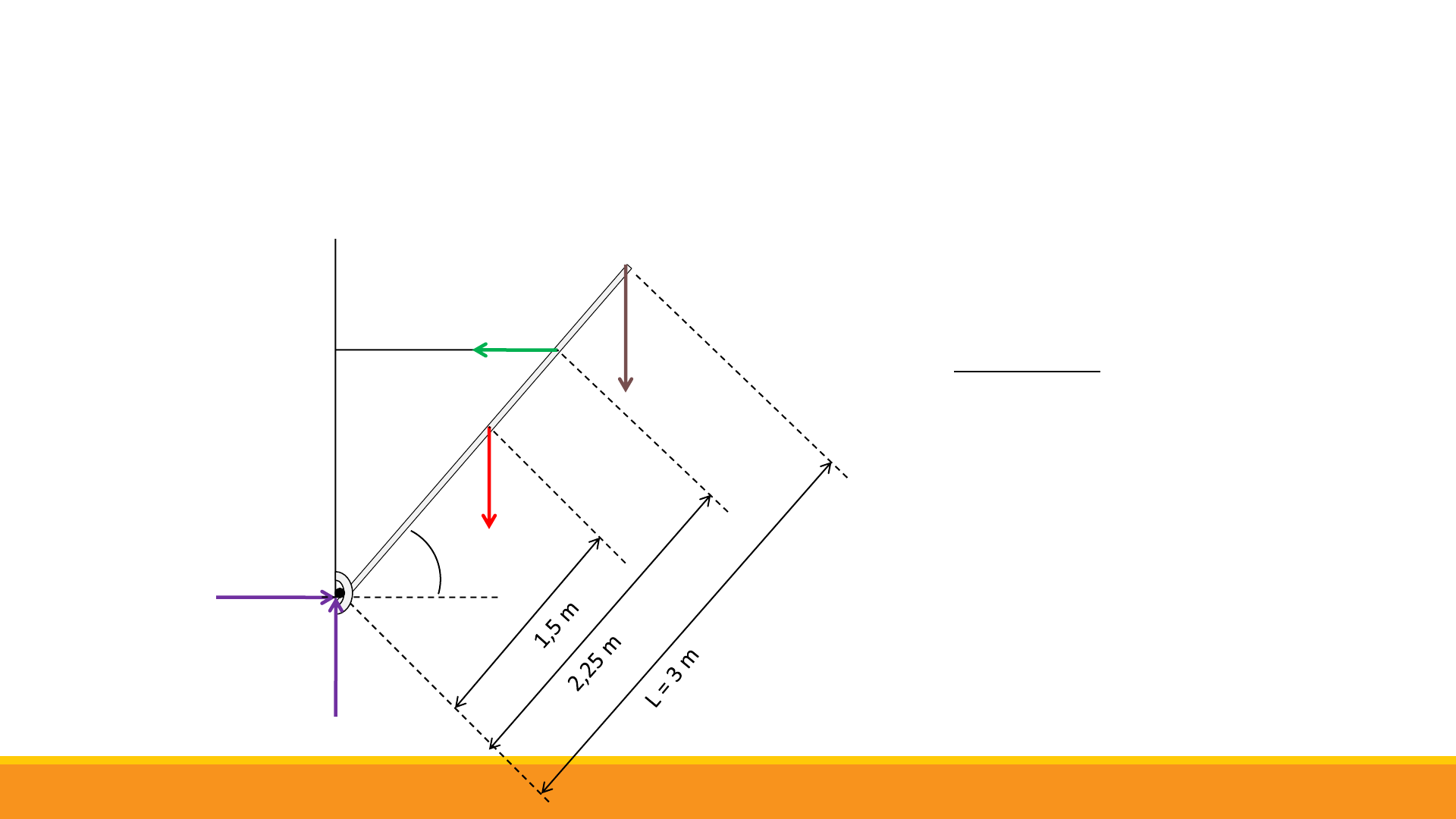
FÍSICA I LIC. Y FARM. VIVIAN COGGIOLA
10
Condición de equilibrioestático
PR
H
R
V
50°
P = 400 N
T
1
T
2
= 0
2
+
1
= 0
1,5 sin 40
2
3 sin 40
+
1
2,25 sin 50 = 0
1
=
4242,4
2,25 sin 50
TENSIÓN EN LA CUERDA 1
400 1,5 sin 40
2000 3 sin 40
+
1
2,25 sin 50 = 0
385,67
3856,73
+
1
2,25 sin 50 = 0
= ,
Condiciones de equilibrio estático
= 0
1
+
= 0
1
cos 180 +
cos 0 = 0
1
+
= 0
(1)
= 0
+
+
2
= 0
sin 90 + sin 270 +
2
sin 270 = = 0
400 2000 = 0
(2)
=
R
V
COMPONENTE VERTICAL DE LA
REACCIÓN EN LA BISAGRA
=
1
Reemplazamos T
1
en (1) :
= ,
R
H
COMPONENTE HORIZONTAL DE LA REACCIÓN
EN LA BISAGRA
11
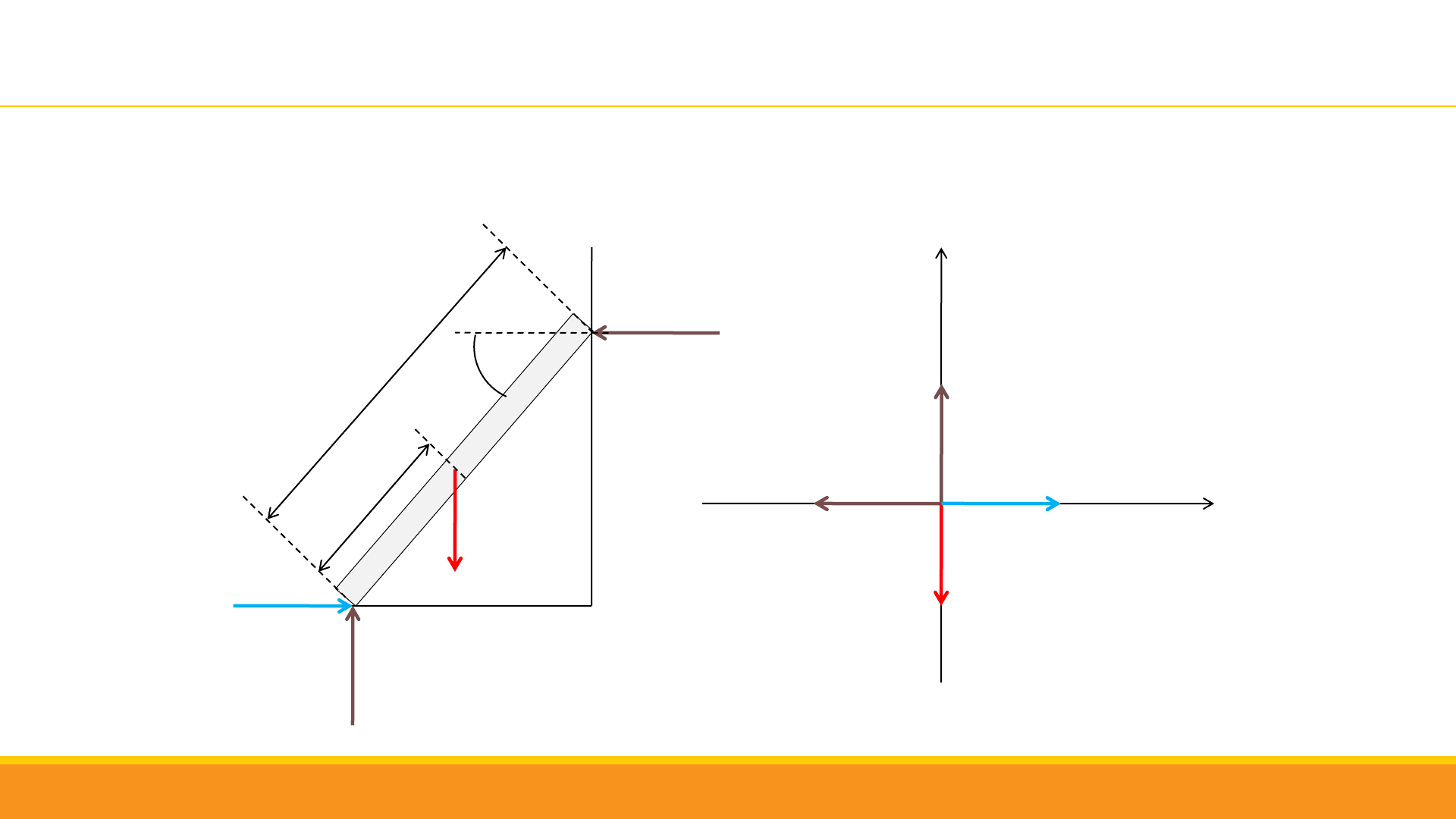
0,4 L
L
A
F
R
N
A
N
B
B
50°
P = 200 N
N
B
P
N
A
F
R
y
x
FÍSICA I LIC. Y FARM. VIVIAN COGGIOLA
12
Una escalera se apoya contra una pared lisa (sin rozamiento). La escalera pesa 200 N y su centro de gravedad está a 0,40 L,
medido desde el piso y a lo largo de la escalera, siendo L el largo de dicha escalera. Se pide: a) Calcular la fuerza reactiva de
la pared a la escalera. b) ¿Cuál debe ser la magnitud de la fuerza de fricción al pie de la escalera, para que ésta no resbale?
c) Calcular la reacción vertical del piso a la escalera.
Ejemplo 3. Problema 12 guía educo
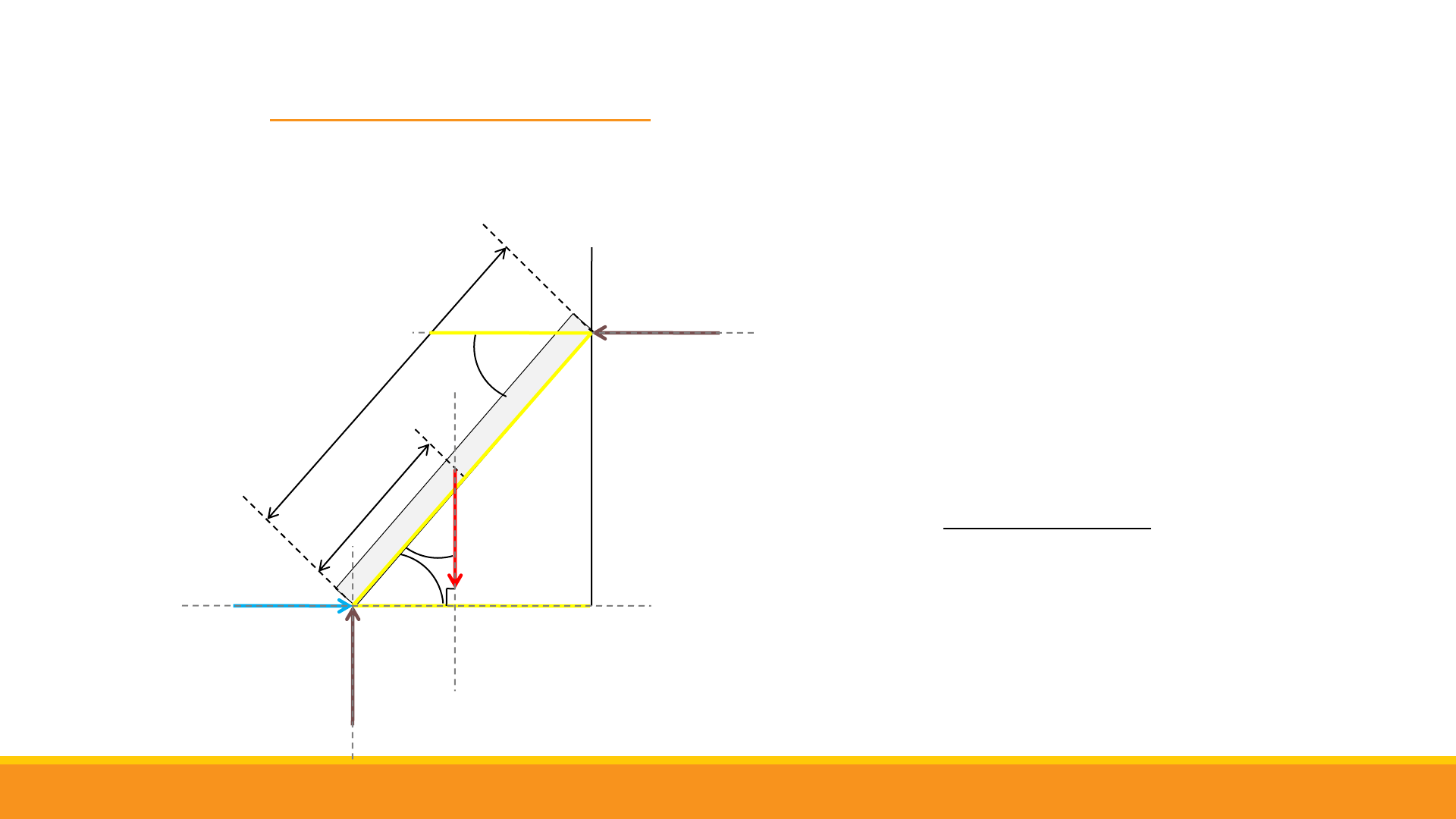
0,4 L
L
A
F
R
N
A
N
B
B
50°
P = 200 N
Condiciones de equilibrio estático
= 0
+
= 0
0,4 sin 40
+
sin 50 = 0
0,4 sin 40
+
sin 50
= 0
200 0,4 sin 40
+
sin 50 = 0
=
200 0,4 sin 40
sin 50
= ,
50°
40°
N
B
FUERZA REACTIVA DE LA PARED A LA ESCALERA
FÍSICA I LIC. Y FARM. VIVIAN COGGIOLA
13
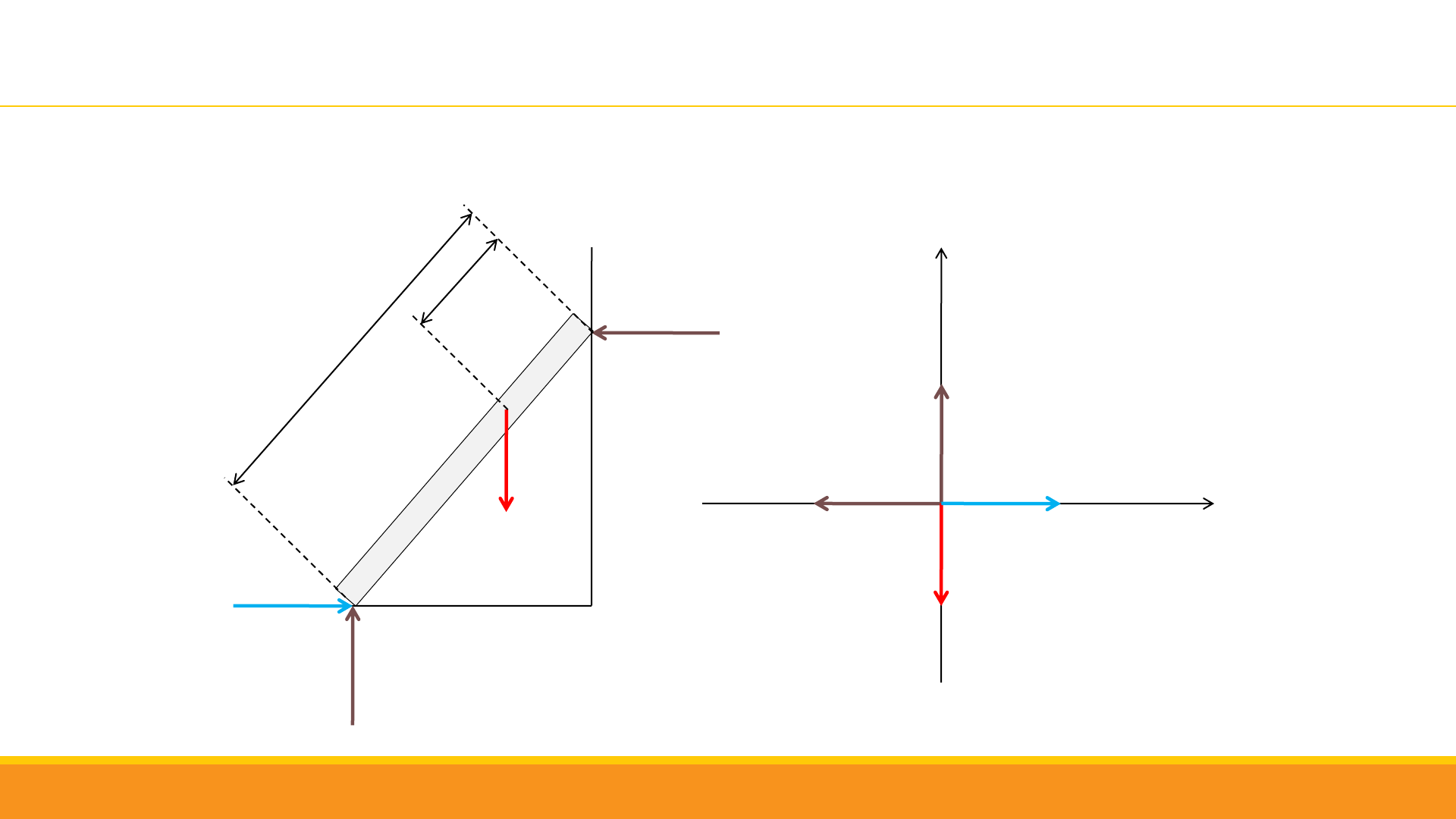
Condiciones de equilibrio estático
= 0
+
= 0
cos 180 +
cos 0 = 0
+
= 0
(1)
= 0
+
= 0
sin 90 + sin 270 = 0
= 0
(2)
= =
REEMPLAZAMOS N
B
EN (1) Y CALCULAMOS
LA FUERZA DE FRICCIÓN:
=
= ,
FÍSICA I LIC. Y FARM. VIVIAN COGGIOLA
14
0,6 m
L = 2m
α
F
R
N
A
N
B
B
Pb = 200 N
N
B
Pb
N
A
F
R
y
x
A
FÍSICA I LIC. Y FARM. VIVIAN COGGIOLA
15
Se tiene una barra de peso despreciable, de 2m de largo apoyada en una pared como muestra la figura, a 60 cm del
extremo superior cuelga un bloque de 200 N. Calcular el ángulo “α” mínimo que debe formar la barra con el piso para que
no se deslice. El μ
s
=0,2.
Ejemplo 4. Problema 18 guía educo
Este documento contiene más páginas...
Descargar Completo
Clase práctica Estática.pdf
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.