XI.-1
MAQUINAS ALTERNATIVAS Y TURBOMAQUINAS
CICLOS TERMICOS IDEALES
CICLO ATKINSON
El ciclo de Atkinson es una variante del ciclo de Otto donde no se
interrumpe el proceso de expansión, verificándose un mayor
aprovechamiento de la entalpía del fluido de trabajo, como se muestra en el
siguiente esquema.
Ciclo de combustión interna de Atkinson
UN POCO DE HISTORIA
El ciclo Atkinson fue propuesto y desarrollado por James
Atkinson en 1882.
La historia hace referencia a un intento de fabricar un motor de combustión
interna sin tener que pagar regalías a Otto por utilizar la idea de su ciclo, ni
a James Picard inventor del mecanismo biela manivela en 1780
La idea central de Atkinson, es desarrollar un ciclo con una relación de
expansión mayor a la de compresión de manera tal, que no deje escapar los
gases mientras la presión dentro del cilindro resulte superior a la presión
atmosférica.
Mientras que el motor que diseñó Atkinson no es más que una anécdota
histórica, el ciclo Atkinson está siendo utilizado en nuevos motores gracias
a que ofrece una importante mejora en el rendimiento con respecto al ciclo
de Otto.
La principal desventaja de un motor con ciclo Atkinson sobre el tradicional
de ciclo Otto es que ofrece menos potencia para igualdad de cilindrada.
El primer motor de combustión interna que operaba con este ciclo, lo
diseñó el propio Atkinson, utilizando un sistema mecánico en las bielas que
XI.-2
alargaba la carrera en la expansión, pero la mantenía en compresión, como
en un ciclo Otto, obteniendo así un trabajo extra que mejora el rendimiento.
Es importante destacar que el mecanismo patentado por Atkinson,
desarrollaba las cuatro carreras del ciclo en una sola vuelta del árbol de
cigüeñal.
Si, no es un error tipográfico, el embolo del motor desarrollaba cuatro
carreras, dos cortas y dos largas en tan solo una vuelta de cigüeñal.
La historia también registra algún intento de empleo de este ciclo en
turbomáquinas.
En efecto, las Turbinas de gas conocidas como turbinas de explosión,
funcionan según el ciclo ideal de Atkinson, y para su funcionamiento
utilizan:
• Un compresor.
• Una o más cámaras de combustión.
• La turbina de gas propiamente dicha.
El compresor carga sucesivamente con aire las cámaras de
combustión, estando controlado dicho orden por el mecanismo de la
válvula de admisión.
Cuando una cámara está cargada, se cierra la válvula de admisión y se
introduce el combustible, que se enciende por la acción de una chispa,
produciendo un incremento brusco de la presión.
A continuación se abre la válvula de escape y los gases salen a gran
velocidad, actuando directamente sobre los álabes de la turbina. La presión
disminuye y cuando se alcanza la presión atmosférica se cierra la válvula
de escape y se abre la de admisión llenándose nuevamente la cámara de
aire.
Las cámaras de combustión se disponen en una circunferencia concéntrica
con el eje de la turbina, disponiendo el funcionamiento de las válvulas de
tal manera que se descarguen sucesivamente, sometiendo a la corona de
álabes de la turbina a una serie de impulsos que provocan su movimiento.
El envío intermitente de gases calientes a la turbina, somete a los álabes de
la misma a un fuerte shock térmico y mecánico.
El funcionamiento de turbinas con este ciclo resultó muy poco racional,
determinando ello el abandono de este intento.
ACTUALIDAD
En la actualidad existen varios modelos de coches que montan un
motor que opera con el ciclo Atkinson, todos ellos en combinación con
motores eléctricos, dando lugar a los llamados coches híbridos.
XI.-3
Entre estos vehículos se destacan el Toyota Prius y el Auris HSD (las siglas
de Hybrid Synergy Drive), el Ford Escape, el Lexus RX 450h, el Hyundai
Sonata Hybrid y el Ford Evos Concept.
Citamos a continuación las prestaciones publicadas de algunos de ellos:
• Ford Escape Hybrid (2009): 2.5 153 CV, 7,84 l/100 km, relación
de compresión 12,3:1
• Toyota Prius II: 1,5lt, 78 CV, Potencia combinada híbrida 115
CV, Consumo 4,3 l/100 km, Relación de compresión 13:1
• Toyota Prius III: 1,8lt, 98 CV, Potencia combinada híbrida 134
CV, Consumo inferior a 4,3 l/100 km.
FUNCIONAMIENTO
Un motor que pretenda aprovechar las ventajas de este ciclo debe
presentar una alta relación de compresión volumétrica.
A los efectos de evitar anomalías en el proceso de combustión derivadas de
emplear una alta relación de compresión, se idearon ciertos "artificios" que
explotan las ventajas del ciclo, en la medida que consiguen un proceso de
expansión, mayor que el de compresión.
En la actualidad, esto se logra mediante un manejo adecuado (atraso) del
ángulo de cierre de las válvulas de admisión.
En la primera parte de la carrera de ascenso (compresión), el pistón sube y
la válvula de admisión permanece abierta.
En algún punto intermedio de la carrera, se cierra la válvula de admisión y
comienza la compresión efectiva.
A partir de ese punto, la compresión se desarrolla de forma normal. Pero
como el pistón ha estado subiendo con la válvula de admisión abierta, parte
del contenido del cilindro a retornado al conducto de admisión y solo se
comprime una cantidad reducida de gases.
Esta situación justifica las menores prestaciones de este tipo de motores,
comparado con uno de ciclo de Otto convencional
Operando de esta manera, la relación de compresión puede mantenerse tan
baja como resulte necesaria para evitar las combustiones anormales (como
en un motor ciclo de Otto), pero la relación de expansión, puede ser
bastante mayor, como en un motor Diesel, generando más trabajo con la
misma cantidad de combustible, o sea mejorando el rendimiento térmico.
La mezcla que retorna al conducto, queda almacenada en el conducto de
admisión y disponible para el siguiente ciclo de admisión.
Otra ventaja de trabajar sobre el ángulo de cierre de la válvula de admisión
es que ello permite regular la potencia de salida (carga) sin tener que
recurrir al estrangulamiento del motor, minimizando de ese modo las

XI.-4
pérdidas por bombeo, esto determina un aumento en el rendimiento
cualitativo del motor.
La incorporación de un sistema de inyección directa de combustible
contribuye a evitar eventuales pérdidas de combustible por el retroceso
antes indicado (solo vuelve aire) y para regular la potencia del motor
dosificando adecuadamente el combustible.
Es importante recordar que la inyección directa permite funcionar al motor
de encendido por chispa en condiciones de cargas parciales bajas, con
mezclas pobres, muy por debajo del límite de inflamabilidad.
En el caso que el motor aspire mezcla carburada (inyección o carburación
convencionales) se debe emplear un tubo de admisión con una cavidad y
una válvula automática (flaper) a efectos de permitir la funcionalidad del
sistema evitando pérdidas de mezcla.
Finalmente diremos que un motor funcionando en un vehículo híbrido lo
hará en condiciones estacionarias, situación que facilita la citada regulación
y su optimización.
CICLO ATKINSON TEORICO
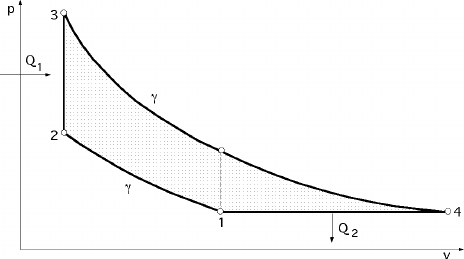
El ciclo teórico de Atkinson de expansión completa es una sucesión
de 4 transformaciones ideales, desarrolladas por un gas ideal (normalmente
aire) como se muestra en el siguiente esquema.
• La transformación 1-2 es una compresión adiabática.
• La transformación 2-3 es una Isométrica (el ciclo recibe calor)
• La transformación 3-4 es una expansión adiabática completa.
• La transformación 4-1 es una Isobárica (el ciclo entrega calor)
Donde

XI.-5
EF
c
MIN
V
r
V
=
Relación de compresión
MAX
e
MIN
V
r
V
=
Relación de expansión
33
22
Tp
Tp
==
Coeficiente de combustión a V Cte.
Además vamos a definir al coeficiente “
”
4
1
MAX
EF
VV
VV
==
Coeficiente de descarga a p Cte.
En este ciclo se tiene una relación de expansión, sensiblemente
mayor a la relación de compresión, el coeficiente “” nos indica
precisamente cuanto mayor es la relación de expansión respecto a la de
compresión por cuanto se verifica:
4
1
e
MAX
EF c
r
VV
V V r
==
RENDIMIENTO TERMICO
Desarrollemos a continuación un algoritmo de cálculo para el
rendimiento del ciclo teórico.
Partimos de la expresión general para el rendimiento térmico de un ciclo en
función de los calores intercambiados:
1
F
t
C
Q
Q
=−
El calor aportado al ciclo en la transformación 2-3 se calcula mediante:
32
()
Cv
Q mc T T=−
Y el calor sustraído al ciclo en la transformación 4-1 mediante:
41
()
Fp
Q mc T T=−

XI.-6
Reemplazando nos queda:
41
32
()
1
()
p
t
v
mc T T
mc T T
−
=−
−
Simplificando las masas, podemos poner:
41
32
()
1
()
p
t
v
c T T
c T T
−
=−
−
Factorizando convenientemente
4
1
1
3
2
2
1
1
1
p
t
v
T
T
c
T
c
T
T
T
−
=−
−
Utilizando las siguientes relaciones conocidas
p
v
c
k
c
=
y
3
2
T
T
=
Y teniendo en cuenta la transformación isobárica 4-1
44
11
TV
TV
==
Definido al comienzo
Nos queda
1
2
( 1)
1
( 1)
t
T
k
T
−
=−
−
De acuerdo con la transformación adiabática de compresión 1-2 podemos
escribir:
1
12
1
21
1
k
k
c
TV
T V r
−
−
==
Con lo que resulta la expresión particular:

XI.-7
1
1 ( 1)
1
( 1)
t
k
c
k
r
−
−
=−
−
CICLO ATKINSON TEORICO
Que permite calcular el rendimiento térmico teórico del ciclo de
Atkinson de expansión completa en función de la relación de compresión
“r
c
”, el exponente de la transformación adiabática “k” y de la relación de
descarga a presión constante “”
Es importante mostrar que el valor del coeficiente “” puede calcularse en
función del coeficiente de combustión a volumen constante “”
En efecto, considerando las adiabáticas de expansión y de compresión
respectivamente, podemos poner:
1
2
21
k
p
V
pV
=
y
3
4
43
k
p
V
pV
=
Multiplicando miembro a miembro ambas expresiones
13
24
2 4 1 3
k
pp
VV
p p VV
=
De acuerdo con la transformación isométrica 2-3 y la isobárica 4-1 resulta
41
pp=
y
23
VV=
De donde
3
4
21
k
p
V
pV
=
k
=
o bien
1/ k
=
Una evaluación cuantitativa de este ciclo nos muestra que el volumen
máximo resulta 3 a 4 veces mayor al denominado volumen efectivo “V
EF
”
que es aquel desde donde comienza la compresión efectiva, determinando
ello una muy elevada relación de expansión del orden de 30:1 a 40:1.

XI.-8
En el gráfico siguiente se muestran los valores del rendimiento térmico
teórico para los ciclos teóricos Otto y Atkinson calculados para la misma
relación de compresión y para un mismo valor de la relación de combustión
a volumen constante (=4)
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
imiento térmico [adim]
COMPARATIVO RENDIMIENTO DE CICLOS
Se observa una mejora importante en el rendimiento para todo el
rango de relaciones de compresión. Para un valor 10:1 de la relación de
compresión, muy usada en este tipo de motores, la mejora en el
rendimiento alcanza un 14%

XI.-9
CICLO ATKINSON DE EXPANSION PARCIAL
Cuando se trabaja en la construcción de un motor que opere de
acuerdo al ciclo de Atkinson el concepto de expansión completa resulta
difícil de implementar y hasta perjudicial sobre el rendimiento de la
máquina real, puesto que la mejora en el rendimiento de ciclo límite, no
alcanza a compensar la pérdida de rendimiento mecánico que se origina
como consecuencia del aumento de tamaño del motor.
Por tal motivo estudiaremos el caso de una variante que llamaremos “Ciclo
Atkinson de expansión parcial” que es en esencia un ciclo teórico mixto
entre el ciclo de Otto y el Atkinson de expansión total.
El ciclo teórico de Atkinson de expansión parcial es una sucesión de 5
transformaciones ideales como se muestra en el siguiente esquema.
En el mismo se observa que el proceso de expansión, si bien es
mayor al del ciclo de Otto, se ha interrumpido antes de llegar a la presión
atmosférica, resultando de ese modo dos transformaciones con cesión de
calor al medio para volver a las condiciones ideales.
• La transformación 1-2 es una compresión adiabática.
• La transformación 2-3 es una Isométrica (el ciclo recibe calor)
• La transformación 3-4 es una expansión adiabática.
• La transformación 4-5 es una Isométrica (el ciclo entrega calor)
• La transformación 5-1 es una isobárica (el ciclo entrega calor)
Esta modificación permite bajar el valor de la relación de expansión
a valores de entre 15:1 a 20:1 donde se verifican los mejores resultados
prácticos.
En este caso vamos a considerar las siguientes relaciones:

XI.-10
EF
c
MIN
V
r
V
=
Relación de compresión
MAX
e
MIN
V
r
V
=
Relación de expansión
33
22
Tp
Tp
==
Coeficiente de combustión a V Cte.
5
1
e
MAX
EF c
Vr
V
V V r
= = =
Coeficiente de descarga a p Cte.
Pero además vamos a definir a la relación “”
44
55
pT
pT
==
Coeficiente de descarga a V Cte.
Más adelante veremos que ambos coeficientes están relacionados
entre sí y con el coeficiente de combustión a volumen constante “”
mediante la siguiente expresión:
k
=
RENDIMIENTO TERMICO
Partimos de la expresión general para el rendimiento térmico de un
ciclo en función de los calores intercambiados:
1
F
t
C
Q
Q
=−
El calor aportado al ciclo en la transformación 2-3 se calcula mediante:
32
()
Cv
Q mc T T=−
Y el calor sustraído al ciclo tiene dos componentes, una fracción a
Volumen constante y otra a presión constante:
F V p
Q Q Q=+
Para la transformación de descarga a volumen contante 4-5 tenemos:
45
()
VV
Q mc T T=−

XI.-11
Y para la transformación de descarga a presión contante 5-1 tenemos:
51
()
pp
Q mc T T=−
Reemplazando nos queda:
4 5 5 1
32
( ) ( )
1
()
vp
t
v
mc T T mc T T
mc T T
− + −
=−
−
Simplificando y reordenando podemos poner:
4 5 5 1
32
( ) ( )
1
()
t
T T k T T
TT
− + −
=−
−
Factorizando convenientemente
41
55
55
3
2
2
11
1
1
t
TT
T kT
TT
T
T
T
− + −
=−
−
Utilizando las siguientes relaciones conocidas
p
v
c
k
c
=
;
3
2
T
T
=
;
4
5
T
T
=
y
5
1
T
T
=
Nos queda
5
2
( 1) (1 1 )
1
( 1)
t
T
k
T
− + −
=−
−
Multiplicando y dividiendo convenientemente por T
1
resulta
5
1
12
( 1) (1 1 )
1
( 1)
t
T
T
k
TT
− + −
=−
−
Recordando que:
1
12
1
21
1
k
k
c
TV
T V r
−
−
==
y
5
1
T
T
=
Podemos poner:
1
( 1) (1 1 )
1
( 1)
t
k
c
k
r
−
− + −
=−
−
O bien
1
1 ( 1) (1 1 )
1
( 1)
t
k
c
k
r
−
− + −
=−
−

XI.-12
Desarrollando el segundo término del numerador dentro del corchete:
1
1 ( 1) ( )
1
( 1)
t
k
c
kk
r
−
− + −
=−
−
Y factorizando nos queda:
1
1 ( 1) ( 1)
1
( 1)
t
k
c
k
r
−
− + −
=−
−
ATKINSON CON EXPANSION PARCIAL
Si analizamos la expresión del rendimiento del ciclo teórico de
Atkinson con expansión parcial vemos que se trata de una función
( , , )
tc
f r k y
=
Que presentará algunas condiciones límites dependiendo de los
valores que tomen los coeficientes
y
respectivamente
CASO 1)
Anulamos la componente de descarga a V Cte.
( 1)
=
Entonces el punto 4 coincide con el punto 5 y el ciclo toma el aspecto del
ciclo de Atkinson con expansión completa, que es el límite superior del
caso en estudio.
La expresión hallada se reduce a:
1
1 ( 1)
1
( 1)
t
k
c
k
r
−
−
=−
−
CICLO ATKINSON TEORICO
Nos queda la expresión correspondiente al rendimiento del ciclo de
Atkinson con expansión completa que es el límite superior del caso en
estudio.
CASO 2)
Ahora anulamos la componente de descarga a p Cte. (
= 1)
Entonces es el punto 5 el que coincide con el punto 1 y el ciclo toma el
aspecto del ciclo Otto.
La expresión hallada queda en tal caso:

XI.-13
Si
1
= =
resulta
1
1 ( 1)
1
( 1)
t
k
c
r
−
−
=−
−
Expresión correspondiente al ciclo de Otto, que es el límite inferior
del caso en estudio.
RELACION ENTRE LOS COEFICIENTES
;
y
Los citados coeficientes fueron definidos como relaciones de las
transformaciones isométricas 2-3 y 4-5 y la isobárica 5-1 respectivamente
de la siguiente manera:
33
22
Tp
Tp
==
;
55
44
Tp
Tp
==
y
55
11
Tp
Tp
==
Considerando las transformaciones adiabáticas de expansión 3-4 y de
compresión 1-2, podemos poner:
3
4
43
k
p
V
pV
=
y
21
12
k
pV
pV
=
Dividiendo miembro a miembro ambas expresiones
31
42
4 2 3 1
k
pp
VV
p p V V
=
De acuerdo con las transformaciones isométricas 2-3 y 4-5 y la
isobárica 4-1 resulta:
23
VV=
;
45
VV=
y
51
pp=
Simplificando los volúmenes V
2
y V
3
y reemplazando convenientemente
De donde
3 5 5
2 4 1
k
p p V
p p V
=

XI.-14
1
k
=
o bien
k
=
Para terminar diremos que en el análisis detallado del rendimiento de
un motor real, lo primero que tenemos que conocer es el rendimiento del
ciclo límite, o sea del ciclo ideal con el que vamos a comparar su
desempeño.
El ciclo límite es un ciclo ideal condicionado para algunas cuestiones de la
realidad. Es en este contexto, donde cobra real importancia el valor de la
relación “” ya que su valor no es arbitrario, sino que depende del aporte
máximo de energía que puede obtenerse por combustión completa con el
aire disponible al final de la etapa de compresión.
REPRESENTACION DEL CICLO ATKINSON TEORICO
Con el objetivo de representar gráficamente y en escala el desarrollo
de un ciclo teórico de Atkinson utilizaremos una hoja de cálculo (se adjunta
archivo Excel) donde se analiza el caso particular de un motor de 1900cm
3
con una cámara de combustión de 100cm
3
y una relación de compresión
volumétrica de 20:1 con la particularidad de que la compresión efectiva
comienza cuando el pistón a recorrido algo más de la mitad del volumen
del cilindro.
Concretamente tomamos como punto inicial del ciclo (1 en el diagrama) a
aquel donde el volumen dentro del reactor es de 1000cm
3
y el gas está a la
presión atmosférica normal y a una temperatura de 20C
El volumen efectivo es entonces de 1000cm
3
La relación de compresión resulta de 10:1 y la relación de expansión es de
20:1.
A continuación se calculan las propiedades del gas para una serie de
estados que permitan graficar al ciclo completo tanto en el diagrama
mecánico (pV) como en el diagrama del calor (TS)
En primer lugar se calculan una serie de estados para graficar la
compresión adiabática 1-2.
Allí consideramos un aporte de calor correspondiente al máximo teórico
que se obtiene por combustión de gasolina con la cantidad de aire
disponible aplicando la relación estequiométrica.
Se calculan entonces una nueva serie de estados para graficar la
transformación isométrica 2-3 donde se alcanza el punto de máxima
entalpía del fluido de trabajo.
Continuamos entonces con el cálculo de estados sobre la transformación de
expansión adiabática 3-4 que culmina cuando alcanzamos el volumen
máximo fijado en 2000cm
3
.

XI.-15
Es importante notar que en el caso propuesto para el estudio no llegamos
con la expansión a la presión atmosférica, pero vamos hasta presiones
bastante mas bajas que el Otto equivalente de mitad de cilindrada.
Luego calculamos una serie de estados para graficar la transformación
isométrica de escape 4-5 hasta alcanzar la presión atmosférica y finalmente
algunos puntos de la isobárica de enfriamiento 5-1 que permite volver a las
condiciones ideales.
En la tabla de datos se han calculado la presión, el volumen, la temperatura
y la entropía de cada punto.
Esto permite por un lado graficar los ciclos en el diagrama mecánico (p-V)
y en el diagrama del calor o (T-S).
Además en la hoja de cálculos se realiza una determinación del rendimiento
del ciclo recurriendo a una integración numérica sobre el diagrama
entrópico y finalmente una verificación haciendo lo propio en el diagrama
mecánico.
El valor obtenido para el rendimiento térmico del ciclo teórico de Atkinson
con expansión parcial es de:
68,70%
Atkinson parcial
=
Mientras que el Otto equivalente presenta un rendimiento térmico teórico
de:
60,17%
Otto
=
Y el Atkinson de expansión completa:
71,68
Atkinson
=
Rendimiento del motor naftero de 4T.doc
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.