213
SUPERFICIES
8.1. Definición
Se llama superficie al conjunto de puntos del espacio, y solamente a
aquellos, que satisfacen una ecuación rectangular (cartesiana) de la forma:
f(x, y, z) = 0
Esta definición establece que si una ecuación de la forma f(x, y, z) = 0
representa un lugar geométrico, ese lugar geométrico es una superficie y
viceversa, si una superficie puede representarse analíticamente por una
ecuación, esa ecuación es de la forma f(x, y, z) = 0.
Por ejemplo, un plano es una superfície, se vió que su ecuación general
es de la forma: Ax + By + Cz + D = 0 o sea una ecuación con tres vari-
ables. La Fig. 8.1. representa el plano de ecuación: 3x – 2y + 4z – 6 = 0.
La ecuación y − 5 = 0 también representa un plano.(Fig. 8.2.)
214
En ella no intervienen las tres variables. O sea que en la ecuación de una
superficie no siempre van a figurar las tres variables.
Debe aclararse que una ecuación de la forma f(x, y, z) = 0 no siempre
representa una superficie. Por ejemplo, dada la ecuación:
05zyx
222
=+++
no existen valores reales de x, y, z que satisfagan esa ecuación, por lo
tanto esa ecuación no representa ningún lugar geométrico real.
8.2. Superficie de revolución
Una superficie de revolución es la engendrada por la rotación de una
curva plana, en torno a una recta fija contenida en el plano de esa curva.
Por ejemplo la superficie esférica es una superficie de revolución porque
se genera por la rotación de una circunferencia alrededor de uno de sus
diámetros.
En la Fig. 8.3. se observa una su-
perficie esférica generada por la
rotación de una circunferencia
alrededor del diámetro
MN
215
En la Fig. 8.4 se observa una su-
perficie (elipsoide de revolución)
generada por la rotación de una
elipse alrededor de su eje mayor
MN
Al hacer el análisis de las superficies que se estudiarán a lo largo de este
capítulo se irá indicando cuáles de ellas son superficies de revolución.
8.3. Superficies regladas
Una superficie reglada es aquella que puede ser engendrada por el movi-
miento de una recta.
Por ejemplo, en la Fig. 8.5. la recta ℓ se mueve paralela a sí misma según
la dirección de la recta
ɡ. La superficie generada es un plano, por lo tanto
un plano es una superficie reglada.
También en este caso, al hacer el análisis de las superficies se irá indican-
do cuáles de ellas son superficies regladas.
216
8.4. Análisis de una superficie
Para el análisis de una superficie se tendrán en cuenta los siguientes 6
puntos:
I. Hallar las intersecciones con los ejes coordenados
II. Determinar las trazas sobre los planos coordenados
III. Estudiar la simetría con respecto a los planos coordenados, a los
ejes coordenados y al origen de coordenadas.
IV. Determinar las secciones con planos paralelos a los planos coor-
denados y la extensión de la superficie
V. Indicar si es superficie de revolución
VI. Indicar si es superficie reglada
8.4.1. Intersecciones con los ejes coordenados
217
Intersección con el eje
Ox
: Puesto que todos los puntos del eje x tienen su
segunda y tercera coordenadas iguales a 0, la intersección se obtiene re-
emplazando en la ecuación de la superficie las variables y y z por 0.
Intersección con el eje
Oy
: Puesto que todos los puntos del eje y tienen su
primera y tercera coordenadas iguales a 0, la intersección se obtiene re-
emplazando en la ecuación de la superficie las variables x y z por 0.
Intersección con el eje
Oz
: Puesto que todos los puntos del eje z tienen su
primera y segunda coordenadas iguales a 0, la intersección se obtiene
reemplazando en la ecuación de la superficie las variables x e y por 0.
Las intersecciones del plano 3x – 4y + 6z − 12 = 0 con cada uno de los
ejes coordenados son, respectiva-
mente:
Eje
=
=
=−+−
0z
0y
0126z4y3x
Ox :
⇒ 3x = 12 ⇒ x = 4.
La intersección es el punto (4, 0, 0)
Eje
=
=
=−+−
0z
0x
0126z4y3x
Oy :
x = z = 0 ⇒ −4y = 12 ⇒ y =−3.
La intersección es el punto (0, −3, 0)
218
Eje
=
=
=−+−
0y
0x
0126z4y3x
Oz:
x = y = 0 ⇒ 6z = 12 ⇒ z = 2. La intersección es el punto (0, 0, 2)
8.4.2. Trazas sobre los planos coordenados
Traza sobre el plano XY (T
XY
): Puesto que todos los puntos del plano XY
tienen su tercera coordenada igual a 0, la traza (intersección) se obtiene
igualando, en la ecuación de la superficie, la variable z a 0.
Traza sobre el plano XZ (T
XZ
): Puesto que todos los puntos del plano XZ
tienen su segunda coordenada igual a 0, la traza (intersección) se obtiene
igualando, en la ecuación de la super-
ficie, la variable y a 0.
Traza sobre el plano YZ (T
YZ
): Puesto
que todos los puntos del plano YZ
tienen su primera coordenada igual a
0,
la traza (intersección) se obtiene igua-
lando, en la ecuación de la superficie,
la variable x a 0.
Sea el plano 3x – 4y + 6z − 12 = 0.
Sus trazas sobre cada uno de los pla-
nos coordenados son (Fig.8.7.):
Con el plano XY
z = 0 ⇒ 3x – 4y − 12 = 0
219
=
=−−
0z
0124y3x
:T
XY
Con el plano YZ
x = 0 ⇒ – 4y + 6z − 12 = 0
=
=−+−
0x
0126z4y
:T
YZ
Con el plano XZ
y = 0 ⇒ 3x + 6z − 12 = 0
=
=−+
0y
0126z3x
:T
XZ
8.4.3 Simetría
a) Respecto del origen de coordenadas
Si la ecuación de una superficie no cambia al reemplazar la variable x por
(−x) , la variable y por (−y) y la variable z por (−z), la superficie es simé-
trica respecto del origen de coordenadas.
El paraboloide elíptico de ecuación
4y3z2x
22
−=+
no es simétrico
respecto del origen de coordenadas ya que
( ) ( ) ( )
y4z3x2
22
−−=−+−
no es igual a la ecuación dada.
b) Respecto de los ejes coordenados
Si la ecuación de una superficie no cambia al reemplazar la variable x por
(−x) y la variable y por (−y), la superficie es simétrica respecto del eje z.
Si la ecuación de una superficie no cambia al reemplazar la variable x por
(−x) y la variable z por (−z), la superficie es simétrica respecto del eje y.
220
Si la ecuación de una superficie no cambia al reemplazar la variable y por
(
−y) y la variable z por (−z), la superficie es simétrica respecto del eje x.
Por ejemplo, el paraboloide elíptico de ecuación
4y3z2x
22
−=+
es
simétrico respecto del eje y pero no respecto del eje x, ni del eje z.
En efecto:
( ) ( )
⇒−=−+− 4yz3x2
22
4y3z2x
22
−=+
(simetría res-
pecto del eje y).
( ) ( )
⇒−−=−+ y4z32x
2
2
4y3z2x
22
=+
(no hay simetría
respecto del eje x).
( ) ( )
⇒−−=+− y43zx2
2
2
4y3z2x
22
=+
(no hay simetría
respecto del eje z).
Fig.8.8
221
c) Respecto a los planos coordenados
Si la ecuación de una superficie no cambia al reemplazar la variable z por
(−z), la superficie es simétrica respecto del plano XY.
Si la ecuación de una superficie no cambia al reemplazar la variable y por
(−y), la superficie es simétrica respecto del plano XZ.
Si la ecuación de una superficie no cambia al reemplazar la variable x por
(
−x), la superficie es simétrica respecto del plano YZ.
Por ejemplo, como se verá al estudiar los paraboloides, el paraboloide
elíptico de ecuación
4y3z2x
22
−=+
es simétrico respecto del plano YZ
y respecto del plano XY, pero no respecto del plano XZ. Fig.8.8.
En efecto:
( )
⇒−=+− 4y3zx2
2
2
4y3z2x
22
−=+
(La superficie es simétrica respecto del plano YZ)
( )
⇒−=−+ 4yz32x
2
2
4y3z2x
22
−=+
(La superficie es simétrica respecto del plano XY)
( )
⇒−−=+ y43z2x
22
4y3z2x
22
=+
(La superficie no es simétrica respecto del plano YZ)
8.4.4. Intersecciones con planos paralelos a los planos coordenados
Con planos paralelos al plano XY
Se trata de encontrar la intersección de la superficie con planos cuya
ecuación sea de la forma z = k.
Con planos paralelos al plano XZ
Se trata de encontrar la intersección de la superficie con planos cuya
ecuación sea de la forma y = k.
Con planos paralelos al plano YZ
222
Se trata de encontrar la intersección de la superficie con planos cuya
ecuación sea de la forma x = k.
8.4.5. Extensión
Para cada uno de los casos planteados en el punto anterior se indican los
valores de k, para los cuales se obtiene un lugar geométrico real.
8.5. Estudio analítico de distintas superficies
A continuación se irán dando las definiciones, el análisis, la gráfica y
ejemplos de distintas superficies cuya ecuación es de 2º grado.
Pero debe aclararse que, salvo en el caso de la superficie esférica, sólo se
estudiarán aquellas ecuaciones que representan superficies cuyo eje es
alguno de los ejes coordenados.
8.5.1. Superficie esférica
Se llama superficie esférica al lugar geométrico de los puntos del espacio
que equidistan de un punto fijo llamado centro.
C(α, β, γ)
RPC =
La ecuación de una superficie esférica de centro C y radio R es:
223
( ) ( )
( )
2
222
Rγzβyαx =−+−+−
Ejemplo: (x − 2)
2
+ (y + 4)
2
+ (z − 3)
2
= 4 (Fig.8.9.)
es una superficie esférica de centro C(2,-4,3) y radio 2
Si el centro está en el origen, la ecuación de la superficie esférica es:
x
2
+ y
2
+ z
2
= R
2
A continuación se hará el análisis de esta ecuación siguiendo los pasos
indicados en los puntos anteriores (Fig.8.10).
I) Intersecciones con los ejes coordenados
Ecuación
x
2
+ y
2
+ z
2
= R
2
Eje
=
=
=++
0z
0y
Rzx
Ox
222 2
:
y
⇒ x
2
= R
2
⇒ x = ± R
Dos puntos
( )
( )
R,0,0
R,0,0
−
Eje
=
=
=++
0z
0x
Rzx
Oy
222 2
:
y
⇒ y
2
= R
2
⇒
y = ± R
Fig.8.10
224
Dos puntos
( )
( )
R,0
R,00,
−,0
Eje
=
=
=++
0y
0x
Rzx
Oz
222 2
:
y
⇒ z
2
= R
2
⇒ z = ± R
Dos puntos
( )
( )
R
R0,0,
−,0,0
II) Trazas sobre los planos coordenados
Traza sobre el plano XY:
T
XY
:
=++
=
222
Ryx
0z
2
z
⇒ Circunferencia
=+
=
222
Ryx
0z
Traza sobre el plano XZ:
T
XZ
:
=++
=
222
Ryx
0y
2
z
⇒ Circunferencia
=+
=
222
Rzx
0y
Traza sobre el plano YZ:
T
YZ
:
=++
=
222
Ryx
0x
2
z
⇒ Circunferencia
=+
=
222
Ry
0x
z
III) Simetrías
( ) ( ) ( )
22222
222
RzyxRzyx =++⇒=−+−+−
225
Toda superficie esférica con centro en el origen de coordenadas es simé-
trica respecto de los tres planos coordenados, respecto de los tres ejes
coordenados y respecto del origen.
IV) Intersección con planos paralelos a los planos coordenados. Exten-
sión.
Intersección con planos paralelos al plano XY:
=
=++
kz
Rzyx
2222
2222
Rkyx =++
2222
kRyx −=+
La intersec-
ción es:
( ) ( )
nariancia imagicircunfereuna Es
RkóRksisea,o0kRSic)
R0,0,óR0,0,punto un Es
Rksisea,o0kRSi b)
nciacircunfereuna es
RkRsisea,o0kRSia)
22
22
22
>−<<−
−
±==−
<<−>−
Intersección con planos paralelos al plano XZ:
=
=++
ky
Rzyx
2222
2222
Rzkx =++
2222
kRx −=+ z
226
La intersec-
ción es
( ) ( )
nariancia imagicircunfereuna Es
RkóRksisea,o0kRSic)
0R,0,ó0R,0,:punto un Es
Rksisea,o0kRSi b)
nciacircunfereuna es
RkRsisea,o0kRSia)
22
22
22
>−<<−
−
±==−
<<−>−
Intersección con planos paralelos al plano YZ:
=
=++
kx
Rzyx
2222
2222
Rzyk =++
2222
kRzy −=+
La intersec-
ción es
( ) ( )
nariancia imagicircunfereuna Es
RkóRksisea,o0kRSic)
00,R,ó00,R,:punto un Es
Rksisea,o0kRSi b)
nciacircunfereuna es
RkRsisea,o0kRSia)
22
22
22
>−<<−
−
±==−
<<−>−
227
V) ¿Es superficie de revolución?
La superficie esférica es una superficie de revolución porque se puede
generar por la rotación de una circunferencia alrededor de uno de sus
diámetros
VI) ¿Es superficie reglada?
La superficie esférica no es superficie reglada ya que su ecuación no pue-
de descomponerse en el producto de ecuaciones de primer grado.
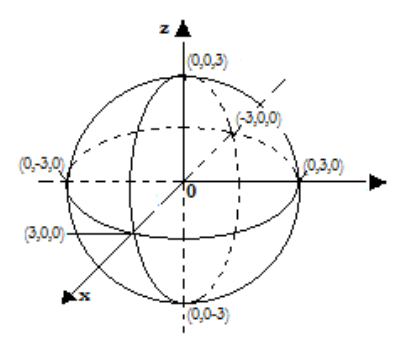
Ejemplo: Analizar y representar (Fig. 8.11.) la superficie esférica
x
2
+ y
2
+ z
2
= 9
Fig.8.11.
Este documento contiene más páginas...
Descargar Completo
Capitulo 15 Superficies cilíndricas y cónicas..pdf
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
Estamos procesando este archivo...
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.