Pág. 1
Capítulo 1
Vectores en R
n
1.1.- Introducción
La geometría euclídea y el álgebra renacentista estaban predestinadas a entenderse y
fusionarse, de hecho, lo hicieron por medio de la obra de Descartes (1596 – 1650) y
Fermat (1601 – 1665) en una nueva geometría que se denominó Geometría Analítica. El
alcance de esta geometría se vio reforzado por la aparición del cálculo infinitesimal, que
se aplicó al estudio de los problemas geométricos.
En el siglo XVII y XVIII el dominio de los métodos analíticos en las matemáticas era tal
que la geometría euclídea se estudiaba olvidándose del rigor euclídeo y colocando en su
lugar ecuaciones que representaban curvas, pares de números que representaban puntos
y utilizando métodos de resolución de ecuaciones al principio y del cálculo infinitesimal
después, como metodología de resolución de problemas geométricos.
A finales del siglo XVIII había unos pocos matemáticos que permanecían ligados al uso
exclusivo de métodos denominados tradicionalmente geométricos, la gran mayoría
utilizaba los métodos algebraicos enriquecidos por los métodos infinitesimales.
Del último grupo es William K. Clifford (1845 – 1879) el primero en dar una formulación
moderna de la definición de los vectores, sus operaciones y los productos escalar y
vectorial en su obra Elementos de Dinámica. Más precisamente los métodos vectoriales
se impusieron en la geometría entre 1830 y 1880.
En la actualidad, no solo partes de las matemáticas como: álgebra lineal, geometría
analítica, cálculo avanzado, sino también la teoría electromagnética, el análisis vectorial,
entre otras, utilizan vectores a la hora de entender el proceso de matematización de
algunos fenómenos de la naturaleza.
Variables físicas que tienen magnitud, dirección y sentido se representan
matemáticamente con vectores. La posición, velocidad y aceleración de una partícula son
vectores, así como las fuerzas.
De este modo, es de gran importancia el estudio de la Geometría Analítica y
particularmente del tema vectores, más aún si está destinado para estudiantes de
ingeniería.
En este primer capítulo estudiaremos los conceptos más importantes de vectores en
y ejemplificaremos en la gran mayoría de los casos para
.
Pág. 2
Luego de ver la definición formal, igualdad y vector posición de un punto, se realizará el
estudio de las operaciones más comunes entre vectores: suma, producto por un escalar
y resta.
En el apartado Otras operaciones con vectores, se presentará uno de los tres productos
entre vectores, el producto escalar y los diversos conceptos que esta operación permite
establecer entre vectores (perpendicularidad, módulo, ángulo, etc.).
Finalmente se hace un estudio detallado del producto vectorial y mixto entre vectores.
Enfatizando que en la mayoría de las operaciones se destaca tanto las aplicaciones en
física, como su interpretación geométrica.
1.2.- Conceptos básicos
El ser humano siempre se preocupó por cuantificar las cosas, es decir, asignar un valor
cuantitativo o cualitativo a las cosas. Por ejemplo, podemos medir de manera precisa, la
distancia entre dos puntos, el peso de un insecto, la temperatura actual en una
habitación, etc. De igual manera podemos medir, pero de forma menos precisa y más
subjetivamente, la belleza de un cuadro artístico, el sabor de una comida.
Una magnitud es toda cualidad relativa a un proceso natural o un cuerpo que puede
medirse, y consecuentemente, expresarse con un valor numérico.
Las magnitudes que pueden definirse mediante un número y las unidades utilizadas para
su medida, se denominan magnitudes escalares; en cambio, si además se debe especificar
dirección y sentido, a esas magnitudes se las llama vectoriales.
Con esta diferencia intuitiva veamos la definición de vector y sus operaciones básicas.
Vector de
: Llamaremos n–vector a una n–tupla ordenada de n números reales, así
Los elementos de
se suelen denotar como
, en donde
es la primera
componente,
la segunda componente y en general
la i–ésima componente.
Cualquier vector de
cuyas componentes sean cero se denomina vector nulo y lo
denotamos como
.
Ejemplo 1:
es un vector de
cuya primera y segunda componente son –1 y
2 respectivamente; en cambio
es un vector de
cuya primera, segunda,
tercera y cuarta componente son 1, 2, –5 y 0 respectivamente.
Ejemplo 2: los vectores
son vectores de
y se los llama vectores canónicos. Vale decir, un vector canónico de
es aquel en
donde solo una componente vale 1 y todas las demás, cero.
Geométricamente, un n–vector
es un segmento de recta orientado que
tiene por punto inicial el origen y extremo el punto
. Por lo

Pág. 3
tanto los elementos de
pueden pensarse como puntos o vectores geométricos de
acuerdo a lo que se requiera en el contexto de trabajo.
Dado un segmento de recta orientado (vector geométrico) con punto inicial
y punto final
existe un n–vector
con la misma longitud y dirección que
: basta tomar
. En consecuencia:
A cada n–vector es posible asociarle un segmento de recta orientado y, recíprocamente, a
cada segmento de recta orientado se le puede asociar un n–vector con la misma longitud y
dirección, pero con punto inicial en el origen.
Vector posición de un punto: Sea el punto
. El punto P determina con el
origen de coordenadas un vector
que llamaremos vector posición del punto P.
Ejemplo 1: en
el punto tiene por vector posición
Gráfico 1
Ejemplo 2: en
el punto tiene por vector posición
Gráfico 2
Igualdad de vectores: Sean
vectores de
se dice
que son iguales si y solo si tienen todas las componentes correspondientes, iguales.
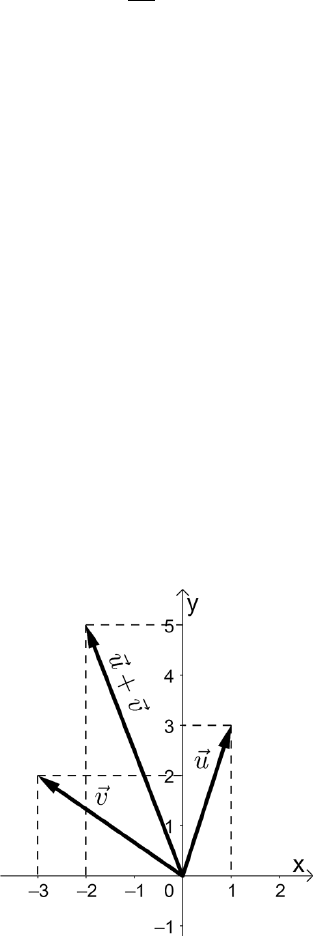
Pág. 4
Sean
Ejemplo 1: para que los vectores de
sean iguales, debe ser
por razones similares no es igual a .
Ejemplo 2: determinar para los cuales son iguales los siguientes vectores de
.
Verificación: si
.
2.- Operaciones con vectores
Dadas unas cantidades vectoriales, es posible obtener otras a partir de ellas si hacemos
uso de las operaciones básicas entre vectores: la suma y la multiplicación por escalares
que definiremos a continuación.
2.1.- Suma de vectores: La suma de dos vectores,
es otro vector,
, cuyas componentes son la suma de las respectivas
componentes de los vectores
.
Sean
.
Ejemplo 1: sean los vectores de
.
Gráfico 3
Ejemplo 2: sean los vectores de
al realizar su suma
obtendremos:
. Esto se muestra en el gráfico 4.
Ejemplo 3: sean los vectores de
al realizar su
suma obtendremos:
.

Pág. 5
Gráfico 4
Gráficamente la suma en
se puede realizar mediante la regla del paralelogramo, que
consiste en construir un paralelogramo que tenga por lados los dos vectores dados. La
diagonal (vector) del paralelogramo, que tiene por origen el origen de coordenadas,
representa la suma de los vectores.
El siguiente gráfico, muestra la suma del Ejemplo 1.
Gráfico 5
2.2.- Producto por un escalar: El producto de un vector
por un
escalar , es el vector
cuyas componentes son el producto del escalar por las
respectivas componentes del vector dado.
Sea
.

Pág. 6
Ejemplo: sea el vector
y el escalar entonces
.
En términos geométricos, el vector
es el vector que tiene igual dirección (recta que
contiene al vector) que
y que dependiendo del signo de tiene igual sentido
o
sentido opuesto
al del vector
y cuya longitud es igual al valor absoluto de por
la longitud del vector
.
Ejemplo 1: sea el vector
, entonces el vector
tendrá la
misma dirección y sentido que
, y una longitud igual al triple de la de
.
Gráfico 6
Ejemplo 2: sea el vector
, entonces el vector
tendrá la misma dirección y sentido opuesto que los de
, y una longitud igual a la mitad
de la de
.
Gráfico 7
De acuerdo a la definición del producto de un vector por un escalar, si el vector es
y el escalar es:
a) , entonces
vector opuesto a
.
b) entonces
vector nulo.

Pág. 7
Aplicación del producto de un vector por un escalar: la Segunda Ley de Newton (Ley
Fundamental de la Dinámica) relaciona el concepto de aceleración con la fuerza. Si una
fuerza neta que actúa sobre un cuerpo hace que éste acelere en la misma dirección que
la fuerza neta, la magnitud de la aceleración es directamente proporcional a la magnitud
de la fuerza neta que actúa sobre él, siendo sus direcciones y sentidos iguales. Esta ley
puede enunciarse de la siguiente manera:
Si una fuerza
1
neta no nula
actúa sobre un cuerpo, este cuerpo se acelera
. El
vector aceleración tiene la misma dirección y sentido que la fuerza neta o resultante y es
inversamente proporcional a la masa del cuerpo:
donde m es la masa del cuerpo,
siendo una magnitud escalar.
Esta relación también puede escribirse en su forma más conocida:
(1).
La ecuación (1) nos indica dos cuestiones:
a) Al ser la masa la medida de la inercia del cuerpo, es un escalar, por lo tanto en la
segunda Ley de Newton se aplica la operación producto de un vector
por un escalar
(m) y se obtiene otro vector
.
b) Los vectores fuerza neta (o resultante) y aceleración son paralelos
2
, ya que uno se
obtiene a partir del otro multiplicado por un escalar.
Propiedades de la suma de vectores y producto por un escalar
Veremos a continuación, cuáles son las propiedades algebraicas que poseen las dos
operaciones básicas antes definidas, estas propiedades son similares a las que poseen
las operaciones de suma y producto de números reales.
P
1
) La suma es ley de composición interna en
.
Esto significa que la suma, como está definida, es una operación que a cada par de
elementos de
le hace corresponder un único elemento de
.
D) Es inmediata por la definición de suma en
.
P
2
) La suma es asociativa en
.
D) Sean
las i–ésimas componentes de los vectores
respectivamente. Por lo
tanto
es la i–ésima componente de
, así que
es la i–ésima
componente de
. Como
por la
1
Fuerza es una magnitud vectorial que se puede simbolizar como
2
Ver el apartado “Vectores paralelos”
Pág. 8
propiedad asociativa de números reales, las componentes respectivas de
y de
son iguales. Concluimos entonces que
.
P
3
) La suma es conmutativa en
.
.
D) Sean
las i–ésimas componentes de los vectores
respectivamente. Por lo tanto
es la i–ésima componente de
. Como
por la
propiedad conmutativa de números reales, las componentes respectivas de
y de
son iguales. Concluimos entonces que
.
P
4
) Existe un único elemento neutro para la suma en
.
El elemento neutro se denota con
.
.
D) La existencia es evidente puesto que se definió el vector nulo como aquel vector cuyas
componentes son cero.
Para demostrar la unicidad del neutro vamos a suponer que existen dos neutros para la
suma:
, por lo tanto, si:
es neutro entonces
es neutro entonces
De donde se deduce, por ser los primeros miembros de ambas igualdades iguales, que
y consecuentemente el neutro es único.
P
5
) Todo elemento en
admite un único inverso aditivo u opuesto en
.
El elemento opuesto a uno cualquiera
, se nota por –
.
.
La existencia de tal vector es evidente puesto que cuando se definió producto por un
escalar, si el escalar es –1 al multiplicarse por cualquier vector se obtiene el opuesto de
dicho vector.
Para demostrar la unicidad del elemento opuesto vamos a suponer que para un elemento
existen dos opuestos
por lo tanto se debe cumplir que
y
también que
de donde se deduce que
. Consecuentemente el inverso
aditivo u opuesto de cada elemento de
es único.
P
6
) El producto es ley de composición externa en
con escalares en .
.
Esto significa que el producto de un vector de
por un escalar, como está definido, es
una operación que a cada par vector–escalar, le hace corresponder un único elemento de
.
Pág. 9
D) La existencia de tal vector es inmediata, por la definición de producto de un vector de
por un escalar.
P
7
) El producto por un escalar satisface la asociatividad mixta.
.
D) Sea
la i–ésima componente del vector
. Por lo tanto
es la i–ésima componente
de
y por lo tanto
la i–ésima componente de
. Como
por la propiedad asociativa del producto de números reales, las componentes
respectivas de
y de
son iguales. Concluimos entonces que
.
P
8
) El producto por un escalar es distributivo respecto a la suma en .
.
D) Sea
la i–ésima componente del vector
. Por lo tanto
es la i–ésima
componente de
. Como
por la propiedad
distributiva del producto de números reales, respecto a la suma, las componentes
respectivas de
y de
son iguales. Entonces, por igualdad de vectores, se
concluye:
.
P
9
) El producto por un escalar es distributivo respecto a la suma en
.
.
D) Sean
las i–ésimas componentes de los vectores
respectivamente. Por lo tanto
es la i–ésima componente de
, como también
es la i–ésima
componente de
. Como
por la propiedad
distributiva del producto de números reales, respecto a la suma, las componentes
respectivas de
y de
son iguales. Concluimos entonces que
.
P
10
) La unidad para los es el neutro para el producto por un escalar.
.
El conjunto de vectores de
entre los cuales se definieron las operaciones de suma y
producto por un escalar con las respectivas propiedades, determinan un espacio vectorial
y constituyen una estructura de las más importantes en matemática.
La importancia de esta definición axiomática es que amplía la idea geométrica intuitiva
de vector. Cualquier conjunto de elementos entre los cuales pueda definirse las
operaciones anteriores y que cumplan con las mismas propiedades podrá considerarse
como un espacio vectorial y sus elementos como vectores, aunque a veces pueda resultar
difícil interpretarlos como segmentos orientados.

Pág. 10
2.3.- Resta de vectores: La resta de dos vectores,
es otro vector,
, que se obtiene sumando al vector minuendo el
opuesto del vector sustraendo, es decir,
.
Sean
.
Geométricamente el vector opuesto a uno dado, es aquel que tiene la misma dirección y
longitud, pero sentido contrario.
Ejemplo 1: sean los vectores de
.
Gráfico 8
Geométricamente, se puede interpretar que la resta
es la diagonal del
paralelogramo de lados
que va desde el punto final de vector
hasta el punto final
del vector
.
Gráfico 9
Ejemplo 2: sean los vectores de
. Esto
se muestra en el gráfico 10.

Pág. 11
Gráfico 11a
2.4.- Vector determinado por dos puntos de
: Las componentes de un vector
determinado por dos puntos P y Q de
son iguales a las diferencias entre las coordenadas
respectivas del punto Q (punto extremo) y P (punto origen). Es decir:
siendo
el vector posición del punto Q y P respectivamente.
Si
Gráfico 10
Ejemplo 1:
Sean los puntos y , cuyos vectores posición son
.
.
Debemos tener en cuenta que
ya que
mientras que
.
Gráfico 11b

Pág. 12
Ejemplo 2:
Sean los puntos P y Q, cuyos vectores posición son
. Esto se muestra en el gráfico 12.
En
ocurre exactamente lo mismo que en
respecto a los vectores
.
3.- Vectores paralelos: Dos vectores no nulos
se dicen paralelos si existe tal que
.
Gráfico 12
La definición de vectores paralelos nos indica que dos vectores no nulos son paralelos si
uno se puede obtener a partir del otro, multiplicado por un escalar.
Ejemplo1: los vectores
de
son paralelo ya que
.

Pág. 13
Gráfico 13
Veamos una característica importante de los vectores paralelos, que se deduce a partir
de la definición.
Por lo tanto
Esto significa que la condición necesaria y suficiente para que dos vectores sean paralelos
es que sus componentes homologas sean proporcionales.
Si el valor de la constante de proporcionalidad es positivo, los vectores tienen el mismo
sentido y si es negativo tienen sentido opuesto.
Ejemplo 2: los vectores
de
son paralelos y de sentidos
opuestos ya que
.
Gráfico 14
4.- Otras operaciones con vectores
Se mencionó que una de las características de un vector es la longitud que tiene este,
concepto que intuitivamente entendemos pero que deberíamos formalizar. Para este
efecto, estudiaremos otra operación: el producto escalar entre dos vectores, la cual se

Pág. 14
relaciona directamente con el concepto de longitud de un vector y la noción de ángulo
entre vectores.
Cabe mencionar que el producto escalar no es el único producto que se realiza entre
vectores, también existen el producto vectorial y el producto mixto.
4.1.- Producto escalar
3
: Dados dos vectores,
definimos producto escalar,
, como el escalar que se obtiene al sumar los producto de
las componente de
con las respectivas componentes de
Dados
ó
escrito de manera resumida
Ejemplo: dados los vectores
calcular
los siguientes productos escalares:
.
.
.
evidentemente no está definido ya que son vectores de distintos espacios.
Al ser el producto escalar una nueva operación entre vectores cuyo resultado es un
número real, nos podemos preguntar ¿Cuáles de las propiedades del producto entre
números reales se satisfacen para el producto escalar entre vectores?
Propiedades del producto escalar
P
1
) El producto escalar es conmutativo
D) Sean
las i–ésimas componentes de los vectores
respectivamente. Por lo tanto
es el i–ésimo término de
. Como
por la propiedad
conmutativa de números reales, los términos respectivos de
y de
son iguales.
Concluimos entonces que
P
2
) El producto escalar no es asociativo
D) Para comprobar que esto es verdad, razonamos de la siguiente manera. Al realizar el
producto escalar
obtenemos un escalar , que al multiplicar al vector
da por
resultado un vector en la misma dirección que este último, mientras que al hacer el
producto escalar
se obtiene un escalar, , que al multiplicar al vector
da por
resultado un vector en la misma dirección que este último. Por lo tanto, los vectores que
se obtienen en ambos miembros no necesariamente tienen las mismas direcciones,
quedando así comprobado que el producto escalar no es asociativo.
3
Esta operación también suele llamarse producto punto ó producto interno.
Pág. 15
El razonamiento anterior se puede resumir esquemáticamente de la siguiente manera:
P
3
) El producto escalar es distributivo respecto a la suma de vectores
D) Sean
las i–ésimas componentes de los vectores
respectivamente. Por lo
tanto
es la i–ésima componente de
, también
será el i–ésimo término
de
. Como
por la propiedad distributiva
del producto de números reales, respecto a la suma, los términos respectivos de
y de
son iguales. Concluimos entonces que
Para la segunda parte de la propiedad se razona de manera similar.
P
4
) El producto escalar es asociativo respecto al producto por un número real
D) Sean
las i–ésimas componentes de los vectores
respectivamente. Por lo tanto
es el i–ésimo término de
. Como
por la propiedad
conmutativa del producto de números reales, los términos respectivos de
y de
son iguales. Concluimos que
Para la segunda parte de la propiedad se razona de manera similar.
P
5
) El producto escalar de un vector por sí mismo es un número real mayor o igual que
cero
D) Sea
, entonces:
y la suma de cuadrados siempre es
positiva o cero.
P
6
) El producto escalar de un vector por sí mismo es cero si y sólo si el vector es nulo.
. De donde se puede concluir que
Sabemos que si el producto de dos números reales e es cero, necesariamente es ó
cero. Esto no ocurre con el producto escalar de vectores, como lo muestra el siguiente
ejemplo.
Sean los vectores
entonces
Este documento contiene más páginas...
Descargar Completo
Capitulo 15 Superficies cilíndricas y cónicas..pdf
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.