
1
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
FACULTAD REGIONAL CÓRDOBA
ÁLGEBRA Y GEOMETRÍA
ANÁLITICA
TEÓRICO
AÑO 2022
Ing CLAUDIO BERASATEGUI

2
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
Este apunte tiene como referencia el Apunte de Álgebra y Geometría Analítica confeccionado en el año 2010
por los Ingenieros Manuel Muñoz y Jorge Bobone, como un apoyo de la parte Teórica para los alumnos que
cursaban las Carreras de Ingeniería en la UTN FRC. En ese momento también se editaba un pequeño apunte
preparado por el Ing Oscar Coraglio sobre Algebra Lineal que era un resumen de temas tomados del libro
Introducción al Algebra Lineal de Howard Anton
1. Competencias
"Las asignaturas homogéneas pertenecientes al Bloque de las Ciencias Básicas de la Ingeniería,
aportan a las Competencias Genéricas sociales políticas y actitudinales y especialmente a las
Tecnológicas. Este aporte se realiza mediante modelos que gradualmente promueven el desarrollo de
las Competencias Específicas necesarias para proyectar, diseñar y calcular"
2. Objetivos de la materia
Desarrollar las capacidades de abstracción, generalización y particularización, fortaleciendo el
pensamiento deductivo e inductivo mediante el uso de operaciones y propiedades de los objetos
matemáticos en problemas de aplicación.
Resolver problemas de aplicación modelizados matemáticamente con la utilización de vectores y
matrices, interpretando los resultados obtenidos en el contexto de la situación, identificando sus
elementos, usando distintas representaciones semióticas y comunicándolos mediante lenguaje
matemático apropiado.
Conocer y adquirir destreza en el Álgebra matricial y sus aplicaciones.
Aplicar los fundamentos de los sistemas de ecuaciones lineales para resolver situaciones
problemáticas, analizándolas mediante argumentos teóricos, empleando técnicas, procesos analíticos
y representaciones gráficas.
Resolver problemas de aplicación utilizando elementos de geometría analítica, interpretando los
resultados obtenidos en el contexto de la situación, identificando sus elementos y comunicándolos
mediante lenguaje matemático apropiado.
Gestionar su propio aprendizaje para contribuir al desarrollo de su autonomía, analizando la
bibliografía y páginas de Internet, empleando materiales propuestos por la cátedra y por los estudiantes,
elaborando una producción escrita u oral, auto evaluándose y evaluando constructivamente a sus pares.
Utilizar TIC’s para resolver situaciones problemáticas o ejercitación confrontando lo obtenido en la
computadora con el resultado esperado e interpretando las respuestas con fundamentos teóricos.
Familiarizarse con los conceptos básicos del Álgebra Lineal: Espacios Vectoriales, Aplicaciones
lineales, Valores y Vectores Propios, en vista de la ulterior comprensión de sus diversas aplicaciones.
3. Evaluación
3.1- Modalidad Cuatrimestral
Parciales Prácticos: Se efectuarán 2 (dos) Evaluaciones parciales prácticas obligatorias individuales.
Se aprobarán con nota igual o superior a 6 (seis) puntos. Se podrá recuperar 1 (uno) de los parciales,
ya sea por nota menor a 6 (seis) o por ausentismo, debiendo resolver un grupo de ejercicios de carácter
práctico y de aplicación a la Ingeniería.
Parciales teóricos: Se efectuarán 2 (dos) Evaluaciones parciales teóricos no obligatorias individuales.
Se aprobará con nota igual o superior a 7 (siete) puntos. Se podrá recuperar 1 (uno) de los parciales, ya
sea por nota menor a 7 (siete) o por ausentismo, debiendo responder un grupo de preguntas teóricas y
de aplicación a la Ingeniería.

3
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
3.2- Modalidad Anual
Parciales Prácticos: Se efectuarán 3 (tres) Evaluaciones parciales prácticas obligatorios individuales.
Se aprobarán con nota igual o superior a 6 (seis) puntos. Se podrá recuperar 1 (uno) de los parciales,
ya sea, por nota menor a 6 (seis) o por ausentismo, debiendo resolver un grupo de ejercicios de carácter
práctico y de aplicación a la Ingeniería.
Parciales teóricos: Se efectuarán 3 (tres) Evaluaciones parciales teóricas no obligatorias individuales.
Se aprobarán con nota igual o superior a 7 (siete) puntos. Se podrá recuperar 1 (uno) de los parciales,
ya sea por nota menor a 7 (siete) o por ausentismo, debiendo responder un grupo de preguntas teóricas
y de aplicación a la Ingeniería. Tendrá una duración de 1 (una) hora.
4. Condiciones de la materia
Abandono: en el caso que un estudiante no rindiera ninguno de los parciales prácticos mencionados
en el punto anterior, el docente responsable deberá cargar esta condición en el sistema académico,
quedando el estudiante en dicha situación.
Libre: si un estudiante aprobara sólo 1 (uno) de los parciales prácticos, el docente responsable deberá
cargar esta condición en el sistema académico, quedando el estudiante en dicha situación.
Regular: si un estudiante aprobara 2 (dos) parciales prácticos, en la modalidad cuatrimestral, o 3 (tres)
parciales en la modalidad anual, con nota de 6 (seis) o más, incluyendo las instancias recuperatorias
correspondientes, el docente responsable deberá cargar esta condición en el sistema académico,
debiendo el estudiante en el examen final, rendir la parte práctica de la materia y, de aprobar, rendirá
la parte teórica, con un tribunal a designar por la cátedra.
Aprobación completa: si un estudiante aprobara 2 (dos) parciales prácticos con nota 7 (siete) o
superior, en la modalidad cuatrimestral, o 3 (tres) parciales en la modalidad anual, y además aprueba
2 (dos) parciales teóricos, en la modalidad cuatrimestral, o 3 (tres) parciales en la modalidad anual,
incluyendo las instancias recuperatorias correspondientes, el docente responsable deberá cargar esta
condición en el sistema académico, completando la última columna de nota final con el promedio de
las notas alcanzadas en los exámenes teóricos, debiendo el estudiante en examen final, sólo anotarse
para rendir, teniendo como nota de examen, la misma que el profesor responsable ha cargado en la
columna correspondiente
5. Evaluación final
Condición regular: el estudiante deberá rendir un examen práctico virtual, por la UV, por la mañana,
de aprobar ese examen, por la tarde, deberá rendir un examen presencial práctico/teórico en las
instalaciones del UTN, con un tribunal propuesto por la Cátedra.

4
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
PROGRAMA ANALÍTICO
UNIDAD N°1: Vectores libres en
2
y
3
.
Vectores libres. Definición. Operaciones de “suma” y “multiplicación por un escalar”. Propiedades.
Paralelismo de vectores libres. Expresión cartesiana de un vector.
Producto escalar canónico en
2
y
3
. Definición y propiedades.
Aplicaciones del producto: Longitud de un vector. Ángulo entre vectores.
Ortogonalidad. Vectores unitarios. Descomposición de un vector en dos direcciones perpendiculares.
Distancia entre dos puntos.
“Producto vectorial” y “Producto mixto” de vectores en
3
. Definición. Propiedades. Aplicaciones.
UNIDAD N°2: Rectas y planos.
Ecuaciones vectoriales, paramétricas y cartesianas de la recta en
2
y
3
.
Ecuaciones vectoriales, paramétricas y cartesianas del plano en
3
.
Posiciones relativas entre dos rectas, dos planos, una recta y un plano.
Problemas de paralelismo e intersección. Problemas de distancia. Ecuación normal de la recta y el
plano. Ángulo entre dos rectas, ángulo entre rectas y planos. Ángulos entre planos.
Haz de rectas. Haz de planos.
UNIDAD N°3: Cónicas y Cuádricas.
Circunferencia, definición, ecuación canónica, ordinaria y general.
Parábola, definición, ecuación canónica, foco, directriz, ecuación ordinaria y general.
Elipse, definición, ecuación canónica, focos, excentricidad, ecuación ordinaria y general.
Hipérbola, definición, ecuación canónica, focos, excentricidad, asíntotas, ecuación ordinaria y general.
Cuádricas: elipsoide, hiperboloide, paraboloide, etc. Ecuaciones. Gráficos
UNIDAD N°4: Vectores en
n
.
Definición. Operaciones de “suma” y “multiplicación por un escalar”.
Producto escalar canónico en
n
Combinación lineal de vectores. Dependencia e independencia lineal de vectores.
UNIDAD N°5: Matrices.
Matriz, definición, clasificación.
Operaciones de suma de matrices y producto de una matriz por un escalar, propiedades.
Multiplicación de matrices, definición, propiedades.
Operaciones elementales de filas y equivalencias por filas de matrices.
Matriz escalón reducida por filas. Rango de una matriz.
Matrices elementales. Condición de equivalencia de matrices.
Inversibilidad de matrices, definición.
Caracterización de matrices inversibles. Cálculo de la inversa. Método de la matriz reducida por fila.
Inversibilidad de productos y de matices elementales. Propiedades.
UNIDAD N°6: Determinantes.
Definición, propiedades.
Cálculo de determinante. Regla de Sarrus. Desarrollo por cofactores. Método de triangulación.

5
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
Aplicación del determinante a la caracterización de irreversibilidad de una matriz y al cálculo de la
matriz inversa. Método de la matriz adjunta.
UNIDAD N°7: Sistema de ecuaciones lineales.
Sistema de ecuaciones lineales. Notación matricial de un sistema.
Equivalencia de sistemas. Sistemas homogéneos y no homogéneos.
Teorema de Rouche Frobenius.
Métodos de resolución: Gauss, Gauss-Jordan, de la matriz inversa.
Método de Cramer
UNIDAD N°8: Espacios Vectoriales.
Espacios vectoriales y subespacios, definiciones, ejemplos, propiedades.
Definiciones y teoremas de caracterización. Generación de un Espacio Vectorial.
Bases y dimensión de un Espacio Vectorial. Definiciones. Ejemplos. Teoremas.
Cambio de bases. Matriz de cambio de bases.
UNIDAD N°9: Aplicaciones o transformaciones lineales.
Definición. Propiedades. Aplicación lineal matricial.
Imagen y núcleo de una aplicación lineal. Definición. Propiedades. Teoremas de las dimensiones.
Matriz estándar (R
n
→R
m
). Operadores lineales en el plano R
2
→R
2
.
“Composición” de las aplicaciones lineales. Matrices de las transformaciones lineales. Representación
de aplicaciones lineales por matrices. Base canónica y otras bases.
Semejanza y/o similaridad.
UNIDAD N° 10: Valores y vectores propios.
Definiciones de “valor propio”, “vector propio” y “subespacio propio”
Caracterización de los valores propios. Ecuación y polinomio característico.
Determinación de los subespacios propios. Propiedades de los valores y vectores propios.
Operadores diagonalizables.
UNIDAD N°11: Números Complejos.
Operaciones. Suma. Resta. Producto. Cociente.
Formas binómicas

6
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
BIBLIOGRAFÍA
“Introducción al Álgebra Lineal”. H. Antón,
“Álgebra Lineal con aplicaciones”. Stanley Grossman,
“Álgebra Lineal”. S. Lipschutz,
“Álgebra Lineal con aplicaciones”. G. Nakos y D. Joyner,
“Geometría Analítica”. C. Lehmann
“Geometría Analítica del Plano y del Espacio y Nomografía”. D. Di Pietro.
“Nociones de Geometría y Álgebra Lineal”. Kosak, Pastorelli, Vardanega. Editorial Mc Graw
Hill
“Álgebra y Geometría. Teoría, Práctica y Aplicaciones”. S. Gigena, F Molina y otros. Editorial
Universitaria
Álgebra y Geometría Analítica”. A.E. Venturini
Apunte de la Cátedra. Ing Claudio Berasategui

7
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
UNIDAD N°1: Vectores libres en
y
Vectores
Introducción
Abordaremos en este capítulo, el concepto de vector geométrico en los espacios bidimensionales
2
, y
tridimensional
3
, también estudiaremos cómo efectuar operaciones algebraicas entre vectores y sus
propiedades. En la unidad 4 aplicaremos estos conceptos a vectores del espacio
n
.
Objetivos
Esperamos que al finalizar la lectura comprensiva y activa de la presente unidad, pueda:
Identificar una magnitud vectorial.
Sumar y restar, analítica y gráficamente, vectores de
2
y de
3
.
Multiplicar, analítica y gráficamente, un vector de
2
y de
3
por un escalar.
Utilizar las propiedades de las operaciones entre vectores de
2
y de
3
para resolver situaciones
problemáticas.
Expresar vectores en sistemas de coordenadas.
Obtener las coordenadas de un vector relativas a un sistema de referencia.
Describir la dirección de un vector mediante sus ángulos directores.
Obtener el versor asociado a un vector.
Aplicar las formas de cálculo del producto escalar entre vectores, sus propiedades y conceptos
derivados, en la resolución de problemas de Álgebra, Geometría o Física.
Identificar las características del vector que se obtiene de efectuar el producto vectorial entre dos
vectores, reconocer sus propiedades y aplicarlas en la resolución de problemas de Álgebra, geometría
y Física.
Utilizar el producto mixto entre vectores y sus propiedades en la resolución de problemas de Álgebra,
Geometría y Física.
Magnitudes
Escalares
Vectoriales
Quedan determinadas cuando
especificamos su:
Magnitud-Valor numérico
Unidad- utilizada en la medición
Ejemplos
Volumen de un tanque de agua:
100l.
Área de un terreno: 2502
Temperatura corporal: 370°
Quedan determinadas cuando especificamos su:
Módulo-Valor numérico, intensidad de la magnitud
Dirección- es la línea de acción del vector (ref ángulo)
Sentido- es la orientación del vector (punta de flecha)
Ejemplos Dirección
Los autos que se desplazan en una misma calle recta o
en calles paralelas están desplazándose en la misma
dirección.
Una recta vertical.
Ejemplos Sentido
Los autos que se desplazan en una misma calle doble
mano lo pueden hacer en dos sentidos por ejemplo
Este–Oeste u Oeste-Este
En una recta vertical el sentido será hacia arriba o
hacia abajo

8
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
Ejemplo:
Velocidad de un
vehículo
Definición
Un vector es un segmento orientado que se utiliza para representar las magnitudes
vectoriales
Elementos
Recta que determina la dirección
La punta de la flecha indica el sentido
B: extremo
A: origen
α ángulo que indica la dirección
Clases de Vectores
VECTORES
En el cálculo vectorial lo que más interesa son los vectores libres, y las reglas de cálculo son las mismas para
todos los vectores, pero dichos vectores nos permiten realizar operaciones de suma y resta con los métodos
que veremos a continuación, pudiendo realizar representaciones gráficas útiles para el planteo de cálculos; por
ejemplo, en física con los cuerpos en equilibrio. Por esto, prescindiremos en lo que sigue de hacer distinciones
entre ellos y sobreentenderemos que trabajamos con vectores libres.
Suma/Resta de vectores
Para sumar dos vectores y
se procede de la siguiente manera. A partir de un punto cualquiera “O” del
plano se traza un vector equipolente al vector , haciendo coincidir el origen de éste con el punto “O”. Por el
extremo de trazamos un vector equipolente al vector
de tal manera que coincida el origen de éste último
con el extremo de ; y el vector cuyo origen es el origen de y cuyo extremo es el extremo del vector
, es
el vector suma:
Los vectores se indican con letra
minúscula con un guion o Flecha por
encima
El módulo del vector (intensidad de
la magnitud) se indica:
y es número positivo
Aplicados
(fijos)
Tienen el mismo
origen
Equipolentes
Tienen distinto origen
e igual módulo, dirección y sentido
Deslizables o Axiales
Se desplazan sobre la
misma recta de acción
Libres
Se desplazan paralelamente
a su recta de acción
Ejemplo: Peso de
un cuerpo

9
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
Al mismo resultado se llega tomando los vectores y
con el mismo origen “O” y definiendo la suma como
la diagonal que pasa por “O”, del paralelogramo construido con los vectores equipolentes de los vectores y
dados.
O
O
Observando la figura siguiente, deducimos que proyectando la poligonal formada por los vectores ,
y
sobre los ejes coordenados, resulta que las componentes del vector suma
son la suma de las
componentes de los vectores y
.
Dado un vector
se representa por –
al vector opuesto, es decir, al que tiene el mismo módulo y la misma
dirección, pero sentido contrario. Las componentes de
son:
La sustracción o diferencia
de dos vectores es igual a la suma del vector y del vector
, es decir
le sumamos al vector el opuesto del vector
Para la verificación geométrica de la diferencia
procederemos como en el caso de la suma, tomando
en lugar de
.
b
b
b
b
Propiedades
1) Uniforme:
2) Asociativa:
3) Conmutativa:
4) Del cero: existe un único vector, llamado el cero
0
(0, 0) , que sumado con cualquier otro vector no lo
altera:
5) Del opuesto: dado un vector , existe uno opuesto -(es decir el opuesto de un vector es aquel que
tiene las componentes con los signos opuestos o contrarios) que sumado con aquel da por resultado el
vector cero: + (-) =
0
Producto de un vector por un escalar
Propiedades:
1) El producto de un escalar por un vector es distributivo respecto a la suma de escalares:
( λ + σ ) = λ + σ
En efecto, siendo λ y σ de la misma dirección que , su suma nos da un vector de la misma dirección,
cuyo módulo es el valor absoluto de la suma algebraica de dos segmentos cuyo sentido depende de los
signos de λ y σ y cuyos valores absolutos son λ ׀׀ y σ ׀׀.
2) Es distributiva con respecto a la suma de vectores:
λ ( +
b
) = λ + λ
b
3) Goza este producto de la propiedad asociativa respecto del producto de escalares:
λ (σ . ) = (λ.σ) = σ ( λ. )
4) Elemento neutro
Las figuras son análogas al caso de la
suma de vectores. Debemos hacer notar
que la diferencia es la operación inversa
de la suma, es decir:
de donde
se deduce que:
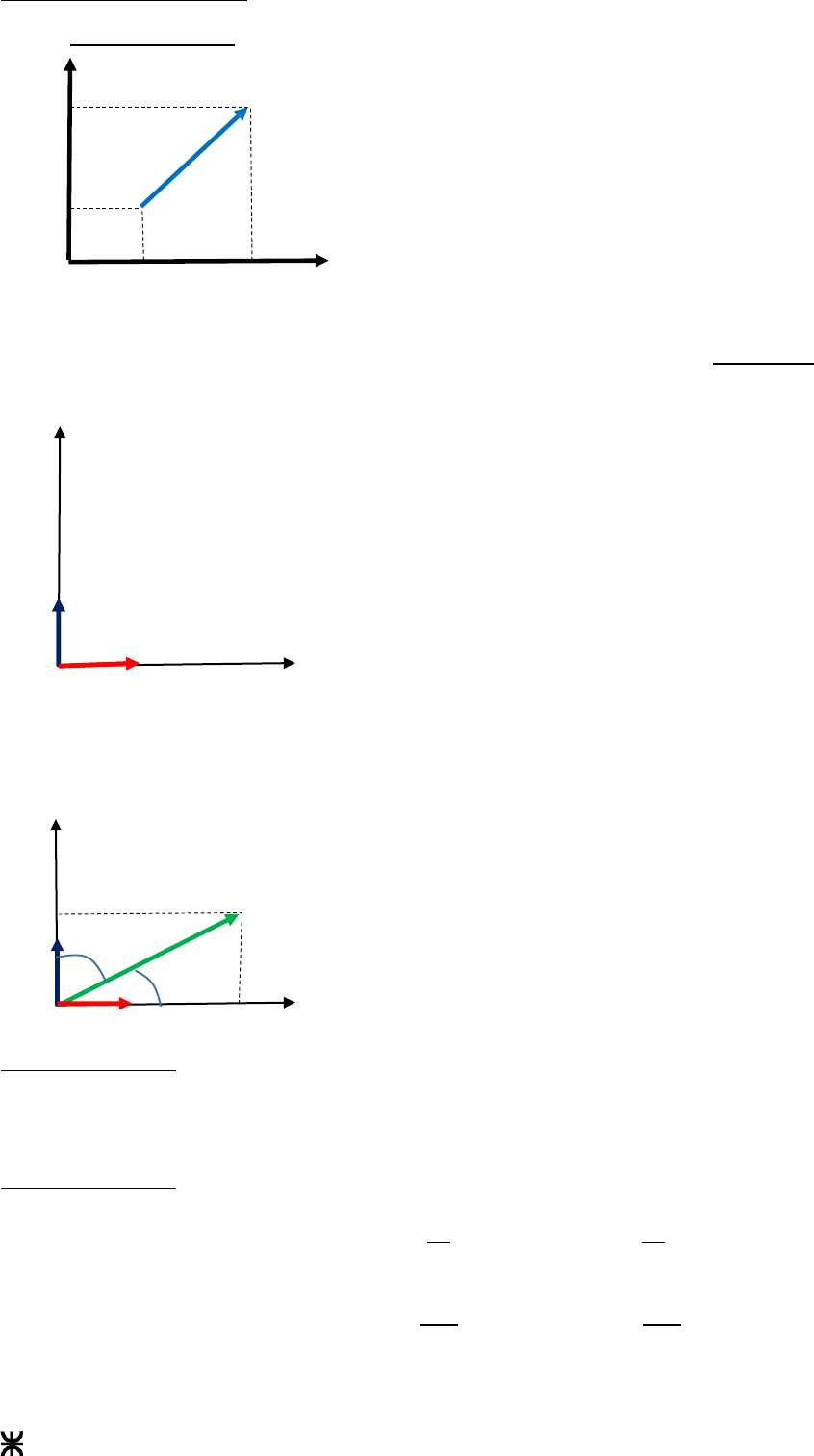
Dado un vector y un escalar λ (o sea un número
real cualquiera), el producto λ . es otro vector de
la misma dirección que , cuyo módulo es igual a λ
veces el módulo de y cuyo sentido es el mismo
de si λ es positivo o el opuesto si λ es negativo.
10
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
y
O
A
B
Componentes de un vector
1- En el plano
Vamos a referir nuestro estudio a un sistema de ejes coordenados
cartesianos ortogonales en el plano bidimensional, de origen “O” y
ejes “x”, “y”.
El origen del vector se encuentra en el punto A de coordenadas
y el extremo en el punto B de coordenadas
.
Si proyectamos el vector, perpendicularmente, sobre los ejes
tendremos las componentes
. Siendo
Para obtener el módulo del vector, aplicaremos Pitágoras, quedando:
Ahora definimos versores, son vectores cuyo módulo es igual a
la unidad, donde tenemos dos versores “especiales” a los que
llamaremos y , dados por:
Donde podemos ver que el versor está sobre el eje x,
pudiéndolo considerar como la unidad vectorial sobre dicho eje,
mientras que el versor se encontrará sobre el eje y, también
considerado como la unidad vectorial sobre el eje y. (ver
gráfico)
Ejemplo:
y son las componentes del vector que sumadas nos dan el vector
y 3 y 2 son las coordenadas de vector.
Es como si quisiéramos explicar dónde vivimos, decimos 3
(coordenada) cuadras (versor ) en la dirección de x, y 2 (coordenada)
cuadras (versor ) en la dirección de y.
Ángulos directores
Un vector forma con los semiejes positivos de los ejes coordenados x e y, ángulos α y β (ver gráfico anterior)
llamados ángulos directores, porque indican la dirección y sentido del vector. Los ángulos son mayores o
iguales a 0° y menores o iguales a 180°.
Cosenos directores
Son los cosenos de los ángulos directores
Gozan de la siguiente propiedad:
Sumando

11
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
La suma de los cuadrados de los cosenos directores es igual a 1
2- En el espacio
Vamos a referir nuestro estudio a un sistema de ejes coordenados cartesianos ortogonales en el espacio
tridimensional, de origen “O” y ejes “x”, “y”, “z”.
z
z
F
a
z
a
z
z
P
F
P a
y
a
x
y
P
a
y
y
F
o y
x
P
a
x
x
F
x
(fig. 1)
Sean P (x
P
, y
P
, z
P
) y F(x
F
, y
F
, z
F
) el origen y el extremo de un vector dado , según lo indicado en la figura.
Se llaman componentes de un vector respecto al sistema de ejes coordenados con origen en 0 y ejes (x, y,
z), a las proyecciones de sobre los ejes, o sea, a los números:
a
x
= x
F
– x
P
; a
y
= y
F
– y
P
; a
z
= z
F
- z
P
(1)
y en forma genérica, escribiremos: (a
x
; a
y
; a
z
) para indicar que a
x
, a
y
, a
z
son las componentes del vector
.
Remarquemos que estas componentes son números que pueden ser positivos o negativos. Siempre debemos
tomarlos como se definen en (1), es decir, como diferencia entre las coordenadas del extremo o del punto final
(F) del vector y las coordenadas del origen o principio del vector (P).
De esta manera resulta que dos vectores opuestos (de igual módulo y de igual dirección, pero de sentidos
opuestos), tienen las componentes iguales en valor absoluto, pero de signos contrarios.
Al observar la figura 1, vemos que el vector es la diagonal de un paralelepípedo, cuyas aristas son: a
x
, a
y
,
a
z
.
El módulo del vector , verifica:
expresión que se toma siempre positiva y que nos da el módulo de un vector en función de sus componentes.

12
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
Ángulos directores
Si hacemos coincidir el origen de un vector , con el origen de un sistema de ejes coordenados ortogonales,
observamos que dicho vector forma con los sentidos positivos de los ejes, los ángulos , y .
z
γ
O
y
x (fig. 2)
Los ángulos hay que tomarlos entre 0º y 180º, de manera que los cosenos directores pueden ser positivos o
negativos.
Cosenos directores
Los cosenos de dichos ángulos se denominan cosenos directores.
De la expresión general del coseno, se deduce:
entonces resulta:
de donde podemos despejar:
que expresan que la proyección de un vector (o segmento orientado) sobre un eje; es igual a la longitud del
segmento (módulo) por el coseno del ángulo que el mismo forma con el eje.
Como en el plano, en el espacio se cumple que:
que es la relación fundamental que liga los cosenos directores de un vector.
De las expresiones (2) y (3), se deduce también que; un vector queda completamente determinado (módulo,
dirección y sentido) por sus componentes.
Igualdad de vectores
Dos vectores se dicen iguales cuando tienen el mismo módulo, la misma dirección y el mismo sentido.
(fig. 3)
Reflexiva
Simétrica
Transitiva
Así los vectores de la figura son iguales, lo cual se escribe:
Esta definición de igualdad es admisible, pues ella cumple las
tres propiedades que se exigen a toda definición de igualdad
entre elementos de un conjunto, a saber:

13
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
El módulo de un vector es siempre un número positivo.
Del análisis y comparación de la definición de componentes de un vector y de la definición general de igualdad
de vectores se deduce: dos vectores iguales tienen las mismas componentes en cualquier sistema de
coordenadas.
Expresión cartesiana ó canónica de un vector
En el plano (2 dimensiones), teníamos dos versores, en el eje “x” tenemos el versor , en el eje “y” el versor
, ahora en el espacio (tenemos 3 dimensiones), debemos sumar el eje “z”, donde tendremos el versor que lo
denominamos
.
Considerando ahora las proyecciones del vector sobre los ejes como vectores; éstos serán: a
x
; a
y
; a
z
,
lo cual resulta de multiplicar los versores por las respectivas componentes del vector
Trasladando los ejes al punto A es fácil ver que el vector resulta como suma geométrica (suma vectorial)
de los vectores proyección:
= a
x
+ a
y
+ a
z
que es la expresión cartesiana del vector.
Entonces en
3
, las componentes de los versores son:
Módulo de un vector
Nuevamente por Pitágoras, nos queda
y despejando, se obtiene finalmente:
Entonces como conclusión tenemos, que el módulo de un vector es igual a la raíz cuadrada de la suma de los
cuadrados de sus componentes.
Vectores paralelos
Si dos vectores (a
x
, a
y
, a
z
) y
(b
x
, b
y
, b
z
) son paralelos y del mismo sentido, tendrán los mismos cosenos
directores y por lo tanto, tendremos:
a
x
=
cos ; a
y
=
cos ; a
z
=
cos γ (1) Paralelos y del mismo
sentido.
b
x
=
cos ; b
y
=
cos ; b
z
=
cos γ (2)
Si son paralelos y de sentidos contrarios, los ángulos que forman con los ejes coordenados difieren en 180º y
por lo tanto, los cosenos directores resultan iguales pero de signos opuestos; o sea que tendremos:
a
x
=
cos
; a
y
=
cos
; a
z
=
cos γ (1) Paralelos y de sentido
contrario.
b
x
=
cos
; b
y
=
cos
; b
z
=
cos γ (3)
De las relaciones entre (1) y (2) y entre (1) y (3), tendremos:

14
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
valiendo el signo más (+) en el primer caso y el signo menos (-) en el segundo.
Como conclusión enunciaremos el siguiente teorema:
La condición necesaria y suficiente para que dos vectores sean paralelos es que sus componentes
homólogas sean proporcionales, es decir:
si el valor de estas igualdades es positivo, los vectores tienen el mismo sentido y si es negativo, tienen
sentidos opuestos.
Producto escalar de dos vectores
Se llama o se define como producto escalar o interno, o producto punto de dos vectores y
, al escalar
obtenido como producto de los módulos de y
por el coseno del ángulo formado por los dos vectores.
Indicaremos el producto escalar con un punto, de manera que será:
siendo θ el ángulo que forman los dos vectores y
sus módulos. Además θ varía entre: 0
0
θ π
Si expresamos los vectores por medio de su forma canónica o cartesiana, tendremos:
y realizando su producto como sí se tratara de dos polinomios (en forma distributiva) y teniendo en cuenta los
productos de los vectores unitarios o versores, tendremos:
Consideremos en la expresión anterior, los productos escalares de los vectores unitarios o versores.
Recordemos que los versores coinciden con los ejes coordenados y estos son perpendiculares entre sí (90º).
Entonces tendremos:
por igual razón:
Recordar que: cos 0º = 1 y que: cos 90º = 0
Analizando ahora los productos cruzados de los versores, tenemos:
y de la misma forma:
Teniendo en cuenta lo aquí analizado, el producto escalar de dos vectores dados en su forma canónica, queda
así determinado:
resultando entonces que el producto escalar de dos vectores dados en su forma canónica no es otra cosa que la
sumatoria de los productos de las componentes homólogas de ambos vectores.
Propiedades:
a) Conmutativo: .
=
.
b) Distributiva respecto a la suma de vectores: . (
+
c
) = .
+ .
c

15
FAC. REG CÓRDOBA Álgebra y Geometría Analítica
c) Si se multiplica uno de los vectores por un número, el producto escalar quedará multiplicado por dicho
número
( λ . ) .
= λ ( .
) = (λ .
) . con la condición de que λ 0
d) . = ׀׀
2
; es decir , ׀׀ = ( . )
½
Demostración de d):
Supuesto que el ángulo θ entre y es cero, se tiene:
(Tener presente que coseno de cero grado es igual a uno → cos 0º = 1)
Aplicaciones del producto escalar
El trabajo W se define como el producto de la intensidad de la fuerza por la longitud del desplazamiento por
el coseno del ángulo comprendido entre la dirección de la fuerza y la dirección del desplazamiento.
Se observa que el trabajo es una magnitud escalar que se obtiene a partir de 2 vectores: un vector fuerza
y
un vector desplazamiento
.
Indudablemente, el trabajo no sólo afecta al módulo de los vectores, sino también a los otros parámetros que
definen un vector, como es el caso de la dirección. De hecho, si la fuerza fuera ejercida en forma perpendicular
a la dirección pretendida del desplazamiento del carro, no se movería, aun incrementando sustancialmente el
valor de la fuerza aplicada, nunca va a conseguir desplazar el carro. El trabajo en esa dirección es 0 (cero), lo
cual muestra que está desperdiciando esfuerzo o, desde otra óptica, que el proceso no está optimizado.
Si se aplica la fuerza en la dirección del desplazamiento, el ángulo comprendido es de 0°, el coseno
correspondiente es 1 (uno), y, por lo tanto, es posible trasladar el carro la misma distancia con menor esfuerzo.
Ángulo de dos vectores
De la definición de producto escalar, se puede considerar que:
, lo que implica que: .
De esta última expresión deducimos que: si es nulo el producto escalar de dos vectores, no siéndolo ninguno
de ellos, podemos asegurar que los vectores son perpendiculares, o dicho de otra manera, la condición
necesaria y suficiente para que dos vectores sean perpendiculares es que su producto escalar sea nulo, no
siéndolo ninguno de los dos vectores
De la expresión del producto escalar .
, se puede despejar el valor de cos θ y a partir de
allí calcular θ , determinando para ello el valor del arc cos , o sea:
pero habíamos visto que:
y también que:
es decir que reemplazando se tiene:
Consideremos el caso de una persona que debe mover un carro
horizontalmente, trasladándolo 20 metros en forma lineal como muestra
la figura.
Realiza el traslado empleando un cable que forma un ángulo de 30° con
la horizontal, y esta dirección coincide con el desplazamiento. Para
mover el carro aplica una fuerza de 20N.
¿Qué trabajo realiza el operario?
Este documento contiene más páginas...
Descargar Completo
Apunte Álgebra y Geomtría Analítica 2022 (1).pdf
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.