Volver a Elementos de Física
Técnicas experimentales de Física General 1/7
Ajuste de una recta por mínimos
cuadrados
• Los datos y su interpretación
• Los parámetros que mejor ajustan.
• Estimación de la incertidumbre de los
parámetros.
• Coeficiente de correlación lineal.
• Presentación de los resultados. Ejemplo.
Técnicas experimentales de Física General 2/7
Los datos y su interpretación
Razones teóricas:
y
mnx=+
N pares de medidas
( , );( , ); ;( , )xy xy x y
NN11 2 2
"
Antes de tomar las medidas:
El intervalo elegido para la variable independiente,
¿abarca todo el rango de interés?
¿Están los puntos uniformemente distribuidos en este
intervalo?
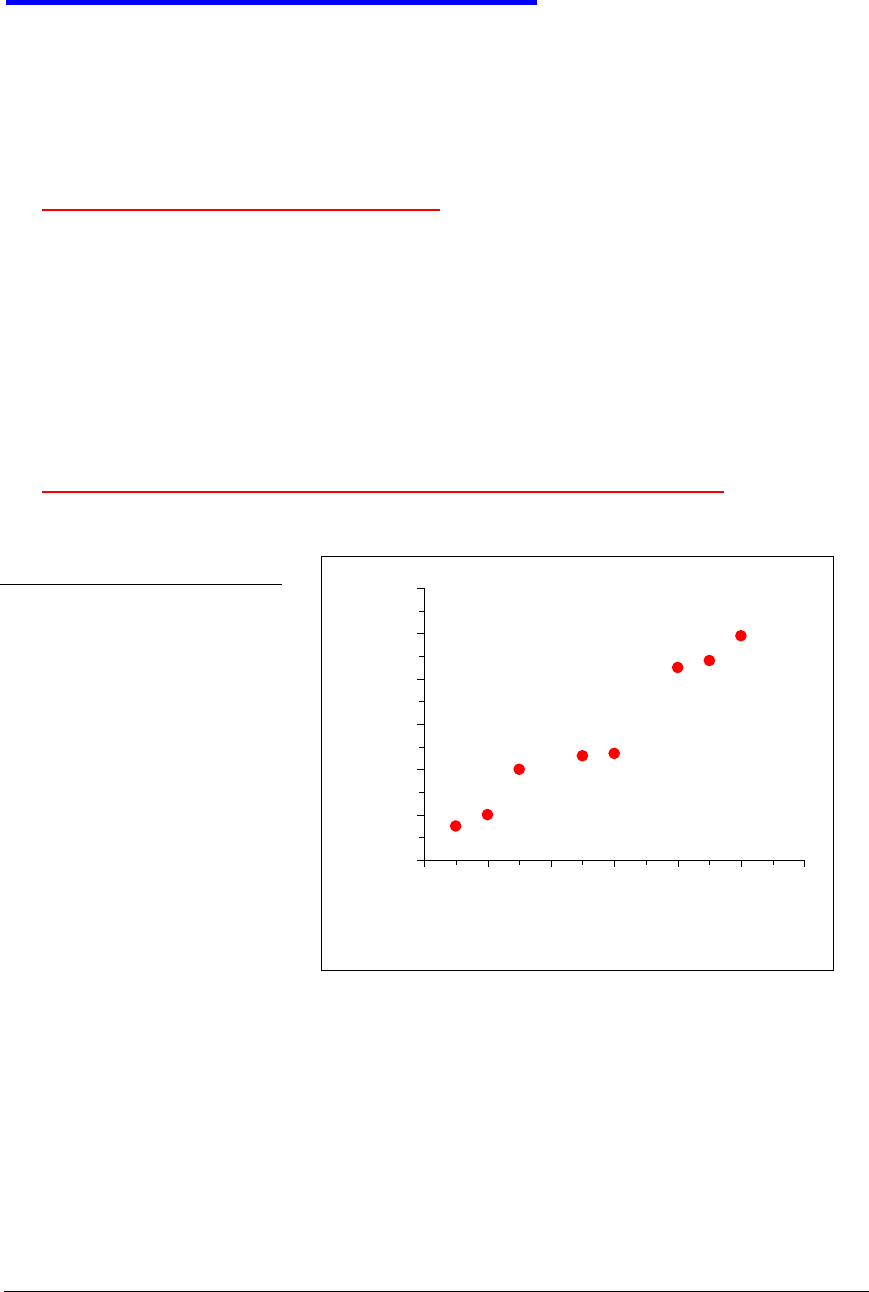
Ordenación y representación gráfica de los datos
x
i
y
i
1 1.5
2 2.0
3 4.0
5 4.6
6 4.7
8 8.5
9 8.8
10 9.9
0
2
4
6
8
10
12
024681012
x(unidades)
y(unidades)
¿Se comportan los pares de medidas visualmente según una línea
recta?
¿Hay algún punto que presente un comportamiento anómalo?
Técnicas experimentales de Física General 3/7
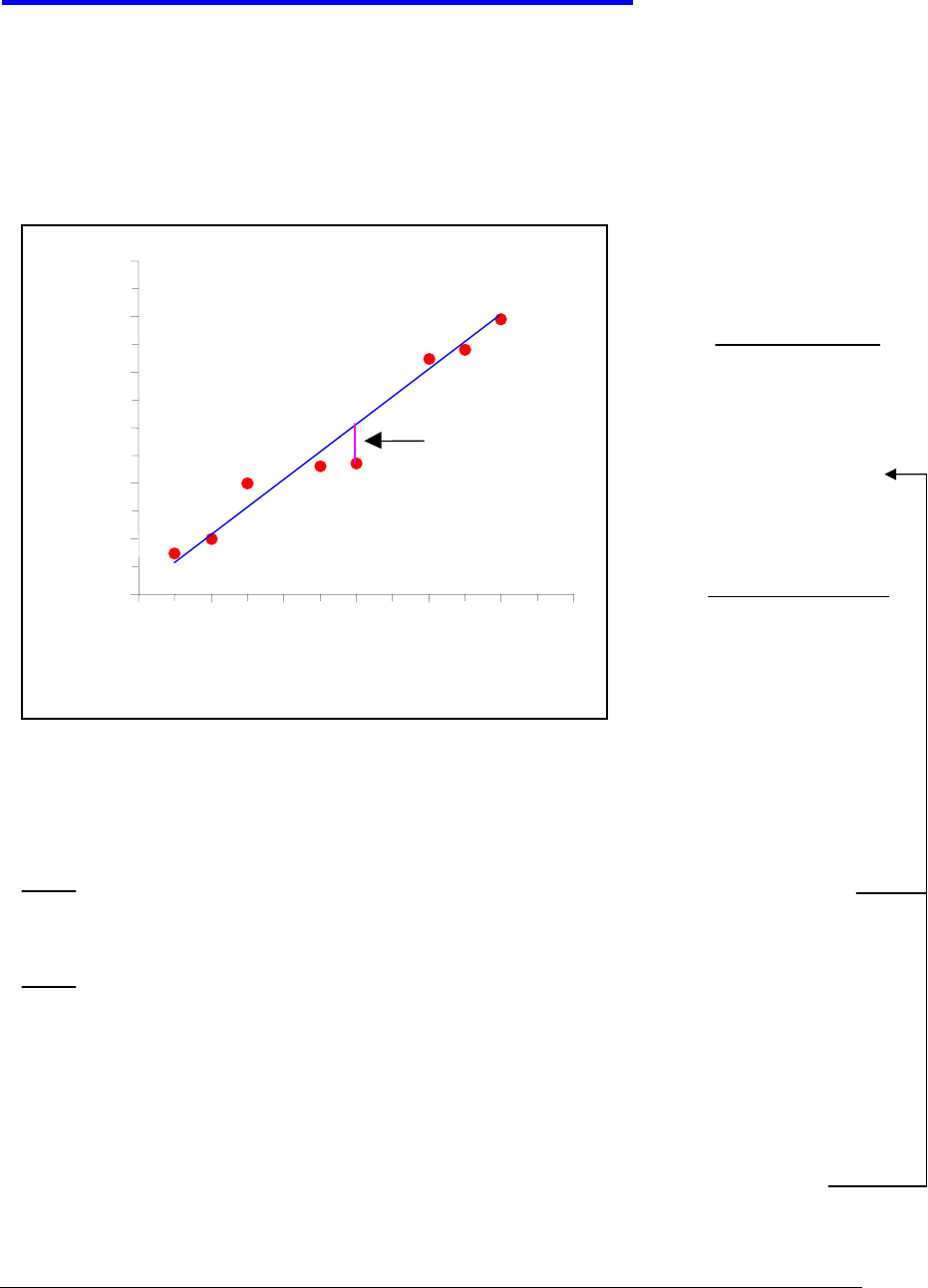
Los parámetros que mejor ajustan
¿Cuál es la recta que mejor se ajusta a las N medidas?
22
1
(, ) ( )
N
ii
i
nm my nx
χ
=
=−−
∑
0
2
4
6
8
10
12
0 2 4 6 8 10 12
X
(
y
(
y
i
-mx
i
-n)
x
yxy
xxx
x
xy xxy
x
xxx
m
n
NS S S
NS S S
SS SS
NS S S
−
=
−
−
=
−
¿Qué valores de m y n hacen mínimo
2
χ
?
()
()
()
2
2
11
2
1
00 2 2
00 2
NN
ii i iiii
ii
N
ii
i
ymxnx yxmx nx
m
ymxn
n
χ
χ
==
=
∂
=→= − − − =− − −
∂
∂
=→= − − −
∂
∑∑
∑
Definiendo
SxSySxSxy
xi
i
N
yi
i
N
xx i
i
N
xy i
i
N
i
== = =
== = =
∑∑ ∑ ∑
11
2
11
Técnicas experimentales de Física General 4/7
Estimación de la incertidumbre de los
parámetros
¿Cuál es el mejor estimador de las incertidumbres de m y
de
n?
Suponemos que:
• Solo los valores y
i
tienen error: δy
i
• Los errores en y son todos iguales: δy
i
= δy =
σ
y
y se
estima a partir de la varianza de los datos:
()
2
),(
2
1
2
2
1
2
−
=−−
−
=
∑
=
N
mn
nmxy
N
N
i
iiy
χ
σ
Aplicando propagación de errores:
2
1
2
∑
=
∂
∂
=
N
j
y
j
m
y
m
σσ
;
2
1
2
∑
=
∂
∂
=
N
j
y
j
n
y
n
σσ
y operando se obtiene:
2
2
2
2
(, )
2
(, )
2
xx
n
xx x x
m
xx x x
S
nm
NS S S N
Nnm
NS S S N
χ
σ
χ
σ
=
−−
=
−−
Técnicas experimentales de Física General 5/7
Coeficiente de correlación lineal
¿Cómo podemos saber cuán bueno es el comportamiento
lineal de los N pares de datos medidos?
Los errores en las medidas
i
y
σ
son conocidos:
• ¿La recta pasa por casi todos las barras de error de los
puntos?
• Test de
2
χ
.
Los errores en las medidas
i
y
σ
son desconocidos:
• A partir de la dispersión de los datos.
• Coeficiente de correlación lineal: r
• Mide el grado de correlación lineal entre x e y.
•
1r ≤
1r =
Correlación total.
0r =
No hay correlación.
r
NS S S
NS S S NS S S
Sy
xy x y
xx x x yy y y
yy i
i
N
=
−
−−
=
=
∑
siendo
2
1
Técnicas experimentales de Física General 6/7
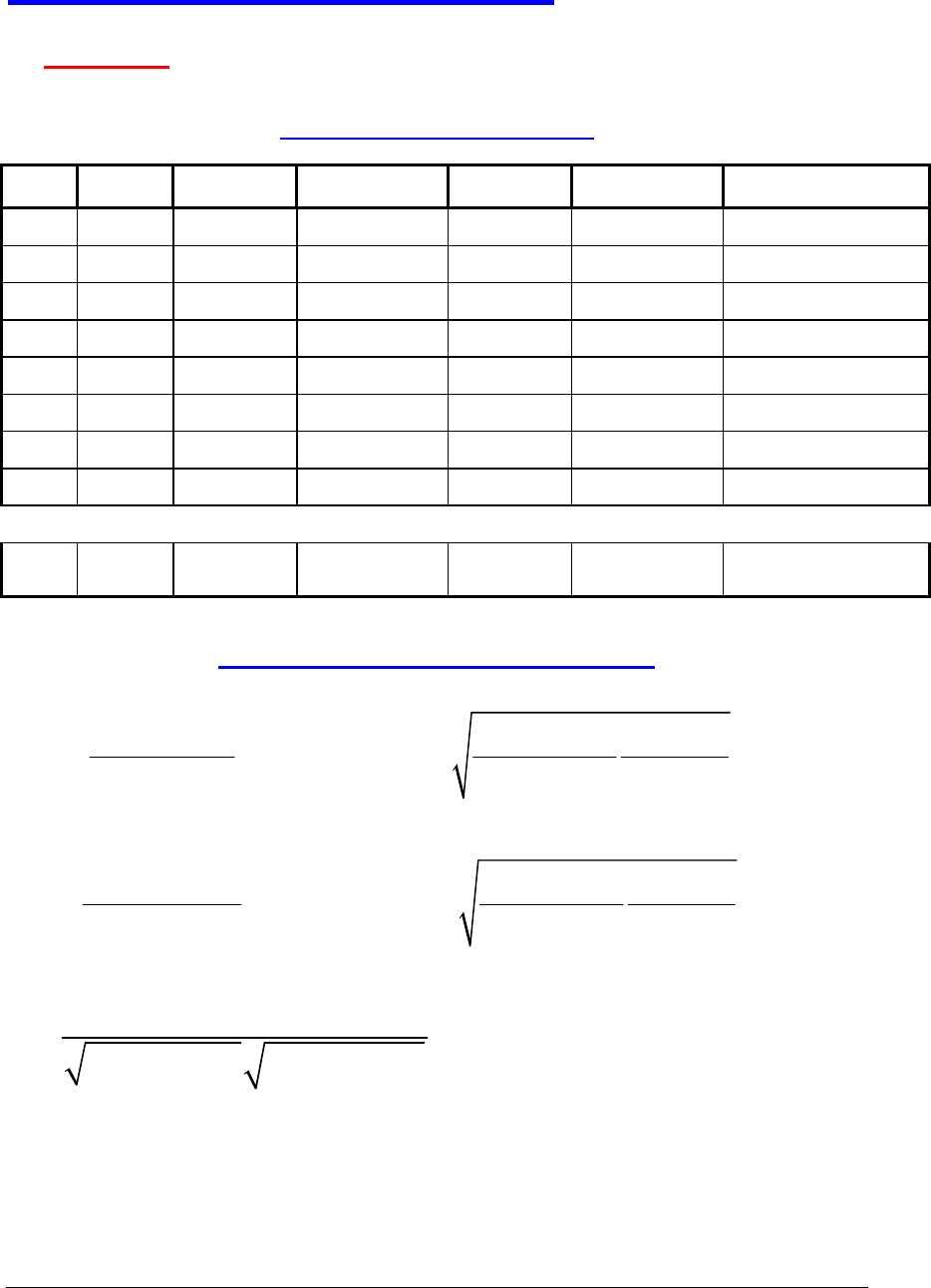
Presentación de los resultados
Ejemplo
Tabla de datos y cálculos
i x
i
y
i
x
i
y
i
x
i
2
y
i
2
(n+mx
i
-y
i
)
2
1 1 1.5 1.5 1.0 2.25 0.042
2 2 2.0 4.0 4.0 4.00 0.052
3 3 4.0 12.0 9.0 16.00 0.699
4 5 4.6 23.0 25.0 21.16 0.187
5 6 4.7 28.2 36.0 22.09 1.606
6 8 8.5 68.0 64.0 72.25 0.440
7 9 8.8 79.2 81.0 77.44 0.000
8 10 9.9 99.0 100.0 98.01 0.037
N=8 S
x
=44 S
y
=44 S
xy
=314.9 S
xx
=320 S
yy
=313.2
χ
2
=3.066
PARÁMETROS DEL AJUSTE :
2
2
(, )
= =
2
0.935 0.081
0.
(, )
3
2
60.512
xy x y
xx xx xx xx
xx y x xy
xx
xx xx xx xx
NS S S
Nnm
m(m)
NS SS NS SS N
SS SS
S
nm
n(n)=
NS SS NS SS N
χ
ε
χ
ε
−
==
−−−
−
== =
−−−
0.978
xy x y
xx x x yy y y
NS S S
r
NS S S NS S S
−
==
−−
Técnicas experimentales de Física General 7/7
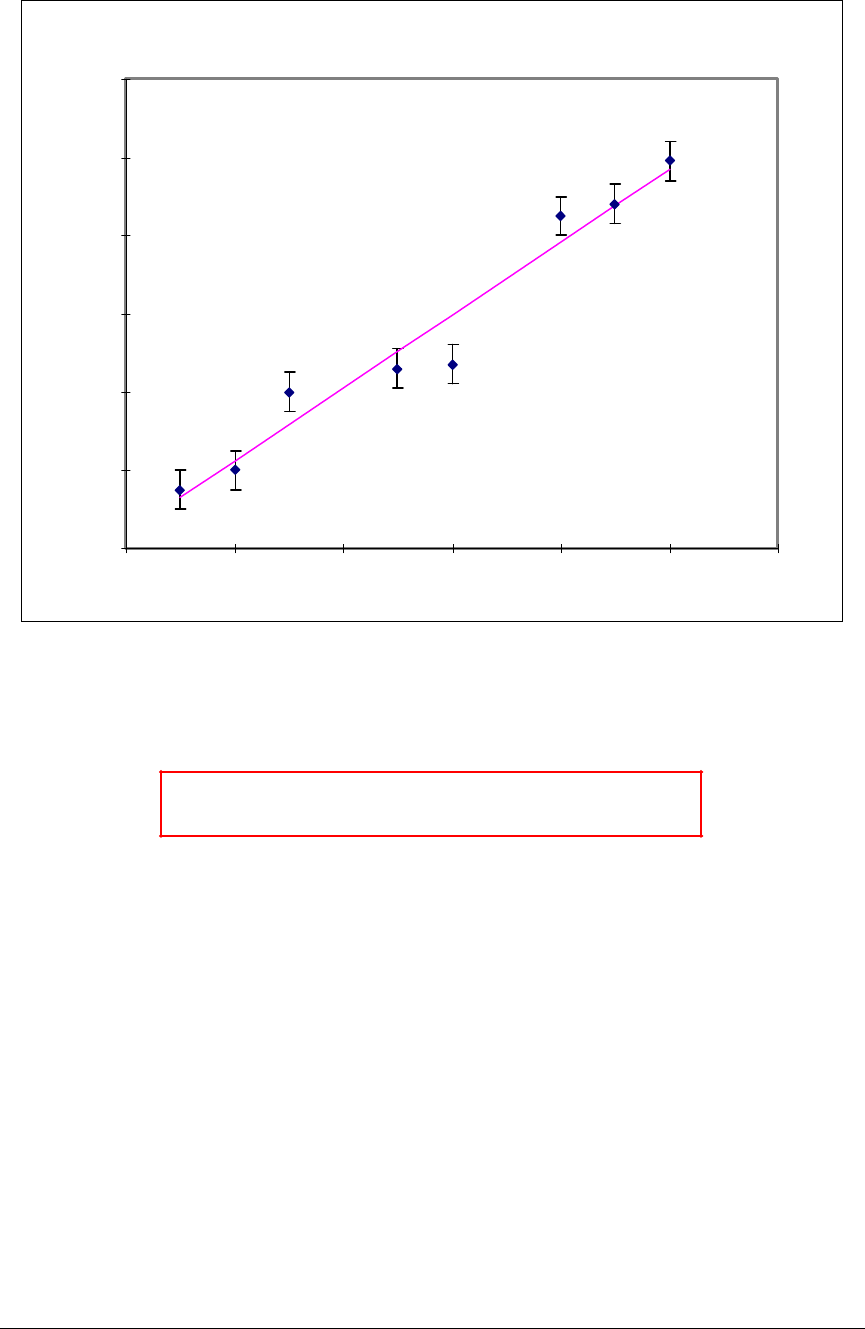
Ajuste de datos a una recta
0,0
2,0
4,0
6,0
8,0
10,0
12,0
0,0 2,0 4,0 6,0 8,0 10,0 12,0
x(unidades)
y(unidades)
()()
0.94 0.08 0.4 0.5yx±±=+
Ajuste de una recta por Mínimos Cuadrados.pdf
browser_emoji Estamos procesando este archivo...
browser_emoji Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
. . . . .