
ESTUDIO DEL COMPORTAMIENTO DINÁMICO
DEL SISTEMA CIRCULATORIO. INTERACCIÓN
SANGRE-VASOS SANGUÍNEOS
Mengarelli, G. Hernández, G.
Cátedra de Física Biológica. Facultad de Cs. Médicas. UNR.
CONTENIDOS
Introducción
Contenidos especícos
Ley general de Flujo
Pulsatilidad del ujo sanguíneo
Ley de continuidad – Relación entre área seccional y velocidad media en el sistema circulatorio
Resistencia hemodinámica
Unidades de resistencia hemodinámica
Ley de Poiseuille
Variación de la presión en el sistema circulatorio
Resistencias en serie
Resistencias en paralelo
Viscosidad de la sangre: otro determinante de la resistencia hemodinámica
Flujo laminar y turbulento - Número de Reynolds
Energética del ujo sanguíneo
Medición de la presión arterial
Efecto de la postura sobre la presión hidrostática
Propiedades de los vasos sanguíneos: distensibilidad
Ley de Hooke-comportamiento elástico de los vasos
Ley de Laplace
Tensión activa- presión crítica de cierre
INTRODUCCIÓN:
La evolución de las especies condujo a que los mamíferos superiores hayamos desarrollado importantes
capacidades y mecanismos para adaptarnos a las exigencias del entorno y así, sobrevivir; entre ellos podemos
destacar la existencia de un sistema cardiovascular exquisitamente especializado que otorga a los seres hu-
manos algunas ventajas por sobre otros animales de la Tierra.
Dicho sistema está integrado por: a) un órgano impar, muscular, hueco o cavitado: el corazón, comandado
por un mecanismo especializado de control propio, inuenciado por bras del sistema nervioso autónomo,
irrigado por una adecuada y característica geometría vascular, b) por un extenso, diverso y adaptable conjunto
de vasos sanguíneos, y c) por la sangre, uido que los recorre e interactúa con estos últimos, y que presenta
un comportamiento que podremos comprender mejor a partir del conocimiento de algunas leyes: análisis he-
modinámico.
379

Guía de Aprendizaje - Trabajo y Tiempo Libre
Si bien el análisis hemodinámico del corazón, genera gran interés y desafíos, no será abordado en esta
instancia de la currícula de grado. Por lo tanto, nos referiremos exclusivamente al sistema circulatorio, al que
dividiremos en dos grandes circuitos: el mayor o sistémico y el menor o pulmonar.
El ventrículo izquierdo da origen al circuito sistémico, a partir de la arteria aorta. Luego de aquí, iniciamos un
largo camino por otras arterias, de gran, mediano y pequeño calibre, para llegar a un sector no menos impor-
tante, el de las arteriolas. Éstas terminan en los capilares (hasta aquí, el lado arterial del circuito mayor), que
luego del sitio de intercambio dan origen a las vénulas. Así se da comienzo al lado venoso del circuito mayor,
que se continúa con las venas de pequeño, mediano y gran calibre, para desembocar en la aurícula derecha,
por medio de dos grandes venas: cava superior y cava inferior.
De manera complementaria, el ventrículo derecho da origen al circuito pulmonar a partir del nacimiento de la
arteria homónima. Desde aquí, en su camino a los pulmones surgirán las correspondientes bifurcaciones para
el ingreso a cada pulmón, replicando luego la división descripta anteriormente hasta el sector de capilares. Los
mismos dan origen al sistema venoso, con calibre progresivamente mayor hasta terminar en las cuatro venas
pulmonares, que desembocarán a nivel de la auricular izquierda.
La Física Biológica utiliza leyes y ecuaciones matemáticas, herramientas útiles que nos permiten comprender
los mecanismos que rigen nuestro funcionamiento, en este caso el sistema circulatorio.
Veremos ahora algunos conceptos especícos que usaremos frecuentemente y que nos permitirán entender
las leyes de la Hemodinamia.
Flujo: es el volumen de uído que circula por un tubo o vaso sanguíneo en la unidad de tiempo a través de un
área seccional perpendicular a la pared del mismo. Tiene como sinónimo caudal.
Desde la siología hablamos de gasto cardíaco o volumen minuto cardíaco (VMC) cuando nos referimos a
ujo; se lo expresa en litros/minuto, mililitros/segundo.
El volumen sistólico (VS) es una expresión particular para denir un ujo especíco (mililitros/latido), y junto
a la frecuencia cardíaca (FC) determinan el volumen minuto cardíaco, mediante una ecuación matemática que
los relaciona:
VMC= FC x VS
Volemia (o volumen sanguíneo total): es el volumen total de sangre de un individuo. Nos referimos a volemia
efectiva, cuando dicha sangre se encuentra en movimiento (circulante en los vasos sanguíneos), a diferencia
de aquella que, a modo de reserva, se mantiene en éxtasis en algunos órganos (hígado, bazo, circuito menor.
Surge de la suma del volumen globular total (VGT) y del volumen plasmático total (VPT). Aproximadamente es
el 6-7 % del peso corporal. Guarda relación directa con la masa magra corporal.
HOMBRE MUJER
Valor VST Normal 60 a 70 ml/kg 53 a 65 ml/kg
VGT 25 a 30 ml/kg 22 a 26 ml/kg
VPT 30 a 40 ml/kg 33 a 35 ml/kg
Frecuencia cardíaca: es el número de veces que se contrae el corazón por minuto. Sus valores de referencia
en el adulto normal son de 60 a 100 latidos/minuto. Es uno de los determinantes del volumen sistólico.
Área seccional transversal: para comprender este concepto tenderemos una línea imaginaria entre la luz y
la íntima del vaso rodeándolo en su totalidad, a modo de perímetro. La supercie limitada de esta manera es la
que denominamos área seccional transversal. A diferencia de éste último término, el área seccional transversal
total, es la suma de las áreas de cada uno de los vasos que se encuentran dispuestos en paralelo en un deter-
minado sector del circuito circulatorio,
Cuando se hace referencia al área seccional transversal total se está hablando de la suma de las áreas co-
rrespondientes a los vasos de un determinado sector del lecho circulatorio. Por ejemplo: la aorta ocupa un área
seccional transversal menor que las primeras ramicaciones arteriales.
380

A los nes prácticos se la calcula como el área de un círculo, y se la expresa en cm
2
, mm
2
.
Resistencia: es el conjunto de variables que se oponen al ujo. Está determinada tanto por factores de-
pendientes del sistema de tuberías (red vascular o bronquial) como por características del uido que circula
por ellas. El concepto de rozamiento del uido con las paredes del tubo que lo contiene, con la consecuente
pérdida de energía, también contribuye a modicar la resistencia. A los nes prácticos (clínicos) se la expresa
en mmHg x litros / minuto (UR: unidades de resistencia).
Viscosidad: es una propiedad que poseen los uidos, que se maniesta como una resistencia al ponerlos
en circulación o en movimiento. En función de las características de los uidos circulantes, esta resistencia
podrá ser expresada como la relación entre los esfuerzos tangenciales que tienden a deformarlos y el cambio
de velocidad entre dos capas concéntricas de uido separadas por una dada distancia. Este concepto será
ampliado más adelante. Depende de la temperatura y se expresa en Pascal/segundo o en centipoisse.
Presión hidrostática: es la fuerza por unidad de supercie que ejerce un uido (en reposo) contra las pare-
des del recipiente que lo contiene. Dicha fuerza está en relación al peso del uido que estemos considerando,
siendo el factor determinante del movimiento de la sangre. Es el valor que se registra con la toma habitual de
presión arterial y se la expresa en mmHg, Newton/m
2
, dinas/cm
2
.
Velocidad lineal media ó de ujo: es la distancia recorrida por una partícula del uído en la unidad de tiem-
po. A diferencia del caudal, con esta variable se describe cuan rápido es el ujo en determinados sectores de
la circulación. Se la expresa en mm/seg; cm/seg; m/seg.
Tensión: este concepto tiene diferentes acepciones: por ejemplo un músculo cuando es estirado está some-
tido a una tensión; cuando hablamos del estado anímico podemos decir “este trabajo me provoca mucha ten-
sión”, etc. De todos los signicados que podemos encontrar, según la bibliografía consultada, acordamos aquí
con la denición de tensión como: la fuerza por unidad de longitud aplicada tangencialmente a una supercie.
1- LEY GENERAL DE FLUJO
Esta ley nos dice que el ujo de sangre Q, a través de un lecho vascular dado depende de: 1) la fuerza impul-
sora ∆P, que es la diferencia de presión entre los extremos del sistema circulatorio (o de la parte del mismo en
estudio), y 2) la resistencia R, que dicho sistema ofrece al ujo de sangre:
Q (ujo)= ∆P (diferencia de presión)
R (resistencia)
La efectiva distribución del ujo a los distintos tejidos para satisfacer sus necesidades particulares de cada
momento, se logra controlando las dos variables que lo determinan: la diferencia de presión (∆P) y la resisten-
cia al ujo (R) de cada lecho vascular. Siendo esta última la principal variable determinante del mismo.
En cada territorio las arteriolas determinan la magnitud del ujo que atraviesa el lecho capilar gracias a que
su pared posee un importante componente muscular, modicando su calibre de acuerdo a la función (control
autonómico), a factores hormonales, humorales y a la actividad metabólica local.
El ujo en el circuito sistémico depende de la diferencia de presión entre el origen de la aorta (creada por el
ventrículo izquierdo) y la aurícula derecha, y de la resistencia periférica total, determinada principalmente por
las arteriolas. La circulación sistémica proporciona una fuente de sangre oxigenada de alta presión para irrigar
los órganos del cuerpo y drena la sangre venosa de retorno al corazón derecho. (g. 1)
Mientras que en el circuito pulmonar, el ujo sanguíneo depende de la diferencia de presión entre el origen
de la arteria pulmonar (presión creada por el ventrículo derecho) y la aurícula izquierda, y de la resistencia del
381

Guía de Aprendizaje - Trabajo y Tiempo Libre
lecho pulmonar debido principalmente a las arteriolas pulmonares. La circulación pulmonar tiene una presión
relativamente baja (alrededor de 1/5 de la que existe en las arterias sistémicas, con una presión media de 10
a 20 mmHg en la arteria pulmonar) y tiene la función especial de proporcionar una vía de baja resistencia para
que el ujo total de sangre que recorre el organismo atraviese los pulmones. Además del intercambio de gases
que aquí se produce, el circuito menor tiene una función secundaria como reservorio del volumen sanguíneo
para el corazón izquierdo (contiene cerca del 10% del volumen total) y dada la distensibilidad de sus paredes
(concepto que analizaremos más adelante) (10 veces mayor que aorta pero menor que las venas sistémicas,
estas últimas constituyen el único verdadero reservorio de sangre del organismo) le permite acomodar con
facilidad los grandes aumentos del ujo sanguíneo que pueden ocurrir (por ejemplo en un ejercicio físico) no
manifestando así un cambio sustancial de la presión. (g. 1)
Fig. 1 Sistema Circulatorio Sistémico y pulmonar (extraída de Rooke T.W., Sparks H.V. Cap.12
“Una revision de la circulación y la hemodinamia”, libro Fisiología Médica 2da. Ed.).
2- PULSATILIDAD DEL FLUJO SANGUÍNEO:
La principal característica que presenta el ujo sanguíneo en el sistema de las arterias (también denominado
de alta presión) es la de ser pulsátil. Aunque la salida de la sangre del corazón es intermitente, el ujo continuo
a los tejidos periféricos se consigue por la distensión (concepto que analizaremos más adelante) de la aorta y
de sus ramas durante la contracción ventricular (sístole) y por la retracción elástica de la pared de las grandes
arterias, con la consiguiente propulsión de la sangre hacia adelante durante la relajación ventricular (diástole).
En cada latido, el ventrículo izquierdo expulsa a la aorta un volumen de sangre de unos 90 ml en 0,3 a 0,4
seg. Esta eyección intermitente va acompañada de una dilatación de la aorta, lo que permite alojar el volumen
expulsado y de un aumento de la presión aórtica correspondiente a este cambio de volumen. Al nal de la eyec-
ción, la presión disminuye a medida que la sangre se desplaza hacia las arterias periféricas. Este incremento y
disminución alternativos de la presión constituye lo que se denomina onda de presión arterial (Fig 2)
382

Fig 2
Además, la eyección ventricular va acompañada de una brusca aceleración de la velocidad de la sangre en
la aorta, seguida de una desaceleración rápida y de un período de reposo, lo que corresponde a la onda de
velocidad.
Estas ondas (de presión y velocidad) se propagan desde el corazón hacia la periferia dada la elasticidad de
la pared de las arterias; es decir la fuerza motriz de la onda arterial proviene de la energía potencial elástica de
las arterias distendidas. Este fenómeno es análogo a la propagación de las olas del mar.
En la Fig 2 se puede observar que existe un valor máximo que alcanza la presión arterial denominada presión
sistólica (P
s
) y un valor mínimo, presión diastólica (P
d
) durante el ciclo cardíaco. Un valor medio de la presión
en el tiempo será más próximo a la Pd que a la Ps dado que, el tiempo que dura la diástole es el doble que
el de la sístole. Dicha presión arterial media (PAM) se determina aproximadamente mediante la siguiente
ecuación:
PAM = (P
s
+2 P
d
) /3
No se debe confundir PAM con presión del pulso (P
p
), está última es la diferencia entre la presión sistólica
y la diastólica:
P
p
= P
s
– P
d
La presión de pulso tiene valores distintos cuando se mide en diferentes sectores del lecho circulatorio: au-
menta hacia la periferia siendo uno de los factores que contribuyen a ello, la elasticidad no uniforme de la pared
vascular dada por la variabilidad en la composición y espesor de la pared.
3- LEY DE CONTINUIDAD
Esta ley establece que el ujo en un circuito cerrado, como podemos suponer al circulatorio, esto es sin
pérdidas ni ganancias de uido a lo largo del mismo, es el mismo en cada una de sus partes. Si el ujo no se
mantuviera constante debería haber ingreso de uido (si en alguna parte el caudal es mayor) o pérdida (si el
caudal es menor) y esto no es compatible con un circuito cerrado.
Recordemos que se dene ujo o caudal como el volumen de uido que atraviesa un área seccional, perpen-
dicular a su movimiento, en la unidad de tiempo, es decir:
F= V / t (1)
siendo F = ujo,
V = volumen y
383

Guía de Aprendizaje - Trabajo y Tiempo Libre
t = tiempo.
Si bien constituye una estimación de la velocidad con que se desplaza el uido, es diferente de la velocidad
lineal media (v) que es la velocidad con que se mueve cada partícula del líquido:
v =x / t
siendo x = longitud y
t = tiempo
El volumen de uido que atraviesa el área seccional (S) a lo largo de una distancia (x) es:
V = S. x
Es decir expresado mediante una ecuación matemática la ley de continuidad es:
F = S. v = constante
Siendo F= ujo
S= área seccional
v= velocidad lineal media
Esta ley explica que un río es más caudaloso que otro si por una sección del mismo pasa un volumen mayor
por unidad de tiempo. Para ello debe tener un lecho más amplio o bien un lecho igual por el que circula el agua
a mayor velocidad.
En condiciones siológicas, el ujo es el mismo a lo largo del circuito (como lo implica la ley) pero no es
constante en el tiempo. Por ejemplo una persona durmiendo (situación basal) tiene un ujo sanguíneo infe-
rior al normal (3 lt / min), y cuando se levanta alcanza el valor “normal” de 5 lt / min, pero si comienza a hacer
actividad física volverá a modicarlo según la intensidad del ejercicio y el grado de entrenamiento (por ejemplo
puede llegar a 15 lt / min) y al nalizar la actividad su ujo sanguíneo volverá a disminuir al valor de 5 lt/min (es
decir, que retoma el valor que tenía dicha persona en condiciones “normales”).
Como enunciamos anteriormente, a cada instante, el ujo sanguíneo toma el valor adecuado a la actividad del
momento. Sin embargo la ley de continuidad se cumple siempre, porque en cada instante el ujo que el corazón
impulsa dentro de la aorta es igual al que uye en las arterias repartido entre las ramas paralelas correspon-
dientes, y al que atraviesa los lechos capilares, y también al que regresa al corazón por las venas cavas. De
la misma manera, el ujo de sangre que impulsa el ventrículo derecho a la arteria pulmonar debe ser igual al
que atraviesa el circuito sistémico y debe tener el mismo valor en los distintos sectores (arterias, arteriolas,
capilares, vénulas, venas) del sistema circulatorio pulmonar.
El área seccional dene la velocidad lineal de las partículas: si el mismo volumen líquido debe atravesar un
angostamiento, es necesario que cada partícula se mueva a mayor velocidad en dicha zona.
La arquitectura del lecho vascular hace que la suma de las áreas seccionales de los vasos hijos supere al área
seccional del vaso madre (Fig. 3).
A1 < A2 + A3 + A4
Fig 3 -Esquema del área seccional de un vaso madre
y de los vasos hijos
384

Así, si bien los vasos se van haciendo cada vez más pequeños desde aorta a capilares, el número de rami-
caciones compensa y supera la disminución de sección de los vasos de modo que la sección conjunta de todos
los vasos paralelos va en aumento (como se muestra en la tabla 1); y por ende la velocidad con que circulan
la sangre decrece.
Tabla 1: Geometría del lecho vascular del perro
TIPO DE VASO DIAMETRO (mm) Número de vasos Area total (cm2)
aorta 10 1 0.78
grandes arterias 3 40 3
ramas principales 1 600 5
ramas terminales 0,6 1.800 5
arteriolas 0,02 40.000.000 12,5
capilares 0,008 1.200.000.000 600
vénulas 0,03 80.000.000 570
venas terminales 1.5 1.800 30
venas principales 2,4 600 27
grandes venas 6,0 40 11
vena cava 12,5 1 1,3
Si se reemplazara el conjunto de vasos paralelos de un nivel del circuito por un único vaso equivalente,
encontraríamos que de aorta en adelante se iría ensanchando hasta 150 veces a nivel de las arteriolas y 800
veces a nivel capilar. A la inversa en territorio venoso, la sección del vaso equivalente a la suma de los vasos
en paralelo iría disminuyendo a medida que las venas convergen en otras mayores hasta las venas cavas cuya
área seccional es sólo 1,5 veces mayor que la de aorta. El gran incremento de área a nivel capilar se debe a
que, si bien cada uno de ellos es muy pequeño, hay un gran número de capilares en paralelo.
3-1 Relación entre área seccional y velocidad media en el sistema circulatorio
La velocidad lineal media de la sangre a través de los diversos segmentos puede calcularse a partir de cono-
cer la geometría de la circulación sistémica, dado que en cualquier punto la velocidad lineal media es igual al
ujo total dividido por el área transversal del lecho vascular.
La aorta humana tiene un diámetro similar a un dedo pulgar, digamos dos centímetros, por lo tanto el área
seccional (supercie del círculo) es: π .r
2
= 3,14 (1cm)
2
= 3,14 cm
2
. Dado que en condiciones de reposo, salen
del corazón 5 lt / min, la velocidad media en la aorta será de 28 cm / seg, es decir que cada glóbulo rojo avanza,
en promedio, a 28 cm / seg.
A medida que la aorta se divide el área seccional total aumenta y la velocidad lineal media disminuye (Fig. 4).
Cada capilar es extraordinariamente angosto (diámetro menor al de un glóbulo rojo), pero dado que el lecho
capilar total contiene muchos miles de millones de capilares en paralelo, el área seccional total es 800 veces
mayor que la de aorta y como el ujo que los atraviesa debe ser el mismo (5 lt / min), la velocidad lineal media
deberá ser 800 veces menor a la de la aorta, es decir 0,035 cm / seg.
Este enlentecimiento de la sangre en los capilares proporciona un contexto altamente favorable para el in-
tercambio de gases y metabolitos a lo largo de su pequeña longitud. Se pueden considerar que miden 1 mm
en promedio, por tanto un glóbulo rojo (como cualquier otra partícula de la sangre) tarda aproximadamente
3 segundos en atravesar el lecho capilar. Por otro lado si los 5 lt / min debieran pasar por un solo capilar, se
necesitarían 5. 10
7
seg = 1 año y 8 meses.
El área seccional de las venas cavas es aproximadamente el doble que la de la aorta, por lo tanto la velocidad
media es cercana a la mitad de la que posee la aorta descendente.
385

Guía de Aprendizaje - Trabajo y Tiempo Libre
En la circulación pulmonar, que parece ser simplemente una versión en pequeño de la circulación sistémica
(de hecho se la denomina circulación menor) necesariamente existe la misma relación entre la velocidad media
y el área seccional. El área de la arteria pulmonar principal es similar al de la aorta, por lo tanto las velocidades
medias son similares. La arteria pulmonar se ramica en forma sucesiva como el sistema de vías aéreas al
cual irriga, luego dan lugar al lecho capilar, la unión de los capilares origina las pequeñas venas pulmonares
que se reúnen en las cuatro venas que drenan en la aurícula izquierda. Como el área total de las cuatro venas
pulmonares es mayor que el de la arteria pulmonar principal la velocidad media en ella es menor.
Fig 4 -Área seccional y velocidad en los
distintos sectores del sistema circulatorio
sistémico.
4- RESISTENCIA HEMODINÁMICA
Tal como se puede intuir, la resistencia hemodinámica es la medida cuantitativa de la dicultad que debe
vencer la sangre para uir a través de una dada sección del lecho vascular. Como se enunció anteriormente, es
la relación entre la fuerza conductora, es decir la caída de presión entre los extremos de esa sección y el ujo:
R = ∆P/ F donde ∆P = P
en el extremo anterior
– P
en el extremo posteior
4-1 Unidades de resistencia hemodinámica
En Medicina, la presión sanguínea se expresa en mmHg (por lo tanto ∆P tiene estas unidades) y el ujo en
litros / minuto, por lo tanto, las unidades de resistencia son: mmHg / litro / minuto, o como se denomina co-
múnmente: U.R. También puede expresarse en el sistema c.g.s, en cuyo caso ∆P se expresa en dinas / cm
2
y
el ujo en cm
3
/ seg de lo que resulta la unidad de resistencia en el sistema c.g.s.: dinas x seg / cm
5
.
5- LEY DE POISEUILLE
La ley de Poiseuille se vincula con el caudal de uido que circula por un conducto. En un tramo de tubo la
presión tiene un valor P
1
en el extremo izquierdo y en el extremo derecho la presión es P
2
. Esta diferencia de
presiones es la que hace moverse al uido a lo largo del tubo. El caudal (volumen por unidad de tiempo) depen-
de de la diferencia de presiones (P
1
- P
2
), de las dimensiones del tubo y de la viscosidad del uido. La relación
entre estas magnitudes fue determinada por el francés J. L. Poiseuille y a esta relación se le conoce como Ley
de Poiseuille.
386
Siendo, Caudal = ujo
P
1
- P
2
= ∆P (diferencia de presión entre los extremos del circuito) *
R = radio del tubo,
η = viscosidad del líquido y
L = longitud del tubo.
Esta ecuación contiene una constante que es π/8.
Poiseuille estudió los factores determinantes de la resistencia al ujo de un líquido en:
1) tubos rígidos, de calibre uniforme y de longitud mucho mayor que el radio de los vasos,
2) líquidos newtonianos,
3) ujo estable y laminar.
La ecuación de Poiseuille ilustra la importante relación entre la resistencia vascular y los factores que la de-
terminan: 1) el radio del vaso, 2) la longitud del vaso y 3) la viscosidad de la sangre:
R = 8 l η / π r
4
como mencionamos anteriormente 8/π es una constante.
De ella se deduce que si cualquiera de los dos factores últimos se duplica, el ujo caerá a la mitad (o bien,
para que el ujo permanezca constante, el gradiente de presión debe duplicarse). La ecuación también enfatiza
la enorme inuencia del radio del vaso; si el radio se duplica, el ujo aumenta 16 veces.
El control de la distribución del ujo de sangre puede ser logrado por dos caminos: a) modicando la presión
conductora ∆P (que modica el ujo total) y b) controlando la resistencia R en cada lecho particular. La gran
importancia de la resistencia reside en que su control es el mecanismo que permite adaptar el ujo a los dife-
rentes órganos y tejidos conforme a sus necesidades especícas.
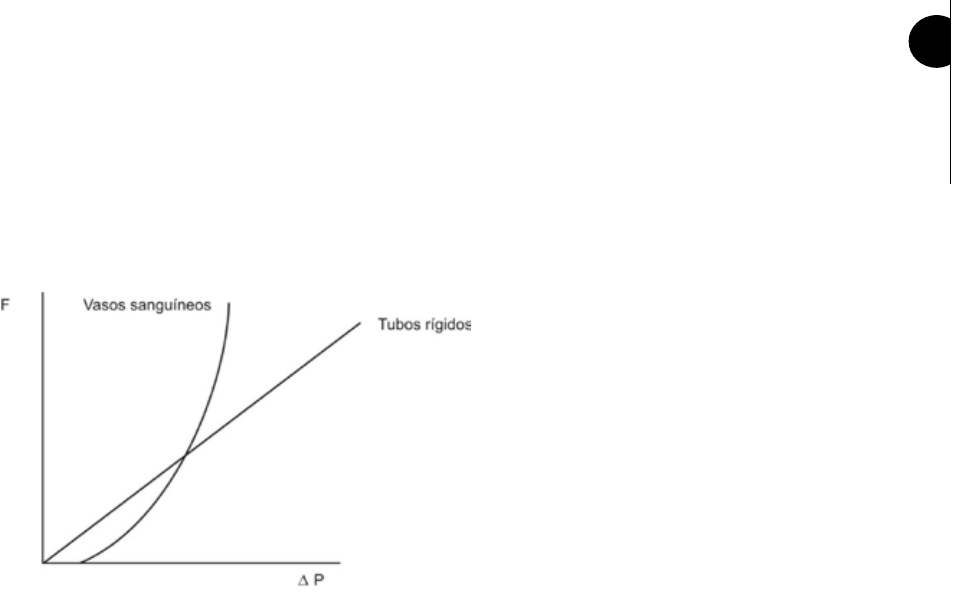
Fig. 5 Relación ujo-diferencia de presión para
un sistema de tubos rígidos y para los vasos san-
guíneos.
Del análisis de la Fig. 5 surge que en un sistema hidráulico la resistencia es independiente de la diferencia
de presión que hace circular el uido. Pero los experimentos realizados en los vasos de la oreja de conejo
demostraron que no ocurre lo mismo en el sistema circulatorio, es decir la representación gráca no es una
recta. En él la resistencia varía cuando varía la diferencia de presión que mueve la sangre y esto se debe a
que los vasos sanguíneos no son vasos rígidos y su radio se modica cuando cambia la presión en su interior.
A pesar de ello la ley de Poiseuille es una buena aproximación que nos permite explicar las modicaciones de
ujo que suceden en el organismo.
Las condiciones anteriormente enunciadas no se dan en el sistema circulatorio debido a que:
1. los vasos sanguíneos son distensibles y presentan ramicaciones y modicaciones de su radio.
387

Guía de Aprendizaje - Trabajo y Tiempo Libre
2. la sangre es un líquido no newtoniano, su viscosidad varía con la velocidad de de deslizamiento o de
corte.
3. el ujo es pulsátil (recordemos que el ujo de sangre además es contínuo, concepto que debemos diferen-
ciar de pulsatilidad) en el territorio arterial y la sangre uye a veces de modo turbulento.
* Es importante remarcar que P
1
en el circuito pulmonar es el valor correspondiente a la presión arterial media
pulmonar, y en el circuito sistémico, a la presión arterial media sistémica (PAM); y P
2
representa la presión
venosa pulmonar ó sistémica (PVC) respectivamente.
5-1 Variación de la presión en el sistema circulatorio
Los sectores del sistema circulatorio (arterias, arteriolas, capilares, vénulas, venas) se encuentran conecta-
dos en serie. Por lo tanto el ujo es el mismo en todos esos sectores, pero la diferencia de presión entre los
extremos de cada sector es distinta. Como se puede deducir de la Fig. 6: el ∆P es distinto para cada sector.
En la tabla 2 se muestran las resistencias relativas de los distintos sectores del lecho vascular lo cual permite
comprender mejor dicha gráca.
Fig. 6. Caída de la presión a lo largo del circuito sistémico y pulmonar
Tabla 2 Resistencias relativas de los sectores del lecho vascular
AORTA 4 %
ARTERIAS GRANDES 5 %
ARTERIAS MEDIANAS 10 %
ARTERIAS TERMINALES 6 %
ARTERIOLAS 41 %
CAPILARES 27 %
VENULAS 4 %
VENAS TERMINALES 0.3 %
VENAS MEDIANAS 0,7 %
VENAS GRANDES 0,5 %
VENA CAVA 1,5 %
388

La tabla 2 muestra que el sector de mayor resistencia son las arteriolas (41%) y por lo tanto en este sector del
sistema circulatorio se produce la mayor caída de presión (Fig 6). Esto se debe a la relación entre resistencia y
el radio del vaso sanguíneo (ley de Poiseuille, que se encuentra elevado a la cuarta potencia), es decir a pesar
de que el número de arteriolas es mayor al número de arterias que le dan origen es mayor la diferencia en el
radio de las arteriolas respecto del radio de las arterias.
Como se dijo anteriormente los distintos tipos de vasos que constituyen el sistema circulatorio se hallan
conectados en serie y los distintos órganos se conectan al corazón en forma “directa” o en paralelo (Fig 1).
Entonces podemos analizar como es la resistencia que se ofrece al ujo sanguíneo en su recorrido:
1) RESISTENCIAS EN SERIE
En este caso el ujo que atraviesa cada resistencia es el mismo, lo que varia es el ∆P entre los extremos de
cada resistencia (Fig 7). El ∆P entre el inicio y el nal va a ser la suma de los ∆P parciales.
Fig. 7. Resistencias en serie
Recordemos que R = ∆P / F, por lo tanto la resistencia total y la ∆P total tienen la siguiente relación es Rt =
∆Pt / F y reemplazando ∆Pt por la suma de los ∆P parciales queda:
Rt = (∆P
1
+ ∆P
2
+ ... + ∆P
i
) / F = ∆P
1
/ F + ∆P
2
/ F+ ... + ∆P
i
/ F = R
1
+ R
2
+ ...+ R
i
es decir que: Rt = R
1
+ R
2
+... + R
i
EJEMPLOS DE RESISTENCIA EN SERIE
En la circulación periférica existen dos ejemplos de lechos capilares en serie (Fig 8): 1) la circulación portal y
la esplénica, y 2) la circulación de los glomérulos y los túbulos renales.
Fig. 8 Ejemplos de resistencias en serie
2) RESISTENCIAS EN PARALELO
En este otro caso el ∆P a través de cada resistencia es el mismo, y el ujo que atraviesa cada resistencia será
inversamente proporcional al valor de ésta, siendo el ujo total la suma de los ujos parciales.
389

Guía de Aprendizaje - Trabajo y Tiempo Libre
Fig. 9 Resistencia en paralelo
Rt = ∆P / Ft = ∆P / (F
1
+F
2
+ ..+ F
i
)
Reordenando la ecuación queda :
1 / Rt = F
1
/∆P + F
2
/∆P + ... + Fi / ∆P
y en consecuencia: 1 / Rt = 1 /R
1
+ 1/ R
2
+.... + 1/ R
i
De lo que resulta que la resistencia total es menor que cualquiera de las resistencias componentes y que el
agregado de una nueva resistencia disminuirá la resistencia total.
EJEMPLO DE RESISTENCIA EN PARALELO
En la circulación periférica casi todos los órganos están dispuestos en paralelo (Fig 1), por lo tanto, aumentos
o disminuciones moderados de la resistencia en un órgano dado pueden no tener un impacto importante sobre
la presión sanguínea. Sin embargo existen diferencias enormes en el ujo a través de los diversos órganos en
reposo (y por lo tanto hay grandes diferencias en las resistencias regionales ya que la presión de perfusión
es la misma). Podemos observar las diferencias de dichos valores para los distintos órganos en los siguientes
ejemplos:
Resistencia hepática: 127 U.R.
Resistencia renal: 76 U.R.
Resistencia del cerebro: 127 U.R.
Resistencia de la piel: 190 U.R.
Resistencia total: 19 U.R.
6- VISCOSIDAD DE LA SANGRE. OTRO DETERMINANTE DE LA RESISTENCIA HE-
MODINÁMICA
En gran parte de la circulación, el ujo sanguíneo es laminar, excepto en las válvulas y ciertas áreas -como
ocurre en regiones patológicamente estrechas producidas por aterosclerosis- donde pueden observarse uc-
tuaciones aleatorias de la presión y la velocidad (ujo turbulento).
Si el ujo es laminar, la sangre uye a través de los vasos en una forma “ordenada”, con una velocidad de ujo
nula en la pared vascular que aumenta en forma progresiva hacia el centro del vaso (Fig 10). Si se consideran
las capas de líquido circulando con diferente velocidad, entre ellas habrá una fricción que ofrece resistencia al
deslizamiento. El grado de fricción y el valor de la resistencia que ofrece están determinados por la viscosidad
del líquido.
390
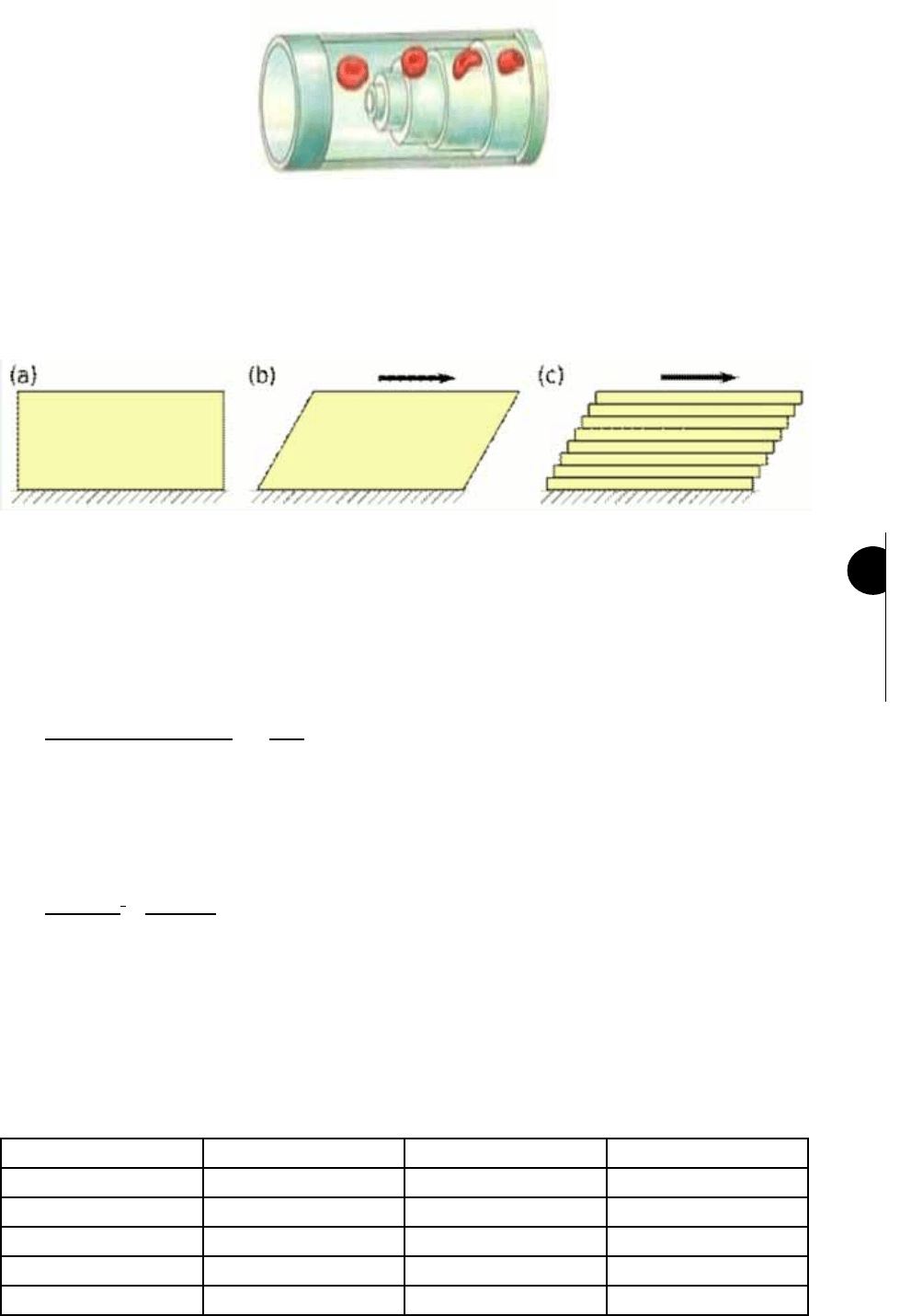
Fig. 10 Velocidad de ujo de las capas líquidas en forma telescópica.
Consideremos un líquido constituido por n capas líquidas colocado entre dos láminas de vidrio distantes una
longitud d y de supercie S. Si la lámina inferior está ja, al aplicar una fuerza (F) tangencial sobre la lámina
superior provocará un deslizamiento de las capas de líquido (Fig. 11).
Fig 11
La relación entre tensión de deslizamiento (F/S) y el índice de deslizamiento (∆v/∆x) (denida como el cam-
bio de velocidad entre dos capas de líquido vecinas dividida por la distancia que las separa ∆x) se denomina
viscosidad (η), es decir:
η = tensión de deslizamiento = F/ S
índice de deslizamiento ∆v/∆x
Analizando la ecuación anterior se pueden obtener las unidades en que se expresa la η:
[η] = dinas/ cm
2
= dinas.seg = poisse
1 / seg cm
2
Equivalencia de las unidades de η:
1 centipoisse = 0,01 poisse = 1 mili Pascal. seg ( mPa. seg)
Tabla 3 - Viscosidad de diversos líquidos a 20 ºC (expresada en centipoisse ó mPa.s)
éter etílico 0,233 mercurio 1,554
cloroformo 0,58 nitrobenceno 2,03
benceno 0,652 glicol 19,9
agua 1,005 aceite de oliva 84
alcohol etílico 1,200 aceite de castor 986
glicerol 1,49
391

Guía de Aprendizaje - Trabajo y Tiempo Libre
Tabla 4- Viscosidad de líquidos biológicos ((expresada en centipoisse ó mPa.s)
líquido cefalorraquídeo 1,024
orina 1,00-1,14
sangre entera ( a alta velocidad de deformación) 4,5
plasma 1,6
suero 1,4
El plasma se comporta como líquido newtoniano (viscosidad constante a diferentes velocidades de desliza-
miento de las capas líquidas), pero a causa de los eritrocitos suspendidos, los cambios de la viscosidad de la
sangre entera son pronunciadamente no lineales con las variaciones de velocidad de deslizamiento.
7- FLUJO LAMINAR Y TURBULENTO - NÚMERO DE REYNOLDS
El ujo laminar de un uido consiste en el desplazamiento del mismo en innitas capas que se deslizan una
sobre otras con velocidades que van creciendo desde las paredes hacia el centro de la corriente, en forma de
tubo telescópico (Fig 9). En ciertas condiciones el ujo de la sangre deja de ser laminar y pasa a ser turbulento,
es decir un ujo desordenado con formación de remolinos. (Fig.12)
La consideración del ujo turbulento es muy importante porque la existencia del mismo supone un aumento del
rozamiento de la sangre al uir, que en algunos sectores tiene sentido inverso. Ello tiene como consecuencia
una caída mayor de la presión y por lo tanto un mayor consumo de energía por parte del corazón para crear un
∆P mayor y efectivo para garantizar la circulación. Como se observa en la Fig. 12: ujo en función de ∆P para
un tubo rígido y sin ramicaciones, a medida que crece el ∆P el ujo también se modica en el mismo sentido
pero el aumento del ∆P es mayor para un mismo incremento de ujo cuando el ujo se hace turbulento.
Fig.12 Relación ujo- ∆P en ujo laminar y turbulento
Cuando el ujo es turbulento, el rozamiento de la sangre origina ruidos que pueden ser percibidos con el
estetoscopio (auscultados) o menos frecuentemente, directamente con el oído si la intensidad de aquellos es
suciente. En algunos casos el fenómeno también puede ser palpable. Los soplos que se auscultan en deter-
minadas condiciones (estrechez de una válvula cardiaca o de un vaso sanguíneo) son por la existencia de ujo
turbulento.
Se puede estimar la probabilidad de ujo turbulento a través del cálculo del denominado Número de Rey-
nolds ó bien de la velocidad crítica. Primero veremos cómo calcular el Número de Reynolds. Este depende
de la geometría del vaso (radio) y de características de la sangre (viscosidad, densidad y velocidad lineal media
de las partículas que la componen), que se puede resumir en la siguiente ecuación:
Nr = v .δ. r / η
392

siendo v: velocidad lineal media r : radio del vaso
η : viscosidad de la sangre
δ : densidad de la sangre
El valor del Nro. de Reynolds a partir del cual se considera la probabilidad de que ocurra ujo turbulento
depende de ciertas características del vaso sanguíneo, pero en general se estima que un valor mayor a 1000
corresponde a un ujo turbulento.
La otra manera de averiguar la probabilidad de que el ujo sanguíneo sea turbulento se deriva de la anterior.
Esto es, despejar de la ecuación anterior la velocidad para un Nro. de Reynolds igual a 1000 (es decir un nro.
de Reynolds a partir del cuál el ujo es probablemente turbulento), esa velocidad es denominada velocidad
crítica. Esta velocidad crítica es la velocidad lineal media máxima que puede tener la sangre para que el ujo
sea laminar. Si la velocidad con que circula es mayor a este valor es probable que el ujo sea turbulento.
Vc = Nr η / δ . r
Consideremos un ejemplo: si un líquido cuya viscosidad es 0,028 poise y su densidad de 1,024gr/ cm3 circula
por un tubo de 1 cm de radio, la velocidad crítica estará dada por:
Vc = 1000 x 0,028 poise / 1,024 gr/cm
3
x 1 cm = 27 cm / seg
Esto signica que si la velocidad de circulación es superior a 27 cm/ seg el régimen probablemente será tur-
bulento y por debajo de esa velocidad será laminar.
El ujo sanguíneo puede hacerse turbulento cuando:
1. la velocidad de ujo sanguíneo aumenta (ejercicio)
2. la viscosidad de la sangre disminuye (anemia, ebre)
3. se modica el radio del vaso. Si el radio del vaso sanguíneo aumenta (vasodilatación), la ecuación pre-
vé que aumenta la probabilidad de turbulencia. Por el contrario, si el radio del vaso disminuye, implica
un aumento de la velocidad lineal media para mantener el ujo constante (ley de continuidad) y este
aumento de velocidad estima también una mayor probabilidad de turbulencia. Por consiguiente hay que
considerar ambas variables (radio del vaso y velocidad lineal) en conjunto. La dilatación de un sector
en un vaso (aneurisma) producirá una variación brusca de la velocidad tanto en la entrada de sangre al
ensanchamiento, como en su salida a un sector más angosto; ésto aumenta fuertemente la probabilidad
de turbulencia.
8- ENERGÉTICA DEL FLUJO SANGUÍNEO
El teorema de Bernoulli es una aplicación del concepto de que el gradiente de presión no es la única fuerza
impulsora del ujo, otras fuerzas -la gravedad y la inercia- pueden mover el ujo incluso en contra de un gra-
diente de presión.
El teorema de Bernoulli, que es una consecuencia del primer principio de la termodinámica, establece que la
energía total es constante en todos los puntos de un circuito simple formado por tubos rígidos por los que cir-
cula un líquido ideal (sin viscosidad, es decir, sin rozamiento). Su uso en el estudio de la circulación sanguínea
puede dar lugar a interpretaciones equivocadas y a contradicciones aparentes, por lo cual veremos primero en
detalle las transformaciones energéticas que ocurren en un líquido ideal que circula por un sistema más simple
que el circulatorio.
La energía total (Et), que posee un uido moviéndose por un conducto cerrado permanece constante a lo
largo de todo el circuito y corresponde a la suma de tres formas de energía:
393
Este documento contiene más páginas...
Descargar Completo
52 - El problema del tiempo - Colovini.pdf
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.