
Modalidad virtual
Matemática
UBA XXI – MÁTEMATICA - Ecuaciones e Inecuaciones
1
ECUACIONES E INECUACIONES CON UNA INCOGNITA
Ecuaciones
no lineales
Hasta ahora resolvieron ecuaciones de primer grado con una sola incógnita de la forma
ax + b = 0 (ó que se reducen a ella). Vamos ahora a resolver otro tipo de ecuaciones,
que no pueden reducirse a ecuaciones de este tipo.
Ecuaciones
1
de segundo
grado
Se conoce como ecuación cuadrática o ecuación de segundo grado con una
incógnita a toda ecuación de la forma ax
2
+ bx + c = 0 (a0, y a, b y c números
reales).
Los números a, b y c son los coeficientes de la ecuación.
Por ejemplo, es una ecuación de segundo grado:
3x
2
+ 2x –5 = 0, donde a = 3; b = 2 y c = -5.
Aunque expresadas de otra manera, son también ecuaciones de segundo grado:
8x
2
= 32
-x
2
+ x = 0
4x
2
- 16 = 0
(8x – 2) ( 2x + 3) = 0
(2x – 3)
2
= 16
En algunos casos es relativamente fácil resolver una
ecuación de segundo grado.
Revisaremos, mediante ejemplos, cómo hacerlo.
Resolver una ecuación
es encontrar los
valores de la incógnita
que hacen verdadera
la igualdad.
Ejemplo 1. Resolver (x – 2) ( x + 3) = 0
Solución
Podemos observar que la expresión en el primer miembro es un producto entre números
reales.
Para que este producto sea igual a cero es suficiente que lo sea uno de factores.
Las soluciones de una
ecuación de segundo
grado se llaman raíces de
la ecuación cuadrática
En este caso x – 2 = 0 ó x + 3 = 0.
Luego, las soluciones son
x = 2 ó x = -3
ya que cualquiera de estos números anula a uno de los
paréntesis.
Así es S = {2; -3} el conjunto solución de la ecuación.
1
Elizondo, Giuggiolini, Módulo 2, Articulación Media Universidad; UBA XXI, 2007

UBA XXI Modalidad virtual
Matemática
UBA XXI – MÁTEMATICA - Ecuaciones e Inecuaciones 2
Ejemplo 2. -x
2
+ x = 0
Solución
Sacando factor común “x” se tiene: -x
2
+ x = x ( -x + 1) = 0
Con lo que la ecuación se puede resolver en forma similar a la anterior.
Por lo tanto, las soluciones son: x = 0 ó x = 1.
Y S = {0; 1}
Ejemplo 3. 4x
2
- 16 = 0
Solución.
La expresión en el primer miembro es una diferencia de cuadrados. Podemos
escribir:
4x
2
- 16 = (2x + 4) (2x – 4) = 0
Y nuevamente las raíces se encuentran al tener en cuenta que para que
un producto entre dos factores sea cero es suficiente que lo sea uno de
ellos. Así las soluciones son:
x = - 2 ó x = 2
• También se puede resolver esta ecuación de la siguiente manera:
4x
2
- 16 = 0
Dividiendo por 4 ambos miembros: x
2
– 4 = 0
Sumando miembro a miembro 4, es: x
2
= 4
De donde : 4x
2
Por lo que |x| = 2
y esto es cierto si x = 2 ó x = - 2.
¡Cuidado!
2
Si a es un número real
cualquiera |a|a
2
Con lo que se llega a la misma solución.
Luego es S = { -2; 2}
Ejemplo 4: x
2
+ 4 = 0
Solución
Si se escribe la expresión anterior en la forma x
2
= - 4
se puede afirmar que esta ecuación no tiene soluciones reales pues no existe ningún
número real que elevado al cuadrado sea negativo.
Ejemplo 5. (2x – 3)
2
= 16
Solución
Tomando raíz cuadrada en ambos miembros de la igualdad es:
16)3x2(
2
Esto es posible hacerlo ya que estamos seguros que (2x – 3)
2
0.
La igualdad anterior puede escribirse como
|2x –3| = 4
ya que aa
2
.
2
Ver anexo Valor Absoluto
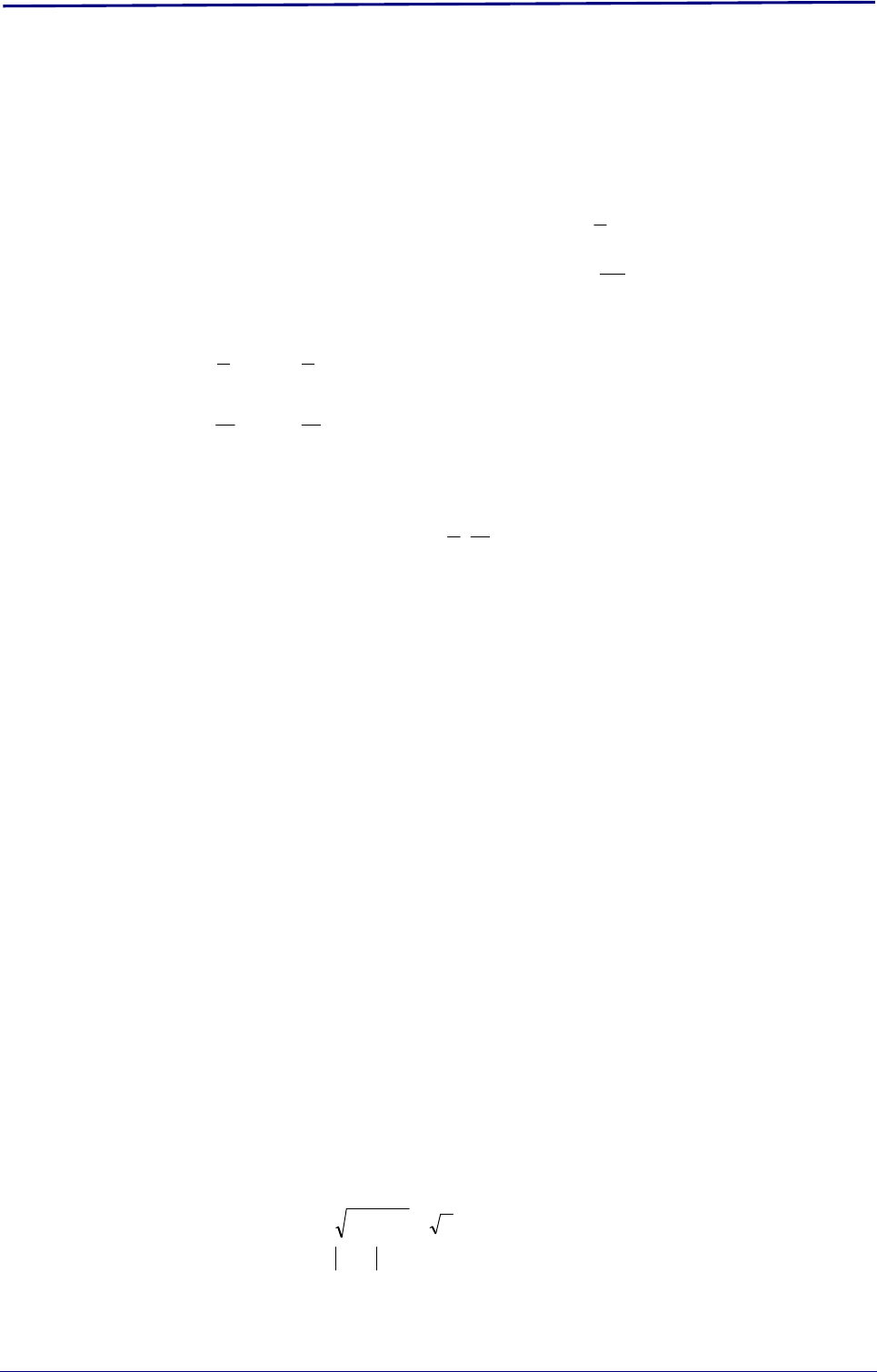
UBA XXI Modalidad virtual
Matemática
UBA XXI – MÁTEMATICA - Ecuaciones e Inecuaciones 3
Luego es:
2x – 3 = 4 ó 2x - 3 = - 4
ya que si |a| = 4 a puede ser 4 ó a puede ser –4.
Entonces si
2
1
xes43x2
2
7
xes43x2
Vemos si son soluciones de la ecuación dada (2x-3)
2
= 16
16(-4)3)-(-13
2
1-
2.;
2
1-
xSi
1643)-(73
2
7
.2;
2
7
xSi
22
2
22
2
Como verifican la ecuación dada, el conjunto solución de la ecuación es
2
1-
;
2
7
S
En los ejemplos anteriores fue posible hallar las soluciones de las ecuaciones planteadas
recurriendo a propiedades conocidas de la igualdad y de los números reales.
Otros casos pueden ser más difíciles de resolver ya que no aparece claro cómo despejar
la incógnita pues ésta aparece con distinto grado en los términos de la ecuación.
Por ejemplo en:
x
2
+ 6x + 9 = 4
Ejemplo 6. x
2
+ 6x + 9 = 4
Solución
¿Es posible escribir la expresión en alguna de las formas anteriores?
En realidad sí ya que el primer término de la igualdad es el desarrollo de (x + 3)
2
Veamos:
(x + 3)
2
= (x + 3) .(x + 3) Escribiendo el cuadrado como producto.
= x.(x + 3) + 3 ( x + 3)
Distribuyendo.
= x
2
+ 3x + 3x + 9 Distribuyendo nuevamente.
= x
2
+6x + 9 Asociando y sumando los términos
semejantes.
De este modo podemos reemplazar a x
2
+ 6x + 9 por la expresión (x + 3)
2
en la ecuación
dada y escribir:
x
2
+ 6x + 9 = 4
(x +3)
2
= 4
Y se resuelve en forma análoga al ejemplo 5.
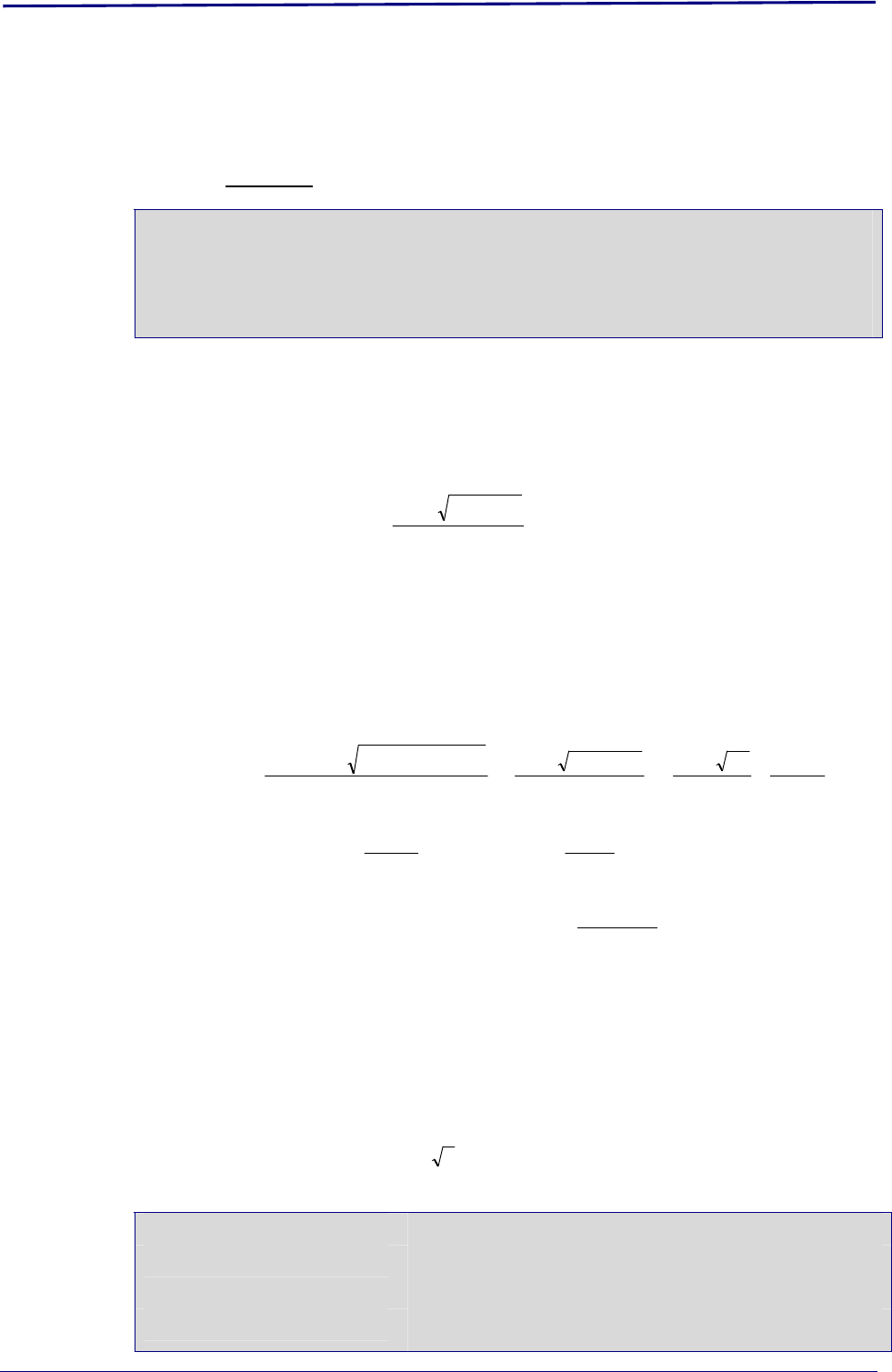
5xó1-xdondede
2-3xó23x
23x
4)3x(
2
UBA XXI Modalidad virtual
Matemática
UBA XXI – MÁTEMATICA - Ecuaciones e Inecuaciones 4
Si se reemplazan estos valores en la ecuación dada, se ve que son solución.
Para x = -1 es (-1)
2
+(-1).6 + 9 = 1 – 6 + 9 = 4
Para x = -5 es (-5)
2
+ (-5).6 + 9 = 25 –30 + 9 = 4
Entonces S = {-5; -1}
El procedimiento usado se basa en las propiedades trabajadas en el anexo de números
reales:
(m + n)
2
= m
2
+ 2mn+ n
2
(m - n)
2
= m
2
- 2mn + n
2
Otras ecuaciones de segundo grado no pueden reducirse a ninguno de los casos
anteriores. Por ejemplo
2x
2
–12 x + 10 = 0
Para resolverlas utilizamos la fórmula
a2
ac4bb
x
2
2,1
donde a es el coeficiente de x
2
; b es el coeficiente del término lineal x y c es el término
independiente y x
1,2
son las posibles soluciones de la ecuación dada.
Ejemplo 7. Resolver la ecuación 2x
2
–12 x + 10 = 0
Solución:
Teniendo en cuenta que a = 2; b = -12 y c = 10 reemplazamos en la fórmula anterior:
1
4
8-12
x5
4
812
xesEntonces
4
812
4
6412
4
8014412
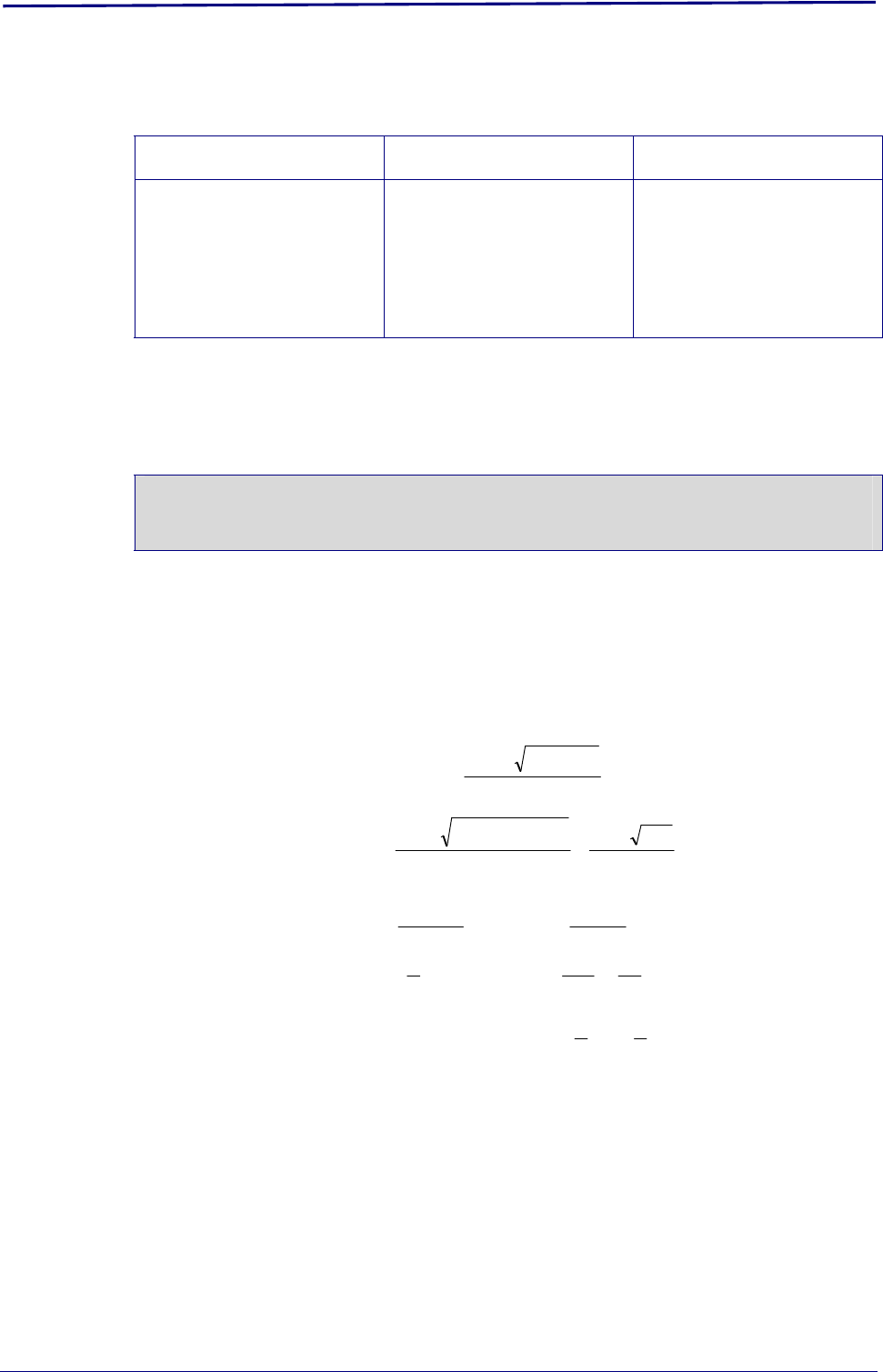
2.2
10.2.4)12()12(
x
21
2
2,1
Así el conjunto de soluciones de la ecuación dada es S = { 1; 5} lo que puede verificarse
Número de soluciones de una ecuación de segundo grado
Según los ejemplos tratados, una ecuación de segundo grado puede tener una, dos o
ninguna solución.
Al trabajar con la fórmula resolvente, este hecho puede conocerse analizando el radicando
b
2
– 4ac, llamado discriminante.
Luego, teniendo en cuenta que z está definida en los reales sólo cuando z
0,
analicemos el discriminante b
2
– 4ac.
• Si b
2
– 4ac > 0 la ecuación tiene dos soluciones reales y distintas.
• Si b
2
– 4ac = 0 la ecuación tiene una sola solución real.
Diremos que es una raíz doble o de multiplicidad 2.
• Si b
2
– 4ac < 0 la ecuación no tiene soluciones reales.
UBA XXI Modalidad virtual
Matemática
UBA XXI – MÁTEMATICA - Ecuaciones e Inecuaciones 5
Ejemplo 8. Analizamos el discriminante en cada uno de los siguientes casos
2x
2
– 8x + 6 = 0 x
2
+ 6x + 9 = 0 3x
2
+2x + 1 = 0
b
2
– 4ac = (-8)
2
–4.2.6 = 16
Como el discriminante
es mayor que 0 se
puede afirmar que la
ecuación tiene dos
soluciones reales.
b
2
– 4ac = 6
2
– 4.1.9 = 0
Como el discriminante
es igual a 0 se puede
afirmar que la ecuación
tiene una raíz doble o
de multiplicidad 2.
b
2
– 4ac = 2
2
–4.3. 1 = -8
Como el discriminante
es menor que 0 se
puede afirmar que la
ecuación no tiene
soluciones reales.
Expresión como producto de una ecuación de segundo grado
conocidas sus raíces.
Si x
1
y x
2
son las raíces de la ecuación ax
2
+ bx + c = 0 entonces es:
ax
2
+ bx + c = a(x - x
1
) ( x - x
2
)
Ejemplo 9. Expresar como producto 2x
2
+ 5x –18
Solución
Para poder escribir como producto la expresión se deben hallar las raíces de
2x
2
+ 5x –18 = 0.
Aplicando la fórmula resolvente
a2
ac4bb
x
2
2,1
para a = 2; b = 5 y c = -18:
2
9-
4
18-
x
4
9
x
4
13-5-
x
4
135
x
esEntonces
4
1695-
2.2
)18.(2.455
x
21
21
2
2
,1
Así
2
9
x
4
9
x218-5x2x
2

UBA XXI Modalidad virtual
Matemática
UBA XXI – MÁTEMATICA - Ecuaciones e Inecuaciones 6
Otros tipos
de
ecuaciones
En general, para resolver ecuaciones de otro tipo, no están al alcance de este curso o no
se dispone de fórmulas que permitan hallar las soluciones.
Por ejemplo la ecuación de tercer grado
2x
3
- 5x
2
–x + 6 = 0.
Pero si nos dan la misma ecuación en forma factorizada
(2x -3) (x+1) (x - 2) = 0
podemos usar una propiedad que ya hemos usado: si un producto es cero alguno de los
factores es cero.
De este modo llegamos, rápidamente a las soluciones:
2x1x
2
3
x
321
Conviene tener en cuenta que cuando nos dan la ecuación factorizada y queremos hallar
sus raíces, no es conveniente desarrollar los productos.
Ejemplo 10. Resolver la ecuación (x – 5) (x
2
– 4) (x +1) = 0
Solución
Si desarrollamos el producto, aplicando sucesivamente propiedad distributiva de la
multiplicación respecto a la suma, tenemos:
x
4
– 4x
3
– 9x
2
-16x + 20 = 0
llegamos a una expresión que no podríamos resolver con los conocimientos que tenemos.
Pero sí podemos resolver
(x – 5) (x
2
– 4) (x +1) = 0
igualando cada uno de los factores a cero. Es decir
x – 5 = 0 x
2
– 4 = 0 x + 1 = 0
De donde es x
1
= 5 x
2
= 2 x
3
= -2 x
4
= -1
(Observamos que x
2
– 4 = 0 tiene por soluciones a 2 y a -2)
Luego S = { -2; -2: 2; 5}
La ecuación resuelta en el ejemplo es una ecuación de cuarto grado, que tiene todos sus
términos.
Ecuaciones
bicuadradas
Otras ecuaciones de cuarto grado tienen un aspecto similar a las de segundo grado. Son
las llamadas ecuaciones bicuadradas. Su expresión general es:
ax
4
+ bx
2
+ c = 0 con a 0.
Para resolverlas, comenzamos por escribirlas en la forma:
ax
4
+ bx
2
+ c = a(x
2
)
2
+ bx
2
+ c = 0
Y haciendo la sustitución x
2
= z, la expresión anterior queda:
az
2
+ bz + c = 0
que es una ecuación de segundo grado con incógnita z.

UBA XXI Modalidad virtual
Matemática
UBA XXI – MÁTEMATICA - Ecuaciones e Inecuaciones 7
Ejemplo 11. Resolver la ecuación 4x
4
–5x
2
+ 1 = 0
Solución
Reemplazando x
2
por z, nos queda
4z
2
– 5z +1 = 0.
Resolvemos para la variable z, usando la fórmula resolvente (siendo a = 4; b = -5 y c = 1)
4
1
z1z
8
35
z
8
35
z
esmodoesteDe
8
35
8
16-255
4.2
1.4.4)5()5(
z
21
21
2
2,1
Los dos valores hallados son solución de la ecuación 4z
2
– 5z +1 = 0.
Ahora debemos obtener los valores de x (ya que hicimos la sustitución x
2
= z)
Para z
1
= 1 es x
2
= 1 1-xó1x1x11x
2
Para
2
1
-xó
2
1
x
2
1
x
4
1
x
4
1
xes
4
1
z
22
2
Entonces el conjunto solución de 4x
4
–5x
2
+ 1 = 0 es
1;
2
1
;
2
1
;1S
Ecuaciones
con radicales
En ocasiones la variable aparece bajo un radical. Sólo consideraremos el caso en que
este sea una raíz cuadrada.
Para resolverlas se debe elevar al cuadrado a ambos miembros para obtener una
ecuación sin raíces cuadradas, pero esto no nos conduce a ecuaciones equivalentes por
lo que las soluciones que hallemos deben ser comprobadas necesariamente en la
ecuación dada.
Ejemplo 12. Resolver 52x
3
Como la raíz cuadrada está definida sólo cuando el radicando es mayor o igual que cero,
lo primero que vemos es cuál es el dominio de definición de esta ecuación.
Buscamos para qué números reales es x
3
- 2 0 y encontramos que debe ser
3
2x .
Esto quiere decir que si encontramos algún resultado que no cumpla esta condición, el
mismo no es solución de la ecuación dada.
Resolvemos:
52x
3
252x
52x
3
2
2
3
Elevamos ambos miembros al cuadrado y
teniendo en cuenta el dominio de
definición operamos.

UBA XXI Modalidad virtual
Matemática
UBA XXI – MÁTEMATICA - Ecuaciones e Inecuaciones 8
x
3
- 2 + 2 = 25 + 2
x
3
= 27
3
3
3
27x
x = 3
Sumamos 2 a ambos miembros
Sacamos raíz cúbica en ambos miembros
Como x = 3 cumple la condición de ser mayor o igual que
3
2 , entonces la solución de la
ecuación es S = {3}
Conviene verificarlo en la ecuación original 52x
3
.
Ecuaciones
con
expresiones
racionales
Las ecuaciones racionales son aquellas expresadas como fracciones u operaciones entre
fracciones en las que la incógnita está en el denominador.
Habitualmente se procura transformarlas mediante operaciones algebraicas en otra
ecuación que sea más fácil de resolver y que tenga las mismas soluciones de la dada.
Ejemplo 12. Hallar las soluciones de la ecuación
2x
2
1x
4
2x
x
Solución
Al estar la incógnita en los denominadores, buscamos el dominio de definición de la
ecuación. En este caso, debemos ver para qué valores se anulan (ya que no podemos
dividir por cero).
Vemos que x + 1 = 0 si x = -1 y x + 2 = 0 si x = -2.
Luego, el dominio de definición de la ecuación son todos los números reales distintos de
-2 y de -1.
2x
2
1x
4
2x
x
0
2x
2
1x
4
2x
x
Igualamos a cero
Para operar en el primer miembro, buscamos común denominador:
0
)1x()2x(
)1x(2)2x(4)1x(x
0
)1x()2x(
6xx
0
)1x()2x(
2x28x4xx
2
2
Y operamos
x
2
–x – 6 = 0 Multiplicamos ambos miembros por
(x+2)(x+1) (esto podemos hacerlo
porque estamos trabajando para x
-2 y x -1)
Logramos escribir la ecuación dada como una ecuación de segundo grado. La
resolvemos utilizando la fórmula
a2
ac4bb
x
2
2,1
En la ecuación resultante es a = 1; b = -1 y c = -6. Luego:
2
51
2
2411
2
)6.(1.4)1()1(
x
2
2,1

UBA XXI Modalidad virtual
Matemática
UBA XXI – MÁTEMATICA - Ecuaciones e Inecuaciones 9
Con lo que es:
2
2
51
xy3
2
51
x
21
Llegados aquí, podemos tentarnos y decir que estas son las soluciones de la ecuación
dada.
Pero si lo hacemos cometeríamos un error ya que x = -2 no pertenece al dominio de
definición de la función.
Entonces la única solución es x = 3.
S = {3}
Observación: Muchas veces al hacer transformaciones en una ecuación para escribirla
de manera equivalente, aparecen soluciones extrañas o se pierden algunas. Por ello,
siempre debemos verificar si los valores obtenidos son realmente las soluciones de la
ecuación dada.
UBA XXI Modalidad virtual
Matemática
UBA XXI – MÁTEMATICA - Ecuaciones e Inecuaciones 10
Inecuaciones Al igual que con las ecuaciones, ampliamos ahora nuestro estudio a ecuaciones no lineales
con una incógnita.
En su resolución, usamos propiedades de los números reales, incorporamos el uso de los
intervalos y de valor absoluto.
Lo haremos mediante ejemplos.
Ejemplo 1.
Resolver (x – 1)(x +3) > 0
Solución
En el primer miembro de la desigualdad tenemos un producto de
números reales.
Para que el producto sea mayor que cero deben ser ambos factores
positivos o ambos negativos. Planteamos:
a. b > 0
a >0 b > 0
a<0 b < 0
x – 1 > 0 x +3 > 0 x – 1 < 0 x +3 < 0
Y resolvemos las inecuaciones que nos quedaron
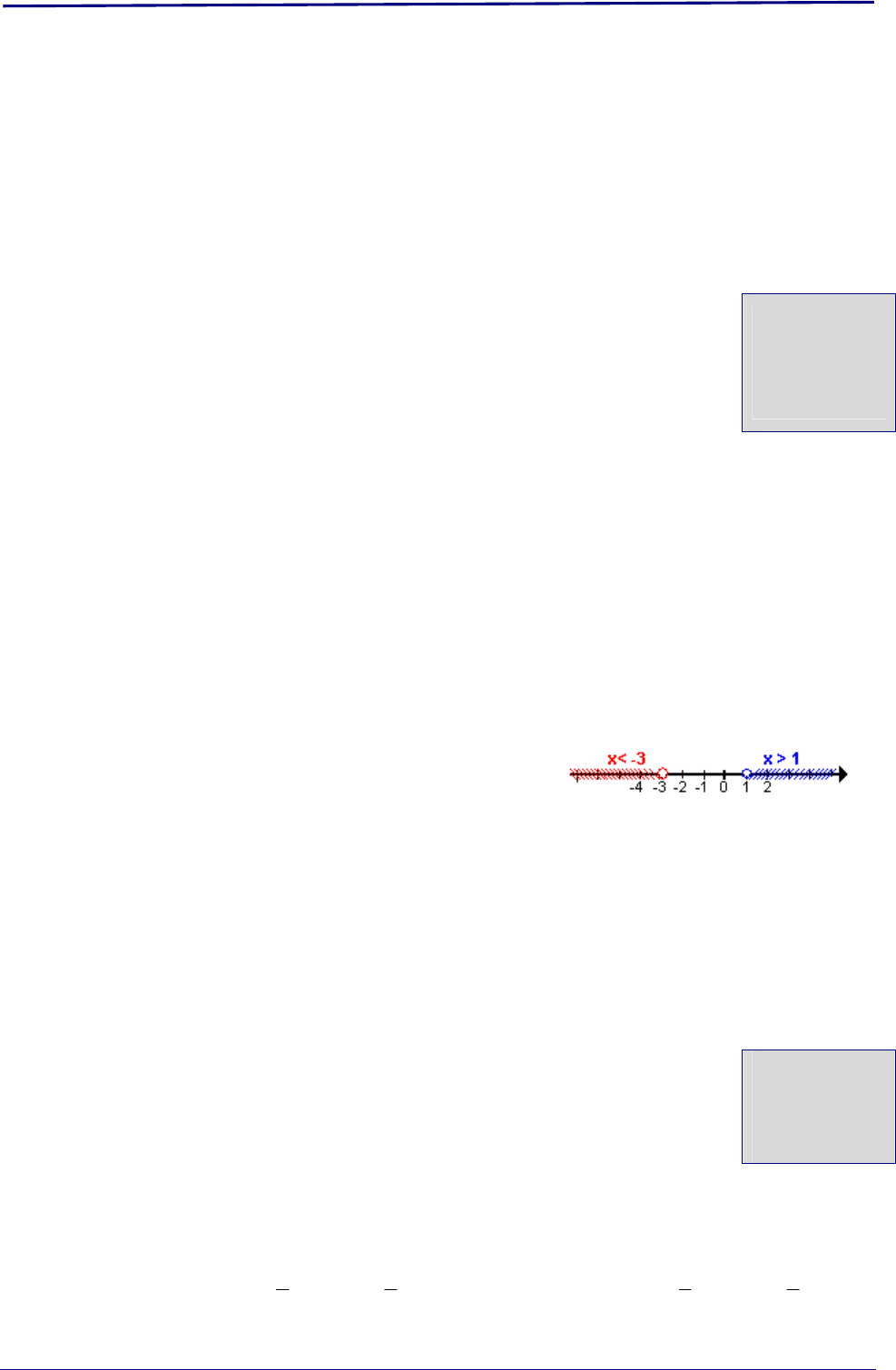
x > 1 x > - 3 x < 1 x < - 3
Los números que buscamos tienen que
cumplir al mismo tiempo ser mayores que
-3 y mayores que 1.
Esto ocurre si es x > 1
Los números que buscamos tienen que
cumplir al mismo tiempo ser menores que
-3 y menores que 1.
Esto ocurre si es x < -3
Encontramos las soluciones parciales:
S
1
= (1; +) S
2
= (-; -3)
Hallamos el conjunto solución como unión
de intervalos
S = (1; +) (-; -3)
Como los intervalos no tienen elementos en
común esta es la solución.
Ejemplo 2. Resolver 4x
2
< 25
Solución
Escribimos la inecuación de la siguiente manera:
4x
2
- 25 < 0
Como 4x
2
– 25 = (2x + 5 ) (2x – 5), reemplazamos
(2x + 5 ) (2x – 5)< 0
Así en el primer miembro de la desigualdad tenemos un producto de
números reales.
Y para que el producto sea menor que cero debe ser uno de los factores
mayor que cero y el otro menor que cero. Planteamos:
a. b < 0
a >0 b < 0
a < 0 b > 0
2x + 5 > 0 2x – 5 < 0 2x + 5 < 0 2x – 5 > 0
Y resolvemos las inecuaciones que nos quedaron
2
5
x
2
5
x
5x25x2
2
5
x
2
5
x
5x25x2

UBA XXI Modalidad virtual
Matemática
UBA XXI – MÁTEMATICA - Ecuaciones e Inecuaciones 11
Encontramos las soluciones parciales
2
5
;
2
5
S
1
S
2
=
Hallamos el conjunto solución como unión de intervalos
2
5
;
2
5
S
2
5
;
2
5
SSS
21
Ejemplo 3. Sea A = {x/x(x
2
– 1) 0}
Representar A en la recta numérica y escribirlo como intervalo o unión de
intervalos.
Solución
Para representar al conjunto A en la recta numérica y escribirlo como intervalo o unión de
intervalos, debemos encontrar los elementos de A.
Todos los números que pertenecen a este conjunto cumplen la condición 2x(x
2
– 4 0.
Por lo que, para encontrar los elementos de A, hay que hallar la solución de la inecuación.
Tenemos en cuenta que el producto entre dos factores es mayor o igual que cero cuando
ambos son mayores o iguales que cero o bien cuando ambos son menores o iguales que
cero.
Planteamos
x(x
2
– 1) 0
x 0 x
2
– 1 0 x 0 x
2
– 1 0
Y resolvemos las inecuaciones que nos quedaron
x 0 x
2
1 x 0 x
2
1
x 0 1x
2
x 0 1x
2
Teniendo en cuenta que xx
2
, escribimos
x 0 1x
x 0 1x
En ambos miembros tenemos una expresión con módulo. Usando propiedades es:
|x| 1 x 1 x -1
|x| 1 -1 x 1
Reemplazamos
x 0 (x 1 x -1) x 0 ( -1 x 1)
Nos ayudamos con un gráfico para hallar las soluciones parciales y las escribimos como
intervalos.
Los puntos de la recta doblemente rayados son, en cada caso, la solución Escribimos:

UBA XXI Modalidad virtual
Matemática
UBA XXI – MÁTEMATICA - Ecuaciones e Inecuaciones 12
S
1
= [1; +)
0;1S
2
Hallamos el conjunto solución como unión de los dos anteriores.
0;1;1S
SSS
21
Ejemplo 4. Escribi cada conjunto como intervalos o unión de intervalos.
a)
1
2x
1x2
/xM
b)
0
1x
5
/xQ
Solución
En todos los ejercicios, la condición que cumplen sus elementos está expresada por un
cociente. Las propiedades que se utilizan para resolver la inecuación son similares a las
del producto.
a)
1
2x
1x2
/xM Como no podemos dividir por cero, los elementos de M
serán números reales distintos de 2.
Debemos resolver la inecuación 1
2x
1x2
.
La escribimos la inecuación en forma equivalente restando miembro a miembro 1.
01
2x
1x2
111
2x
1x2
Y operamos:
0
2x
3x
0
2x
2x1x2
0
2x
)2x()1x2(
De este modo, podemos comparar la inecuación con cero. Recordamos además que para
que un cociente sea menor que cero deben ser numerador y denominador de signos
distintos.
Planteamos:
x + 3 > 0 x – 2 < 0 x + 3 < 0 x – 2 > 0
Resolvemos las inecuaciones y buscamos las soluciones parciales
x > -3 x < 2 x < -3 x > 2
Los números reales que son a la vez
mayores que -3 y menores que 2
pertenecen al intervalo (-3; 2)
S
1 =
(-3; 2)
No hay ningún número real que sea a la
vez menor que -3 y mayor que 2
S
2
=

UBA XXI Modalidad virtual
Matemática
UBA XXI – MÁTEMATICA - Ecuaciones e Inecuaciones 13
Y damos la solución S = S
1
S
2
S = (-3; 2)
Como 2 (que no pertenece al dominio de M) , no pertenece al intervalo (-3; 2) entonces es
S = (-3; 2)
b)
0
1x
5
/xQ
Solución
Como no podemos dividir por cero, los elementos de Q, son todos los números reales
distintos de 1.
Además, para que
1x
5
sea mayor que cero, deben ser el numerador y el denominador,
los dos mayores que cero o los dos menores que cero.
Como
5 > 0 siempre
|x – 1| > 0 para todo número real (por definición de módulo)
el numerador y el denominador son siempre positivos.
Entonces
1x
5
es mayor que cero para todo número real distinto de 1.
Y S = - {1}
5. Aplicaciones de la derivada 1.pdf
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.