
UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 28
Superficies cuádricas
INTRODUCCIÓN
Hemos realizado el estudio del plano como la más elemental de las superficies, cuya ecuación
es:
Ax + By + Cz +D= 0
A continuación nos dedicaremos al estudio de las superficies en general, las que
analíticamente responden a la forma F(x, y, z) =0 ecuación con tres variables referida a un
sistema coordenado rectangular.
Es conveniente destacar que no es necesaria la existencia de las tres variables para que la
ecuación represente una superficie, por ejemplo x = 3 es un plano paralelo al plano
coordenado yz. Por otra parte, toda ecuación con tres variables no representa una superficie,
tal es el caso de:
0
222
zyx
que solo se satisface para el origen de coordenadas P (0,
0, 0).Ya hemos estudiado que en el caso en que F (x, y, z) = 0 sea una ecuación de primer
grado, la superficie que le corresponde es un plano. Estudiaremos ahora los casos en que en
que las ecuaciones F (x, y, z) = 0 sean de grado superior a uno y por consiguiente se
obtendrán superficies no planas.
Dada la ecuación de una superficie, se acostumbra hacer una discusión previa en algunos
puntos con vista a valernos de los resultados de dicho estudio para representar gráficamente la
superficie.
DISCUSION Y TRAZADO DE UNA SUPERFICIE
Para trazar una superficie nos basaremos en los siguientes puntos:
1- Interceptos con los ejes coordenados.
2- Trazas sobre los planos coordenados.
3- Simetría respecto a los planos coordenados, ejes coordenados y origen.
4- Secciones planas paralelas a los planos coordenados.
5- Extensión.
6- Representación gráfica.
Ilustraremos la discusión de los puntos anteriores con un ejemplo específico
.
Trazar la gráfica de la superficie:
4x
2
+ y
2
+ 9z
2
= 36

UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 29
1- INTERSECCION CON LOS EJES COORDENADOS
Hemos visto que los puntos sobre los ejes coordenados tienen dos coordenadas nulas y una
diferente de cero. (exceptuando el origen de coordenadas). Luego, si la superficie intercepta
los ejes coordenados, los puntos de intersección cumplirán las características descriptas arriba,
así saber si la superficie intercepta al eje x, hacemos y = 0 y z = 0 en su ecuación, de tener x
un valor real, ese será el punto de intersección. Similarmente se hace con los restantes ejes
coordenados.
En nuestro caso:
a- Interceptos con el eje x.
y0 , z0
4x
2
= 36 x
2
= 9 x =
3
Tenemos dos intersecciones (3, 0, 0) y (-3, 0, 0)
b- Interceptos con el eje y.
x 0 ; z 0
y
2
= 36 y =
6
Tenemos dos intersecciones (0, 6, 0) y (0, -6, 0)
c- Intersecciones con el eje z.
x 0 y y=0
9z
2
= 36 z
2
=
9
36
z
2
= 4 z =
2
Tenemos dos intersecciones (0, 0, 2) y (0, 0, -2)
2- TRAZAS SOBRE LOS PLANOS COORDENADOS
Anteriormente hicimos uso del concepto de traza de un plano cualquiera con uso de los planos
coordenados, similarmente la traza de una superficie sobre un plano coordenado es la curva de
intersección de la superficie con el plano en cuestión. Su expresión analítica está dada por la
consideración simultánea de las ecuaciones de la superficie y el plano coordenado.
Para nuestro ejemplo: 4x
2
+ y
2
+ 9z
2
= 36 tenemos:
a- La traza sobre el plano xy es:
0
364
22
z
yx
Que puede ser expresada en la forma:
0
1
369
22
z
yx
Representando sobre el plano xy una elipse
cuyos semiejes son a = 3 y b = 6, teniendo
como centro el origen de coordenadas.
Su representación gráfica es la siguiente:
x
y
z
(0,-6,0) (0,6,0)
(-3,0,0)
(3,0,0)

UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 30
b- La traza sobre el plano xz es :
0
3694
22
y
zx
que también se expresa como :
0
1
49
22
y
zx
Representando sobre el plano xz una elipse cuyos semiejes son a = 3 y c = 2, teniendo como
centro al origen de coordenadas.
Su representación gráfica es:
c- La traza sobre el plano yz es :
0
369
22
x
zy
o lo que es lo mismo
0
1
436
22
x
zy
Elipse en el plano yz, de semiejes b = 6 y c = 2 y con centro en el origen de coordenadas.
Gráficamente la traza queda:
z
x
y
(-3,0,0)
(3,0,0)
(0,0,2)
(0,0,-2)
z
x
y
(0,6,0)
(0,-6,0)
(0,0,2)
(0,0,-2)

UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 31
Obsérvese que en la determinación de las trazas, se identifica la curva plana que se produce en
el plano coordenado, se representa gráficamente y se verifica la coincidencia de los puntos de
intersección de la curva con los interceptos de la superficie sobre los ejes coordenados, tal y
como hemos hecho en este ejemplo.
3- SIMETRIA
a- Respecto a los planos coordenados
El punto simétrico de P (x, y, z) respecto al plano xy tiene la misma abscisa y ordenada que P
y su cota es igual pero de signo contrario.
Si la superficie pasa por P (x, y, z), sus coordenadas son raíces de la ecuación de la misma, y
si ella fuese simétrica respecto al plano xy, pasará por P' (x, y, -z), y las coordenadas de este
punto también serían raíces de la ecuación de la superficie.
Al hacer la sustitución de las variables de la ecuación F (x, y, z) = 0 por las coordenadas de P'
(x, y, -z), lo único que cambiamos es la z por -z. Luego para averiguar si la superficie es
simétrica respecto al plano xy, sustituimos en su ecuación la z por -z, si la ecuación no se
altera, hay simetría. Gráficamente:
Similarmente, para probar la simetría respecto al plano yz, sustituimos x por -x, y para el
plano xz sustituimos y por -y.
En nuestro ejemplo: 4x
2
+ y
2
+ 9z
2
= 36 hay simetría respecto a los tres planos coordenados,
puesto que las variables aparecen elevadas al cuadrado y los cambios sucesivos de x por -x, y
por -y, z por -z no se alteran.
b- Respecto a los ejes coordenados
Eje x
Para establecer la prueba de la simetría de una superficie respecto a un eje coordenado,
hallaremos primeramente la relación que existe entre las coordenadas de un punto P y su
simétrico P' respecto al eje coordenado x, trazamos por P (x, y, z ) un plano perpendicular
al eje x, el cuál determinará sobre éste un punto A. Unamos P con A mediante una recta y en
su prolongación a una distancia igual a PA, situemos el punto P' de manera que PA = AP'. El
punto P' será entonces simétrico del punto P respecto al eje x.
Gráficamente
z
x
y
O
P (x,y,z)
P’(x,y,-z)

UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 32
De la figura es fácil comprobar la igualdad de los triángulos PMA y P'M'A', de manera que si
las coordenadas de P son (x, y, z), entonces las coordenadas de M son (x, y, 0), las de M'
son (x, -y, 0) y las de P' son (x, -
y
, -z).
Por lo tanto, las coordenadas de un punto P' simétrico a un punto P (x, y, z) respecto al eje x
son (x, -y, -z), donde cambian de signo la ordenada y la cota, manteniéndose el signo de la
abscisa que es la variable que se mide a lo largo del eje sobre el cual se prueba la simetría.
Entonces, si tenemos una superficie que pasa por el punto P (x, y, z ) y es simétrico respecto
al eje x pasará también por el punto P' (x, -
y
, -z ) cuyas coordenadas satisfacen la
ecuación de la misma. Luego, para saber si una superficie es simétrica respecto al eje x,
sustituimos y por -y y z por -z, si su ecuación no se altera, es simétrica respecto a ese eje.
En nuestro ejemplo: 4x
2
+ y
2
+ 9 z
2
= 36 se comprueba que tales sustituciones no alteran la
ecuación.
4x
2
+ (-y)
2
+ 9 (-z)
2
= 36 es la misma que: 4x
2
+ y
2
+ 9z
2
= 36
Por lo que hay simetría en el eje x.
Eje y:
Por un razonamiento similar al anterior, la simetría de una superficie respecto al eje y, se
comprueba si al sustituir en la ecuación de la misma x por -x y z por -z no se altera la
ecuación.
Luego, se sabe claramente que la superficie que estamos estudiando es simétrica respecto al
eje y.
4(-x)
2
+ y
2
+ 9 (-z)
2
= 36 es la misma ecuación que: 4x
2
+ y
2
+ 9z
2
= 36
Eje z:
La simetría de una superficie respecto al eje z se comprueba si al sustituir en la ecuación de la
misma x por -x e y por -y ésta no se altera.
La superficie en estudio es también simétrica respecto al eje z, ya que:
4(-x)
2
+(-y)
2
+ 9 z
2
= 36 es la misma que: 4x
2
+ y
2
+ 9z
2
= 36
A
z
x
y
M(x,y,0)
O
P (x,y,z)
P’(x,-y,-z)
M’(x,-y,0)

UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 33
c. Respecto al origen
Si dos puntos son simétricos respecto a los tres planos coordenados, será también simétrico
respecto al origen. Vimos que, para hallar la simetría respecto a los planos coordenados,
cambiamos de signo sucesivamente a las variables, luego si este cambio se realiza
simultáneamente se obtendrán las coordenadas de un punto simétrico a otro respecto al
origen. Es decir, las coordenadas de un punto simétrico a P (x, y, z) respecto al origen son
(-x, -y, -z).
Por tanto, una superficie será simétrica respecto al origen de coordenadas, si al sustituir
simultáneamente en su ecuación x por –x, y por -y y z por -z la misma no se altera.
En el ejemplo que estamos estudiando, la superficie es simétrica respecto al origen, ya que:
4(-x)
2
+ (-y)
2
+ 9 (-z)
2
= 36 es lo mismo que 4x
2
+ y
2
+ 9z
2
= 36
4- SECCIONES PLANAS PARALELAS A LOS PLANOS COORDENADOS
El hecho de que la superficie se desarrolla en el espacio tridimensional, hace que nos baste
con la información de los elementos que hemos discutido hasta aquí. Las secciones planas
determinadas por planos paralelos a los planos coordenados nos permiten conocer, analizando
las curvas de intersección de la superficie con cada uno de esos planos, la configuración de la
misma en el espacio.
Los planos paralelos a los planos coordenados, tienen en general, ecuaciones de la forma:
1
kx
, los paralelos al plano
yz
2
ky
, los paralelos al plano
xz
3
kz
, los paralelos al plano
xy
Las curvas de intersección con estos planos se obtienen haciendo las sustituciones
1
kx
,
2
ky
,
3
kz
, sucesivamente en la ecuación de la superficie e identificando dichas curvas.
Las secciones planas las utilizaremos también para definir la extensión de la superficie.
En la superficie
3694
222
zyx
, las secciones planas paralelas al plano
yz
se obtienen
haciendo
kx
.
kx
kzy
222
4369
Estas curvas serán elipses siempre que:
2
436 k
0 de donde 36
2
4k
o lo que es lo mismo
2
k
9
k
3 finalmente -3
k
3
Es decir, que podemos cortar la superficie por planos paralelos al plano
yz
desde el punto (-3,
0, 0) al (3, 0, 0) y las curvas de intersección en estos planos son elipses.
Las secciones planas paralelas al plano
xz
, se hallan haciendo
ky
.
ky
kzx
222
3694
Estas curvas serán elipses siempre que:
2
36 k
0
o sea -6
k
6

UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 34
Para las secciones planas paralelas al xy se sustituye z=k y se obtiene:
kz
kyx
222
9364
Estas curvas serán elipses siempre que:
0936
2
k
es decir -2
k
2
5- EXTENSIÓN
En este punto nos proponemos estudiar la localización general de la superficie en el espacio
coordenado, indicando si la misma es cerrada o indefinida en extensión. La base de la
extensión de una superficie está dada en el estudio realizado en las secciones planas paralelas
a los planos coordenados, ya que en ella establecimos claramente los intervalos de variación
de los valores reales que las variables pueden tomar.
En nuestro ejemplo, las secciones planas están limitadas sobre cada eje por intervalos situados
entre los respectivos interceptos de la superficie con dichos ejes, por tanto, concluimos que la
superficie es CERRADA.
6- REPRESENTACION GRAFICA
Esta superficie se denomina elipsoide, y en el transcurso de esta unidad la estudiaremos con
más detalles.
Generalmente se suele representar sólo la porción de superficie comprendida en el primer
octante, en tal caso se dibujan las partes de las trazas que contengan los interceptos positivos;
así para el elipsoide en estudio quedaría.
z
x
y
O
z
x
y
O
3
6
2

UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 35
ECUACION GENERAL DE 2°GRADO EN EL ESPACIO
SUPERFICIES CUADRICAS
De considerable importancia en la geometría analítica de tres dimensiones es la ecuación
general de segundo grado con tres variables.
0
222
KIzHyGxFyzExzDxyCzByAx
Donde uno, por lo menos, de los coeficientes de los términos de segundo grado, es diferente
de cero.
Llamaremos SUPERFICIES CUADRICAS o simplemente CUADRICAS, a toda superficie
cuya ecuación sea de segundo grado.
Es obvio que la ecuación dada, por ser una ecuación general no es lo suficientemente sencilla
como para estudiar las propiedades geométricas de la superficie que ella representa, pero
sabemos también que esta superficie no se altera si nosotros, mediante una transformación de
coordenadas, llevamos la ecuación a una forma algebraica más simple, dejamos sin términos
rectangulares
,,, xzyzxy
que se suprimen por rotación de ejes, y sin términos de 1° grado que
eliminaremos mediante una traslación de ejes coordenados.
En los problemas de transformación de coordenadas, llegábamos a simplificar las ecuaciones
hasta que tuvieran solo términos cuadrados, o hasta que quedaran con un término cuadrado y
uno de primer grado (parábola). Es decir, se llegaba a dos tipos de ecuaciones:
0
22
FByAx
(circunferencias, elipses, o hipérbolas)
0
2
ByAx
(parábolas)
Generalizando para una tercera dimensión, cuando hallemos la transformación de
coordenadas, obtendremos dos tipos de ecuaciones, una que tendrá solamente los términos
cuadrados y un término independiente de las variables, cuya forma general es:
RPzNyMx
222
(1)
y otra en la que aparecerán dos variables al cuadrado y una lineal y que podemos escribir.
SzNyMx
22
(2)
La ecuación (1), por razones geométricas, es la ecuación de las CUADRICAS CON CENTRO
O CENTRADAS y la ecuación (2), la de las CUADRICAS SIN CENTRO O NO
CENTRADAS.
CUADRICAS CENTRADAS:
Analicemos la ecuación:
RPzNyMx
222
Comencemos suponiendo
0R
A- Si los tres coeficientes:
0,0,0 PyNM
Dividimos toda la ecuación por R:

UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 36
R
Mx
2
+
R
Ny
2
+
R
Pz
2
R
R
Y llevemos los coeficientes de las variables, al denominador:
M
R
x
2
+
N
R
y
2
+
P
R
z
2
1
Puesto que todos los parámetros (M, N, P y R) son positivos hagamos la siguiente sustitución
.
2
a
M
R
;
2
b
N
R
;
2
c
P
R
Y la ecuación queda:
1
2
2
2
2
2
2
c
z
b
y
a
x
Se puede comprobar que esta superficie corta a los ejes coordenados en
ooa ,,
,
obo ,,
y
coo ,,
; que es simétrica respecto al origen, los ejes y los planos
coordenados, que es cerrada y que además todas sus secciones planas paralelas a los planos
coordenados (incluyendo las trazas) son elipses. Su nombre es ELIPSOIDE; con centro en el
origen de coordenadas y cuya ecuación en forma canónica es la obtenida anteriormente.
La representación gráfica del elipsoide se muestra a continuación:
Es decir, que directamente podemos identificar cualquier ecuación de 2° grado que cumpla las
condiciones dadas, como la de un elipsoide y representarla gráficamente sin necesidad de
hacer la discusión de la superficie. Generalmente la representación gráfica se limita
exclusivamente al primer octante.
Ejemplo: Representar gráficamente el elipsoide cuya ecuación es:
3694
222
zyx
Para realizar la representación del elipsoide, debemos llevar su ecuación a la forma canónica,
la cual se logra dividiendo toda la ecuación por el término independiente.
1
3649
222
zyx
De ella podemos obtener los interceptos del elipsoide con los ejes coordenados.
3a
;
2b
;
6c

UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 37
Y hacer la representación gráfica directamente.
Casos particulares
Si en la ecuación:
1
2
2
2
2
2
2
c
z
b
y
a
x
cba
, el elipsoide es achatado (figura 1)
Si
cba
, el elipsoide es alargado. (Figura2)
Si
cba
, obtenemos la esfera de radio
ar
(Figura 3)
La ecuación:
1
2
2
2
2
2
2
c
z
b
y
a
x
Se transforma:
1
2
2
2
2
2
2
a
z
a
y
a
x
o sea
2222
azyx
Que es la ecuación de la esfera con centro en el origen y radio a.
z
x
y
O
(3,0,0)
(0,2,0)
(0,0,6)
z
x
y
O
(a,0,0)
(0,b,0)
(0,0,c)
z
x
y
O
(a,0,0)
(0,a,0)
(0,0,a)
z
x
y
O
(a,0,0)
(0,b,0)
(0,0,c)
Figura 1
Figura 2 Figura 3
UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 38
B- En el caso en que las ecuaciones
RPzNyMx
222
Dos coeficientes sean positivos y uno negativo; o sea:
000 PyNM
la ecuación queda:
1
222
z
R
P
y
R
N
x
R
M
ordenando
1
222
P
R
z
N
R
y
M
R
x
pero estudiando a los signos de los coeficientes M, N , P y R, hagamos la siguiente
sustitución.
2
a
M
R
;
22
; c
P
R
b
N
R
por lo que la ecuación queda:
1
2
2
2
2
2
2
c
z
b
y
a
x
Esta superficie corta a los ejes x e y en los puntos
ooa ,,
y
obo ,,
respectivamente, es
simétrica respecto al origen, los ejes y los planos coordenados, es abierta puesto que las tres
variables pueden tener cualquier valor real, secciones planas paralelas al plano xy dan como
resultado elipses, mientras que secciones planas paralelas a los otros planos coordenados dan
hipérbolas. Su nombre es HIPERBOLOIDE DE UNA HOJA. Y su eje es el de igual
denominación a la variable que aparezca con signo negativo, en este caso el eje z.
Otras formas canónicas de la ecuación de un hiperboloide de una hoja pueden ser:
11
2
2
2
2
2
2
2
2
2
2
2
2
c
z
b
y
a
x
c
z
b
y
a
x
Las cuales representan superficies con características similares a las analizadas anteriormente,
pero teniendo en cuenta que los ejes de las figuras en este caso son el eje y y el eje x
respectivamente.
Ejemplo: Representar, en el 1° octante, el hiperboloide de una hoja cuya ecuación es:
3649
222
zyx
Expresando esta ecuación en su forma canónica, queda:
1
9364
222
zyx
de donde se desprende que:
2a
,
3c

UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 39
Además, el signo negativo en el término que contiene a la variable y nos indica que el eje de
este hiperboloide de una hoja es precisamente el eje y.
Su representación gráfica es:
C- Consideremos ahora el caso en que dos de los coeficientes de la ecuación
RPzNyMx
222
son negativos y otro positivo.
Sean por ejemplo,
;00,0 PyNM
y dividimos toda la ecuación por R.
1
222
P
R
z
N
R
y
M
R
x
Esta vez tendremos que:
2
a
M
R
;
22
; c
P
R
b
N
R
por lo que la ecuación queda en la forma:
1
2
2
2
2
2
2
b
y
a
x
c
z

UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 40
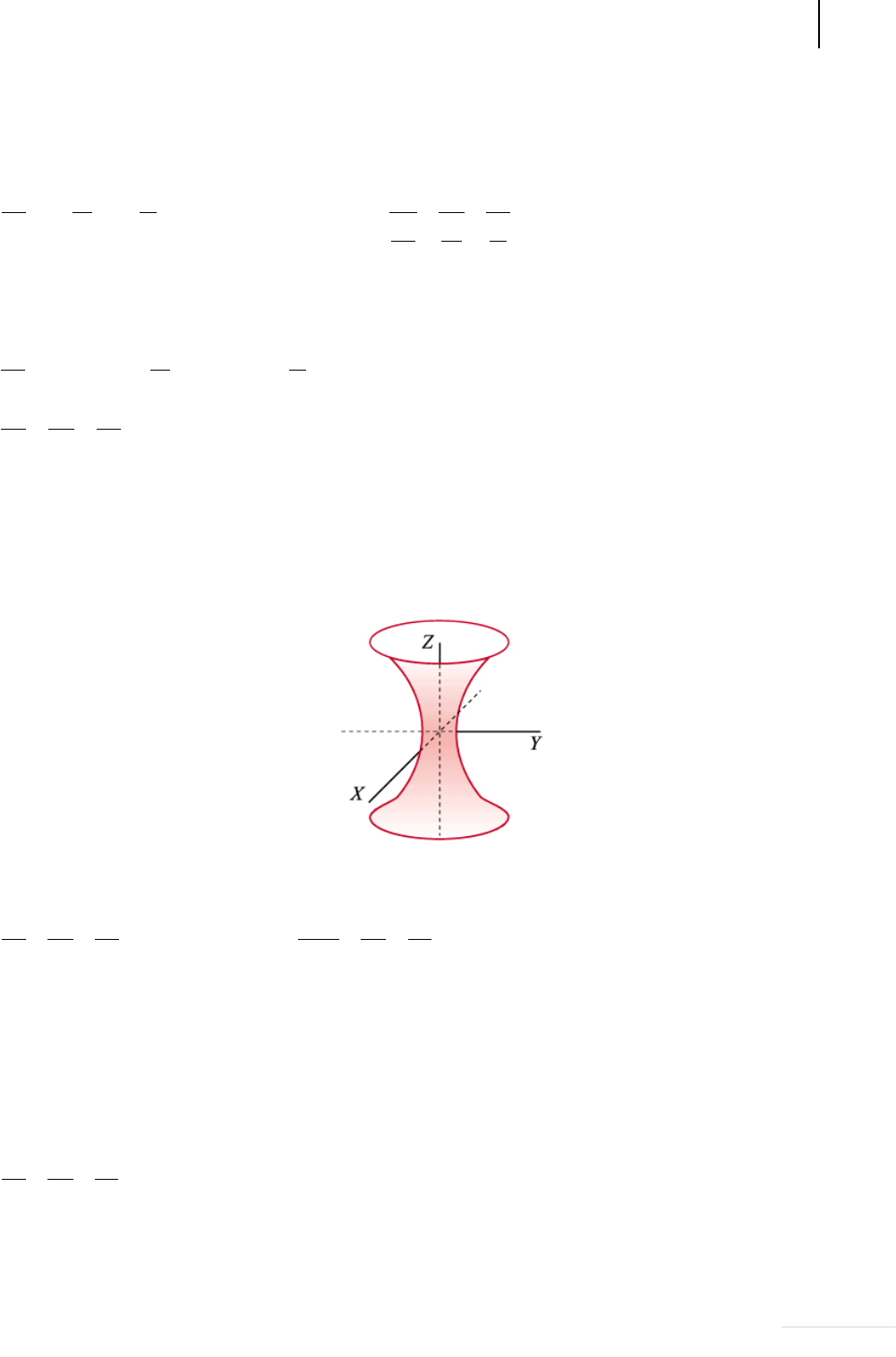
Esta es la forma canónica de la ecuación de una superficie llamada HIPERBOLOIDE DE
DOS HOJAS; la cual posee las siguientes características: sólo intercepta al eje z, en dos
puntos de coordenadas
coo ,,
; es simétrica respecto al origen de coordenadas, a los ejes y
planos coordenados; es abierta puesto que las variables x e y pueden tener cualquier valor
real y la variable z cumple con que
cz
, secciones planas paralelas al plano xy dan elipses,
excepto para
ccz ;
, mientras que secciones planas paralelas a los restantes planos
coordenados dan hipérbolas .
Otras formas canónicas de la ecuación del hiperboloide de dos hojas son :
11
2
2
2
2
2
2
2
2
2
2
2
2
c
z
a
x
b
y
c
z
b
y
a
x
los que poseen características semejantes a las descriptas anteriormente, pero tienen su eje
coincidiendo en el eje x y el eje y respectivamente, por aparecer en su ecuación la variable
que se mide sobre éstos ejes con coeficientes positivos.
Ejemplo: Representar el hiperboloide de dos hojas que responde a la ecuación:
11216167
222
zyx
Primeramente llevemos la ecuación a la forma canónica dividiendo por 112.
1
7716
222
zyx
Su intercepto con el eje x es el punto cuyas coordenadas son
0,0,4
.
El signo positivo del coeficiente de la variable x nos indica que el eje del hiperboloide es
precisamente el eje x; los signos negativos en las otras dos variables nos sirven para
identificar que se trata de un hiperboloide de dos hojas. Su representación gráfica es :
Se puede observar en la representación gráfica que hemos alterado la posición de los ejes , lo
que es permisible siempre que se conserve el sentido de la rotación. Esto nos posibilita dibujar
la superficie en la posición de más fácil visualización en tres dimensiones
CUADRICAS NO CENTRADAS
Tomemos ahora la ecuación:
SzNyMx
22
(1)
Correspondiente a las cuádricas que hemos llamado NO CENTRADAS.
Supongamos
0S
A- Si los coeficientes M y N son ambos positivos, es decir en el caso que :
0,0 NM
y
z
x
(4,0,0)
(-4,0,0)

UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 41
Dividiendo la ecuación (1) por S:
zy
S
N
x
S
M
22
y pasamos los coeficientes de las variables x e y al denominador:
z
N
S
y
M
S
x
22
de acuerdo al signo de S, se tiene :
z
b
y
a
x
2
2
2
2
(2) en donde
22
b
N
S
ya
M
S
De la observación de la ecuación (2) se deduce que esta cuádrica tiene dos planos de simetría
(los planos xz e yz ) llamados PLANOS PRINCIPALES, y un eje de simetría (eje z ) ,
llamado EJE PRINCIPAL y que carece de centro de simetría .
Su único intercepto es el origen de coordenadas.
La superficie es abierta puesto que las variables x e y pueden tomar cualquier valor real,
mientras que la variable z está restringida a
R
o a
R
según sea el signo de S (positivo o
negativo respectivamente). De ahí que la superficie se extenderá por encima o por debajo del
plano xy según S 0 ó S 0.
Sus secciones planas paralelas al plano xy son elipses, mientras que las secciones planas
paralelas a los restantes planos coordenados son parábolas.
Tal superficie recibe el nombre de PARABOLOIDE ELIPTICO.
Su representación gráfica para S 0 es:
Otras formas canónicas posibles de la ecuación de un paraboloide elíptico son:
y
c
z
a
x
x
c
z
b
y
2
2
2
2
2
2
2
2
Que tendrán propiedades similares a las descriptas anteriormente pero que sus ejes principales
son respectivamente, x e y.
Ejemplo: Representar el paraboloide elíptico cuya ecuación es :
oyzx 44
22
Llevemos la ecuación dada a la forma canónica, para ello debemos transponer al 2° miembro
el término lineal.

UNIVERSIDAD NACIONAL DEL CHACO AUSTRAL
GEOMETRÍA EN EL ESPACIO: Superficies cuádricas
11
INGENIERIA: QUIMICA, ALIMENTOS, INDUSTRIAL, SISTEMAS DE INFORMACIÓN: Álgebra Lineal y Geometría
Analítica
FARMACIA: Matemática II
PROFESORADO EN CIENCIAS QUIMICAS Y DEL AMBIENTE: Álgebra y Geometría Analítica
PROFESORADO EN FISICA: Álgebra y Geometría Analítica
PROFESORADO EN MATEMATICA: Álgebra Lineal y Geometría
Página | 42
yzx 44
22
dividiendo por -4 resulta
y
zx
41
22
Analizando esta ecuación llegamos a la conclusión de que el paraboloide tiene como eje
principal al eje y, y que el mismo se desarrolla sobre el semieje negativo de este eje.
Su representación gráfica es:
B- Analicemos a continuación el caso en que M y N posean signos contrarios en la ecuación.
Sea por ejemplo;
00 NyM
, y puesto que
0S
dividamos toda la ecuación por
él:
z
N
S
y
M
S
x
22
Atendiendo a los signos de los coeficientes tenemos:
22
b
N
S
ya
M
S
por lo que la ecuación queda en la forma:
z
b
y
a
x
2
2
2
2
(3)
Del análisis de la ecuación (3) se desprende que la cuádrica tiene dos planos de simetría (los
planos
xz
y
yz
) y un eje de simetría (eje z) y carece de centro de simetría.
Solamente tiene un intercepto con los ejes coordenados: el origen, la superficie es abierta
puesto que las tres variables pueden tomar cualquier valor real. Las secciones planas paralelas
a
xy
son hipérbolas con ecuaciones de la forma:
kzk
b
y
a
x
,
2
2
2
2
Sus trazas sobre este plano se obtienen haciendo
0k
, en la que se determinan las rectas:
0,0 z
b
y
a
x
0,0 z
b
y
a
x
z
x
y
O
Este documento contiene más páginas...
Descargar Completo
14 Superficies Cuádricas.pdf
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.