
Física e Introducción a la Biofísica
1
Apunte de Cátedra
Unidad 1. Introducción a la biomecánica
En esta Unidad analizaremos las leyes y principios que nos permitirán avanzar en el
conocimiento de las fuerzas y las aceleraciones que actúan sobre los organismos
vivos, lo que conocemos como biomecánica.
Los
contenidos que se tratarán son:
Concepto de masa, tiempo y espacio.
Sistema de Unidades: Sistema Internacional de Unidades (SIU) y
Cegesimal.
Cinemática: concepto de velocidad. Movimiento rectilíneo uniforme.
Concepto de aceleración. Movimiento uniformemente variado.
Aceleración de la gravedad. Tiro vertical y caída libre. El principio de
inercia. Fuerza: concepto general, unidades. Principio de acción y
reacción. Trabajo y Energía. Potencia.
A diario decimos o escuchamos expresiones tales como:
¡Qué veloz es un halcón!
¡Acelerá que llegamos tarde!
¡Empujen con más fuerza!
¡Qué trabajo me dio!
Sin embargo, nunca nos preguntamos cuál es el significado físico de cada una de
estos términos.
El recorrido de esta unidad propone conocer muchos de los conceptos que nos
permitirán analizar si estas expresiones tan comunes están correctamente
formuladas.

Física e Introducción a la Biofísica – UBA XXI - Primer cuatrimestre 2017
Cinemática
La cinemática es una parte de la mecánica que se dedica al estudio de los
cuerpos en movimiento, sin considerar las causas que lo producen o modifican.
El objeto de la mecánica es describir movimientos de cuerpos y el lenguaje
empleado para describir en forma adecuada y precisa dichos movimientos es la
cinemática.
En este documento desarrollaremos las técnicas básicas para la descripción de
movimientos de cuerpos sobre trayectorias rectilíneas.
Como toda disciplina científica, la cinemática comienza con una serie de
convenciones o acuerdos que son los que finalmente otorgan significación universal
a sus conclusiones.
Cuando la posición de un cuerpo puntual cambia respecto a un observador a
medida que transcurre el tiempo podemos afirmar que ese cuerpo está en
movimiento respecto a ese observador.
A ése cuerpo puntual solemos llamarlo
“móvil”, mientras que a ése observador
que percibe el movimiento del móvil solemos llamarlo “sistema de referencia”.
Podemos explicitar algunas ideas que están implícitas dentro del párrafo anterior y
que son inherentes a la propia definición de movimiento.
La
posición es el lugar donde está el cuerpo en un instante determinado,
independientemente de si esa posición o ese instante son valores conocidos,
o no, a la hora de afrontar un problema.
Podemos saber o no saber en qué posición se encuentra un móvil en un
determinado instante respecto a un observador, pero, lo que no podemos
tener dudas es que en cada instante sucesivo el móvil podrá estar en una y
sólo una posición respecto a ese observador.
Un mismo objeto puede estar en reposo respecto a un observador de
referencia, y simultáneamente estar en movimiento respecto a otro
observador de referencia diferente.
(Cuando usamos la expresión “estar en reposo respecto a un observador”
queremos decir que el cuerpo está quieto respecto a ese sistema de
referencia).
Por ejemplo, si Ana espera en el andén de una estación de ferrocarriles un
tren, del que bajarán sus amigas Beatriz y Cecilia, Ana puede decir que
Beatriz y Cecilia se están moviendo respecto a ella porque ambas están
ocupando posiciones cada vez más cercanas a ella a medida que transcurre
el tiempo.
De la misma manera también Beatriz y Cecilia podrían decir que Ana se
mueve con respecto a ellas porque, desde el punto de vista de ellas, Ana va
ocupando posiciones cada vez más cercanas a ellas a medida que transcurre
el tiempo.
Sin embargo, si Beatriz y Cecilia viajan sentadas una frente a la otra, o una
al lado de la otra, ambas dirán que están quietas una respecto a la otra.

Apunte de Cátedra: Introducción a la biomecánica – Física e Introducción a la Biofísica – UBA
XXI
3
Una situación como la anteriormente detallada solemos describirla de la
siguiente forma (notar que llamaremos a cada mujer por la inicial de su
nombre).
A está en movimiento respecto a B.
A está en movimiento respecto a C.
B está en movimiento respecto a A.
B está en reposo respecto a C.
C está en movimiento respecto a A.
C está en reposo respecto a B
Por último, cabe agregar que esta situación planteada para las tres mujeres
es mucho más frecuente que lo que notamos percibirlo dado que no sólo
ocurre cuando observamos o viajamos en un tren, auto, avión, barco, etc.
sino que además aún cuando no hagamos referencia a ningún medio de
transporte todos nosotros estamos “viajando” en un planeta que se mueve
respecto al Sol, el cual se mueve respecto al centro de la galaxia Vía Láctea,
la cual a su vez se mueve respecto a otras galaxias vecinas incluso aún
cuando nos encontremos en reposo respecto a la silla en la que estemos
sentados.
Es muy importante darnos cuenta que no tiene ningún sentido físico
decir que un cuerpo está en reposo o en movimiento si no vamos a
explicitar respecto a qué sistema de referencia lo estamos
analizando.
En resumen, podemos decir que:
el movimiento es el cambio de posición de un cuerpo, respecto a un
punto considerado fijo, a medida que pasa el tiempo.
Para definir si el cuerpo está en movimiento o en reposo, debemos preguntarnos:
¿Dónde está? y
¿Cuándo está en esa posición?
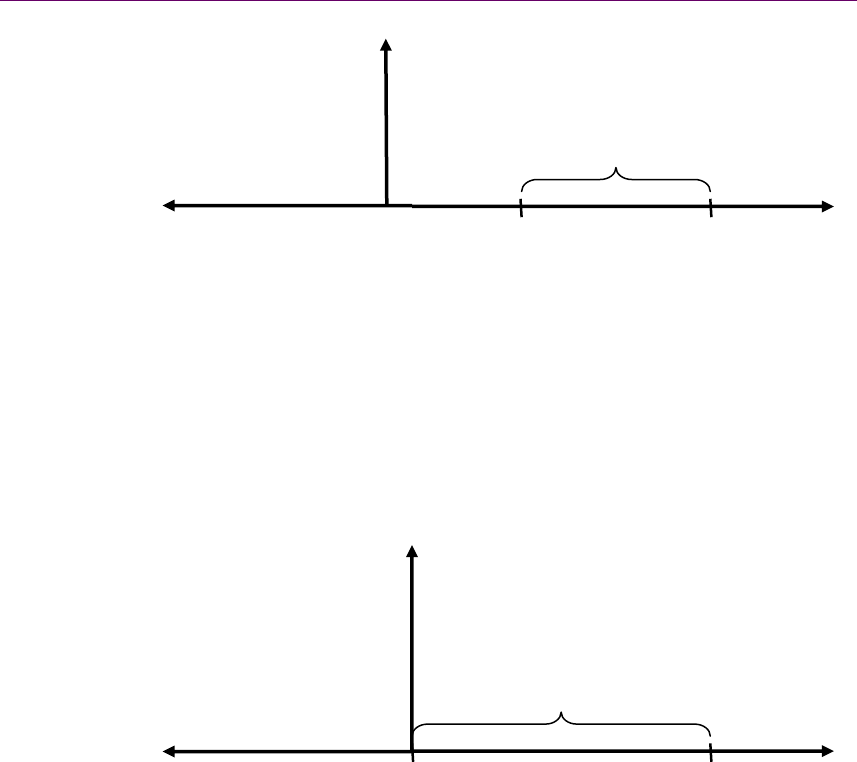
Es decir, es necesario informar la posición que ocupa y el instante en el que la
ocupa. Para esto debemos construir un sistema de referencia, tomando un par de
ejes
x e y. En el 0 de x ubicamos el punto de referencia desde donde tomaremos la
distancia de la posición del cuerpo. Por ejemplo, si decimos que un caballo está a
10 metros de la tranquera, debemos ubicar la tranquera en el punto 0 del eje x.

Física e Introducción a la Biofísica – UBA XXI - Primer cuatrimestre 2017
Si el caballo se desplaza, tendríamos que ubicar la nueva posición en el eje x, pero
siempre respecto al 0 (tranquera).
Como se puede inferir del gráfico de arriba, existen posiciones negativas, que
indican la posición de otro cuerpo “por detrás” del punto de referencia. Si en el
ejemplo anterior aparece otro caballo del otro lado de la tranquera, a 5 metros, lo
ubicaríamos de la siguiente manera.
Entonces diremos que el nuevo caballo se encuentra a -5 metros de la tranquera.
Como vemos, existen posiciones positivas y negativas.
Desplazamiento
Es el espacio recorrido por un cuerpo, cuando pasa de una posición a otra. Si el
caballo 1 que estaba en la posición 10 metros se aleja hasta 25 metros de la
tranquera, se desplazó 15 metros. Se representa matemáticamente de la siguiente
manera:
X
0
= posición inicial (donde estaba el caballo)
X
1
= posición final (donde llegó el caballo)
ΔX = espacio recorrido.
ΔX = (X
1
– X
0
)
ΔX = 25 m – 10 m = 15 m
Apunte de Cátedra: Introducción a la biomecánica – Física e Introducción a la Biofísica – UBA
XXI
5
ΔX
0 X
0
10 m x
1
25 m
tranquera caballo 1
Supongamos ahora que el caballo uno (c
1
) avanza hacia la tranquera, y que en
un instante posterior llega a la tranquera. La nueva posición del caballo
coincide con la de la tranquera, tenemos entonces que:
ΔX
x
1
0 m X
0
25 m
tranquera caballo 1
Notemos que el desplazamiento del caballo uno nos ha dado negativo porque
precisamente ha avanzado hacia la izquierda (hacia donde habíamos llamado
negativo) y no hacia la derecha.
Tiempo transcurrido
El intervalo de tiempo Δt es el tiempo que el caballo estuvo
moviéndose. Si a las 8 horas estaba en la posición X
0
y a las 8 hs y
10 s en X
1
, el tiempo que estuvo moviéndose fue de 10 segundos. Se
expresa matemáticamente de la siguiente manera: t = t
1
– t
0

Física e Introducción a la Biofísica – UBA XXI - Primer cuatrimestre 2017
t
0
t
t
1
0 10 m 25 m
tranquera X
0
caballo 1 X
1
Velocidad
Supongamos que el caballo 1 se aleja de la tranquera al trote, la rapidez con que se
mueve es la velocidad. Podemos definir a la velocidad como:
el espacio o distancia recorrida en cada unidad de
tiempo. También se puede definir como el cociente entre
la distancia recorrida y el tiempo empleado en recorrerla.
Su expresión matemática es:
donde:
v = velocidad
x= espacio recorrido
t = tiempo
Si el caballo 1 se desplaza 15 metros en 10 segundos, alejándose de la tranquera,
es decir en el sentido del eje x, su velocidad será positiva (+ 1,5m/s). En cambio, sí
se mueve en sentido contrario, hacia la tranquera, la velocidad será negativa (-1,5
m/s).

Apunte de Cátedra: Introducción a la biomecánica – Física e Introducción a la Biofísica – UBA
XXI
7
1. Movimiento rectilíneo uniforme (MRU)
Comencemos con un ejemplo: si observamos un auto por una autopista rectilínea
que recorre en el primer minuto 2 kilómetros, en el segundo minuto 2 kilómetros y
en el tercer minuto otros dos kilómetros, diremos que se está desplazando en
forma uniforme.
Movimiento rectilíneo uniforme es aquel en el cual el
cuerpo describe una trayectoria rectilínea y recorre
espacios iguales en tiempos iguales. La velocidad es
constante.
Si la velocidad del móvil varía, decimos que tiene aceleración.
En el caso del MRU la velocidad permanece constante, por lo tanto la
aceleración media es nula (vale cero).
La aceleración media indica cuál es la proporción con la que se va modificando la
velocidad de un cuerpo en movimiento a medida que transcurre el tiempo.
Habíamos visto en el ejemplo anterior que el caballo se desplazó de un punto a otro
en un determinado tiempo. Dichos cambios podemos representarlos en una tabla
de la siguiente manera:
Con esta tabla construimos un gráfico. Para cada valor de tiempo le corresponde
una posición.
X (m)
40
25
10
0 10 20 t (s)
Este gráfico es la representación del cambio de posición en función del
tiempo. El valor 10 m corresponde al valor de la posición en el tiempo 0, o sea la
posición inicial X
0.
Con este gráfico podemos calcular la posición en cualquier tiempo
que tomemos.
También podemos graficar la velocidad y la aceleración en función del tiempo.

Física e Introducción a la Biofísica – UBA XXI - Primer cuatrimestre 2017
v (m/s)
1,5
10 20 t (s)
Gráfico de velocidad en función del tiempo. Velocidad constante.
a (m/s
2
)
t (s)
Gráfico de aceleración en función del tiempo a = 0
1.1. Ecuaciones horarias del movimiento rectilíneo uniforme
La definición de velocidad que vimos en este documento, se representa
matemáticamente de la siguiente manera:
v = X
f
– X
0
t
f
- t
0
Si despejamos X
f
– X
0
queda:
v . (t – t
0
) = X – X
0
X = X
0
+ v . (t
F
– t
0
) Ecuación horaria
Esta ecuación nos permite calcular a qué distancia se encontrará el cuerpo en
movimiento en un determinado tiempo. En el caso del caballo podemos ver a qué
distancia de la tranquera se encuentra luego de un minuto de trote.
X = 10 m + 1,5 m/seg . (60 seg – 0seg)
X = 10 m +1,5 m/seg . 60 seg
X = 10 m + 90 m

Apunte de Cátedra: Introducción a la biomecánica – Física e Introducción a la Biofísica – UBA
XXI
9
X = 100 m
Para la velocidad su ecuación horaria será:
v = constante
Para la aceleración:
a = 0
2. Movimiento rectilíneo uniformemente variado
(MRUV)
Hasta ahora vimos cómo el caballo se alejaba de la tranquera a una velocidad
constante, pero qué sucede si ese caballo está asustado y comienza a alejarse de
la tranquera cada vez más rápido. Supongamos que esto ocurre en la realidad,
aunque no es tan exacto. Primero a 1,5 m/s, luego a 3m/s, luego 4,5 m/s, y así va
aumentando. Vemos que su velocidad va variando en forma uniforme, por cada
segundo su velocidad aumenta 1,5 m/s. Esta situación es la que definimos como
movimiento uniformemente variado, la velocidad cambia lo mismo en cada
segundo.
Si lo queremos expresar en forma matemática diremos que:
Δv = 1,5m/s en cada Δt = 1 segundo
Nuevamente vemos el concepto de aceleración, el caballo fue aumentando su
velocidad con el tiempo, es decir tuvo una aceleración evidente. A la aceleración la
podemos expresar matemáticamente así:
a =
a =
a =
a = =
a = 1,5 m/s
2

Física e Introducción a la Biofísica – UBA XXI - Primer cuatrimestre 2017
Este valor nos indica que la aceleración del caballo es tal que su velocidad aumenta
1,5 metro por segundo, en cada segundo que pasa.
En el movimiento uniformemente variado la aceleración es constante, es decir
que en el MRUV la velocidad aumenta todo el tiempo (o disminuye todo el tiempo).
Y que esa variación de velocidad es lineal con el tiempo.
La aceleración puede tener signo positivo o negativo, veamos cómo puede ser:
Si el caballo fuera disminuyendo su velocidad de 3m/s a 1,5 m/s por cada segundo
que pasa, la ecuación sería esta:
a =
a =
a = =
a = - 1,5 m/s
2
2.1. Ecuaciones horarias y gráficos del MRUV
Como vimos anteriormente, las ecuaciones horarias corresponden a las de posición,
velocidad y aceleración en función del tiempo.
a) Ecuación horaria para la aceleración (a = f(t) )
La característica fundamental de un movimiento uniformemente variado es que la
aceleración es constante, no cambia. Su expresión matemática es:
a = constante
En forma gráfica, la representamos así:
a (m/s
2
)
t (s)
b) Ecuación horaria para la velocidad (v= f (t))
Si decimos que la aceleración es constante, decimos también que la velocidad
aumenta (o disminuye) linealmente con el tiempo.
Recordemos la definición de aceleración a través de su representación matemática:

Apunte de Cátedra: Introducción a la biomecánica – Física e Introducción a la Biofísica – UBA
XXI
11
a =
a =
si despejamos:
v
f
– v
0
= a . (t
f
– t
0
)
v
f
= v
0
+ a . (t
f
– t
0
)
Si el tiempo inicial, habitualmente, vale cero, la ecuación de la velocidad queda así:
v
f
= v
0
+ a . t
El gráfico de la ecuación horaria de la velocidad es el que sigue:
v (m/s)
v
0
t (s)
Si recordamos la ecuación de la recta es:
y = m.x + b
Este gráfico corresponde a una función lineal (recta), donde la pendiente
m es la
aceleración, la variable independiente
x es el tiempo, la variable dependiente y es
la velocidad y la ordenada al origen b corresponde a la velocidad inicial v
0
.

Física e Introducción a la Biofísica – UBA XXI - Primer cuatrimestre 2017
c) Ecuación horaria de la posición en función del tiempo (x = f(t) )
X = X
0
+ v
0
t + ½ a t
2
Si la ecuación de la parábola o cuadrática es y = a x
2
+ b x + c, podemos
relacionar cada término de la ecuación X = X
0
+ V
0
t + ½ a t
2
con su equivalente en
la parábola:
X
0
---------- c
v
0
.t--------- b.x
½ a t
2
------- a.x
2
La representación de la posición en función del tiempo es:
Este gráfico representa la variación de la posición en función del tiempo para un
movimiento uniformemente variado. Es la representación gráfica de la función:
X = X
0
+ v
0
t + ½ a t
2
.
Retomando el ejemplo del caballo, a través de esta ecuación podemos conocer su
posición para cualquier instante t. Por ejemplo, si queremos saber a qué distancia
se encontrará el caballo luego de 10 segundos, manteniendo las mismas
condiciones de aceleración, debemos hacer el siguiente cálculo:
X = X
0
+ v
0
t + ½ a t
2
X = 10 m + 1,5 m/s . 10 s + ½ . 1.5 m/s
2
. (10 s)
2
X = 10 m + 15 m + ½ . 1,5 m/s
2
. 100 s
2
X = 25 m + 75 m
X = 100 m

Apunte de Cátedra: Introducción a la biomecánica – Física e Introducción a la Biofísica – UBA
XXI
13
Si queremos saber qué velocidad tendrá en ese tiempo, debemos recordar la
ecuación horaria de la velocidad:
v
f
= v
0
+ a . t
v
f
= 1,5 m/s + 1.5 m/s
2
. 10 s
v
f
= 1,5 m/s + 15 m/s
v
f
= 16,5 m/s
Si la expresamos en km/h, la velocidad será:
En 1 s ……………………… 16,5 m
En 3.600 s ………………. 59.400 m
1.000 m……………….. 1 km
59.400 m/h……………… 59,4 km/h
Al recopilar todo lo visto es posible establecer que,
a los 10 segundos de iniciada
su carrera, el caballo estará a 100 metros de la tranquera, corriendo a una
velocidad de 59,4 km/h.
Si un cuerpo parte del reposo y de una posición X
0
igual al punto de que tomamos
de referencia (X
0
= 0) la ecuación cuadrática queda:
X = X
0
+ v
0
t + ½ a t
2
X = ½ a t
2
Retomando todo lo hasta aquí desarrollado, resultan las siguientes afirmaciones:
En un movimiento uniformemente variado la
aceleración es constante.
En la fórmula v
f
= a. t, siendo a constante, resulta que
la velocidad en un movimiento uniformemente variado
es directamente proporcional al tiempo.
En la expresión de posición (espacio recorrido) X = ½
a t
2
, siendo a constante, resulta que el espacio
recorrido con movimiento rectilíneo uniformemente
variado es directamente proporcional al cuadrado del
tiempo.

Física e Introducción a la Biofísica – UBA XXI - Primer cuatrimestre 2017
3. Caída libre y tiro vertical
La observación de los eventos diarios, nos indican que todo cuerpo librado a la
acción de su peso cae debido a que actúa sobre él la fuerza de atracción de la
gravedad. Desde la antigüedad, este fenómeno atrajo la atención de los científicos.
Al principio se pensaba que cuando más pesado era un cuerpo, mayor era la
velocidad con que llegaba a la tierra, más rápido llegaba al piso. Galileo Galilei fue
el primero en demostrar lo erróneo de ese pensamiento. Con su conocida
experiencia, en la cual dejó caer tres cuerpos de diferente peso cada uno, pero de
igual forma y tamaño, demostró que los tres llegaban al suelo simultáneamente. Es
evidente que si dejamos caer un papel y una piedra, no llegan al piso al mismo
tiempo. La diferencia resulta como consecuencia del rozamiento del aire con los
cuerpos. Gracias a esta demostración, Galileo emitió el siguiente enunciado que se
conoce como
Ley de la caída en el vacío:
Todos los cuerpo que caen desde la misma altura,
adquieren en el vacío (prescindiendo del rozamiento del
aire) la misma velocidad.
Todo cuerpo que soltemos caerá con una aceleración de 9,8 m/s
2
. Si suponemos
que no hay resistencia del aire, todos los cuerpos caerán con la misma aceleración,
que se conoce como aceleración de la gravedad. Se la denomina con la letra g y
siempre apunta hacia el centro de la Tierra.
Si todos los cuerpos al caer en un mismo lugar desde la misma altura, adquieren la
misma velocidad y llegan simultáneamente al suelo, podemos afirmar que todos
tienen la misma aceleración. Si esto es así, acabamos de deducir que la caída de los
cuerpos es un movimiento uniformemente variado, por lo tanto se cumplen las
mismas leyes.
En el MRUV los cuerpos se movían en sentido del
eje X (horizontal) con una
aceleración que llamamos a y vimos que las ecuaciones horarias para el MRUV
eran:
X = X
0
+ v
0
t + ½ a t
2
v
f
= v
0
+ a . (t
f
– t
0
)
En el caso de la caída libre los cuerpos se mueven en sentido del
eje Y (vertical) y
la aceleración es la correspondiente a la gravedad y la representamos con la letra
g. Para caída libre, las ecuaciones horarias serán entonces:
Y = Y
0
+ v
0
t + ½ g t
2
v
f
= v
0
+ g . (t
f
– t
0
)

Apunte de Cátedra: Introducción a la biomecánica – Física e Introducción a la Biofísica – UBA
XXI
15
Por ejemplo, si una paloma tiene su nido en una rama a 10 metros del suelo y por
accidente se cae un huevo al piso. ¿Cómo podemos calcular la velocidad final y
cuánto tardó en llegar al piso?
Y
nido 10 m
0
La velocidad inicial (v
0
) es 0 y la posición final Y será 0, ya que es el origen de la
recta Y.
Si reemplazamos en la ecuación queda:
Y = Y
0
+ v
0
t + ½ g t
2
0 = 10 m – ½ . 9.8 m/s
2
. t
2
4,9 m/s
2
. t
2
= 10 m
t
2
= 10 m
4,9 m/s
2
t =
t = 1,43 s
El huevo tardó 1,43 segundos en llegar al piso ¿con qué velocidad final?
Si reemplazamos este tiempo en la segunda ecuación, tendremos la velocidad con
que llega al piso. Recordemos que v
0
= 0
v
f
= v
0
+ g . (t
f
– t
0
)
v
f
= - 9,8 m
. 1,43 s
s
2
v
f
= - 14 m/s
El signo negativo de v
f
indica que la velocidad va en sentido contrario al eje y. Si lo
queremos pasar a km/h nos dará que la velocidad de impacto contra el suelo fue de
50,4 km/h. ¿Se habrá roto el huevo?
En el caso del
tiro vertical es el movimiento contrario a la caída libre. Es cuando
lanzamos un cuerpo hacia arriba y en forma vertical, prescindiendo del rozamiento
del aire. El cuerpo arrojado sale con una velocidad inicial y se va frenando hasta
Este documento contiene más páginas...
Descargar Completo
6) Rivolta, M. y Benavides, L. (2017), Apunte de cátedra Unidad 6. Introducción al manejo de señales en los seres vivos.pdf
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Descargar
 Estamos procesando este archivo...
Estamos procesando este archivo...
 Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.
Lamentablemente la previsualización de este archivo no está disponible. De todas maneras puedes descargarlo y ver si te es útil.